A static analysis setting (SA) specifies the rules according to which load cases and load combinations are calculated.
Analysis Types
In RFEM and RSTAB, three standard analysis types are preset:
- Geometrically Linear
When calculating according to the geometrically linear analysis (first-order), the equilibrium is analyzed on an undeformed structural system.
- Second-Order
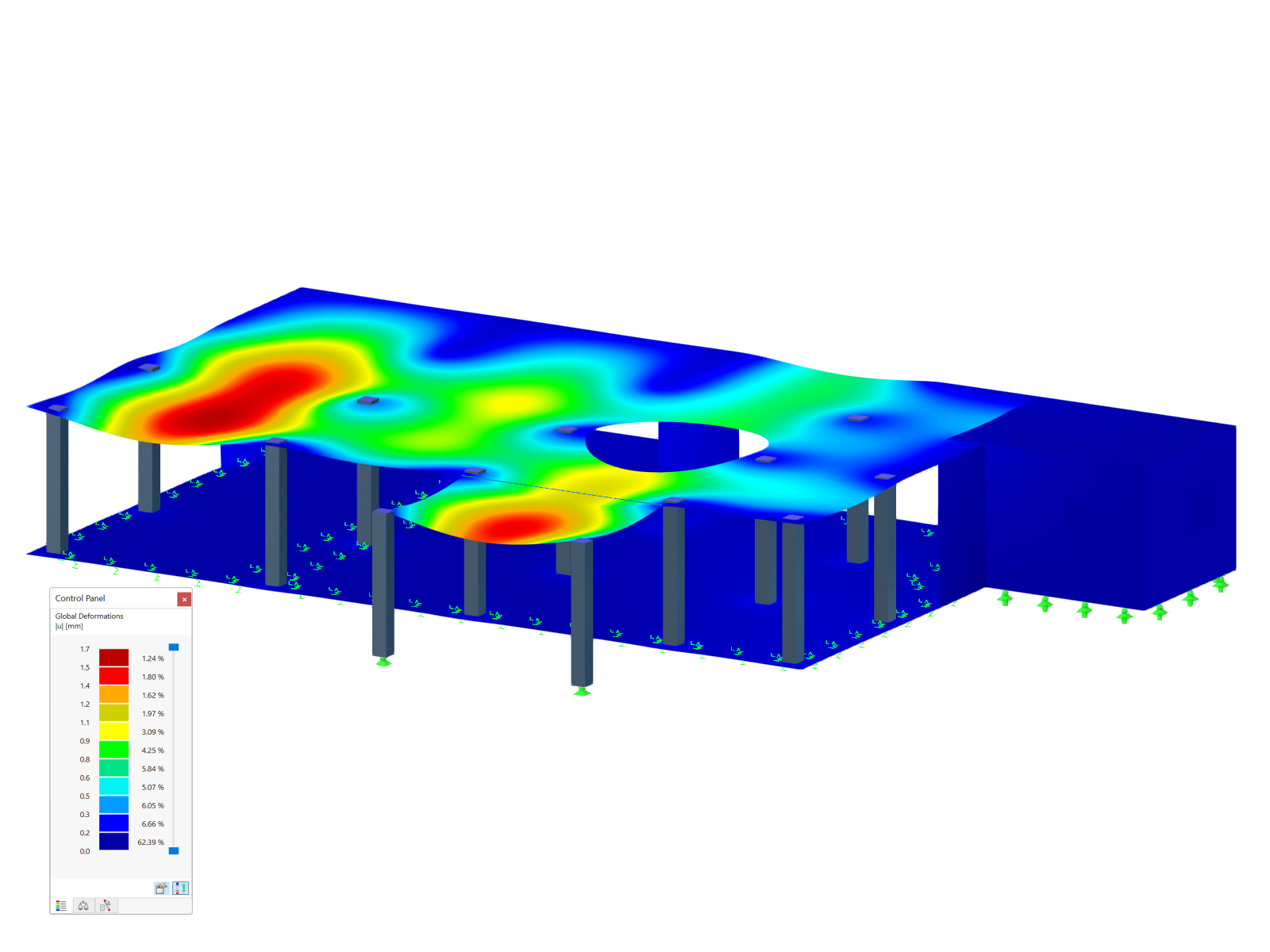
In the "structural" second-order analysis, the equilibrium is determined on a deformed structural system. Deformations are assumed to be small.
- Large Deformations
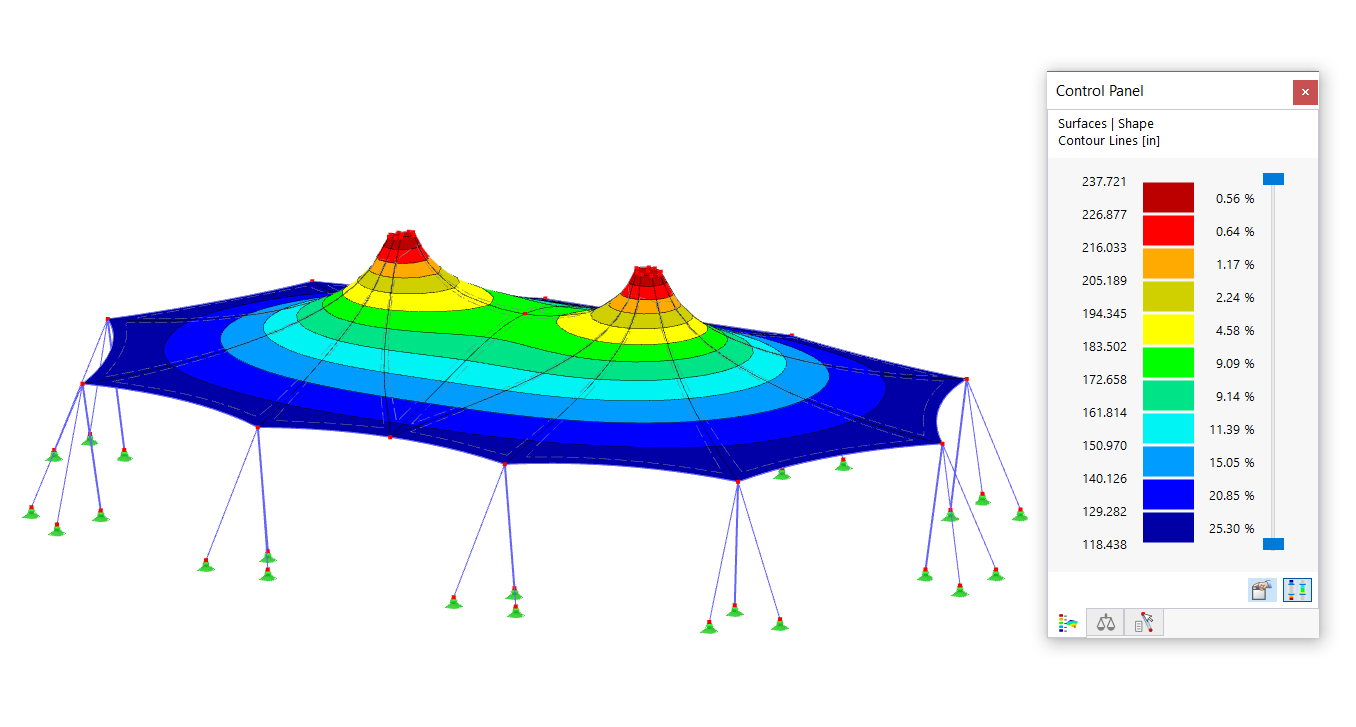
The large deformation analysis (third-order or theory of large deformations) considers longitudinal and transversal forces in the calculation. After each iteration step, the stiffness matrix of a deformed system is created.
Iterative method for nonlinear analysis
Depending on the analysis type, various methods are available to solve the nonlinear algebraic system of equations.
- Newton-Raphson
The approach according to Newton-Raphson is preset for the large deformation analysis. The nonlinear equation system is solved numerically by means of iterative approximations with tangents.
- Picard
The method according to Picard, also known as the secant method, can be understood as a finite-difference approximation of the Newton-Raphson method. The difference between the current and the original iteration run in the current load increment step is considered.
- Newton-Raphson Combined with Picard
The approach according to Picard is applied first. After a few iterations, a switch is made to the Newton-Raphson method.
- Newton-Raphson with Postcritical Analysis
This method is suitable for solving post-critical analyses where an area with instability has to be overcome.
- Dynamic Relaxation
The final method is suitable for calculations according to the large deformation analysis and for solving problems regarding the post-critical issues. In this approach, an artificial time parameter is introduced. Taking into account inertia and damping, the failure can be handled as a dynamic problem.
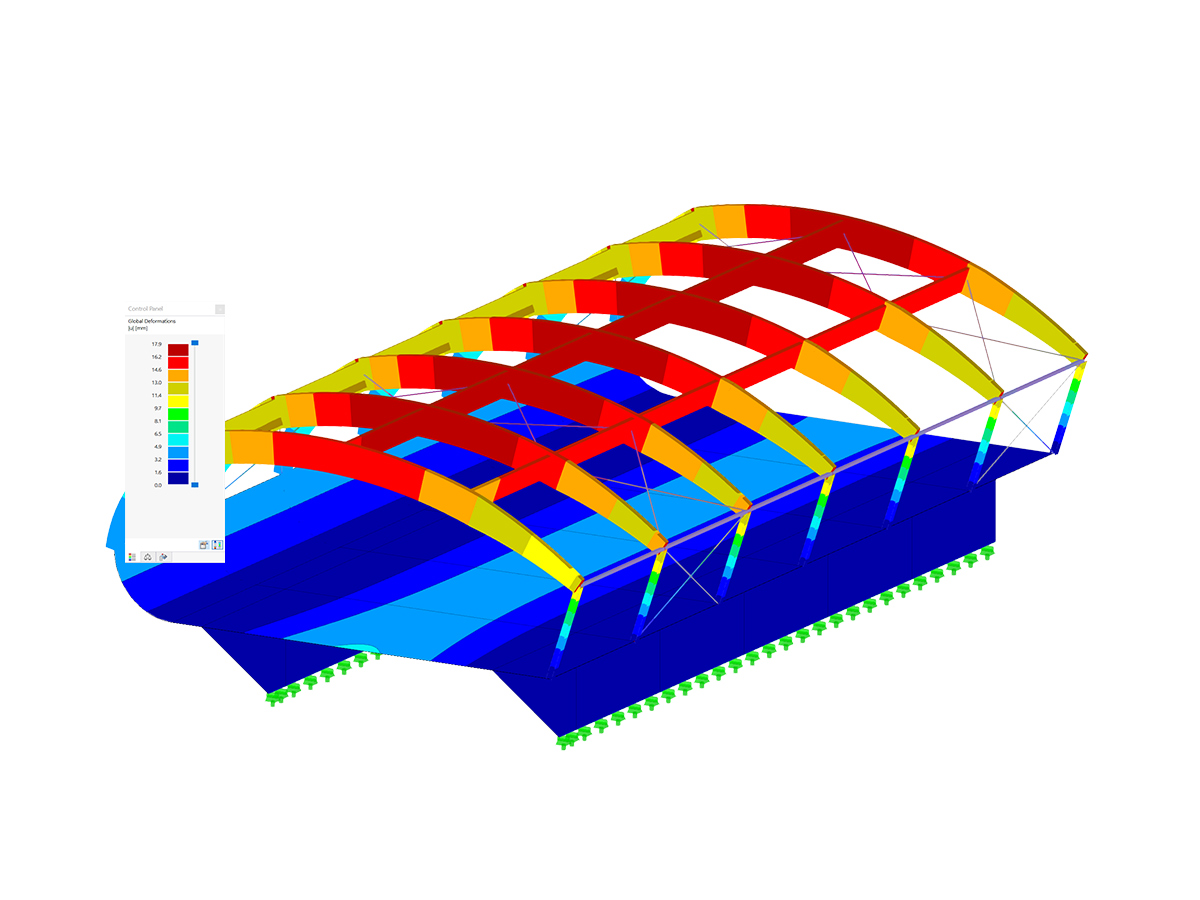
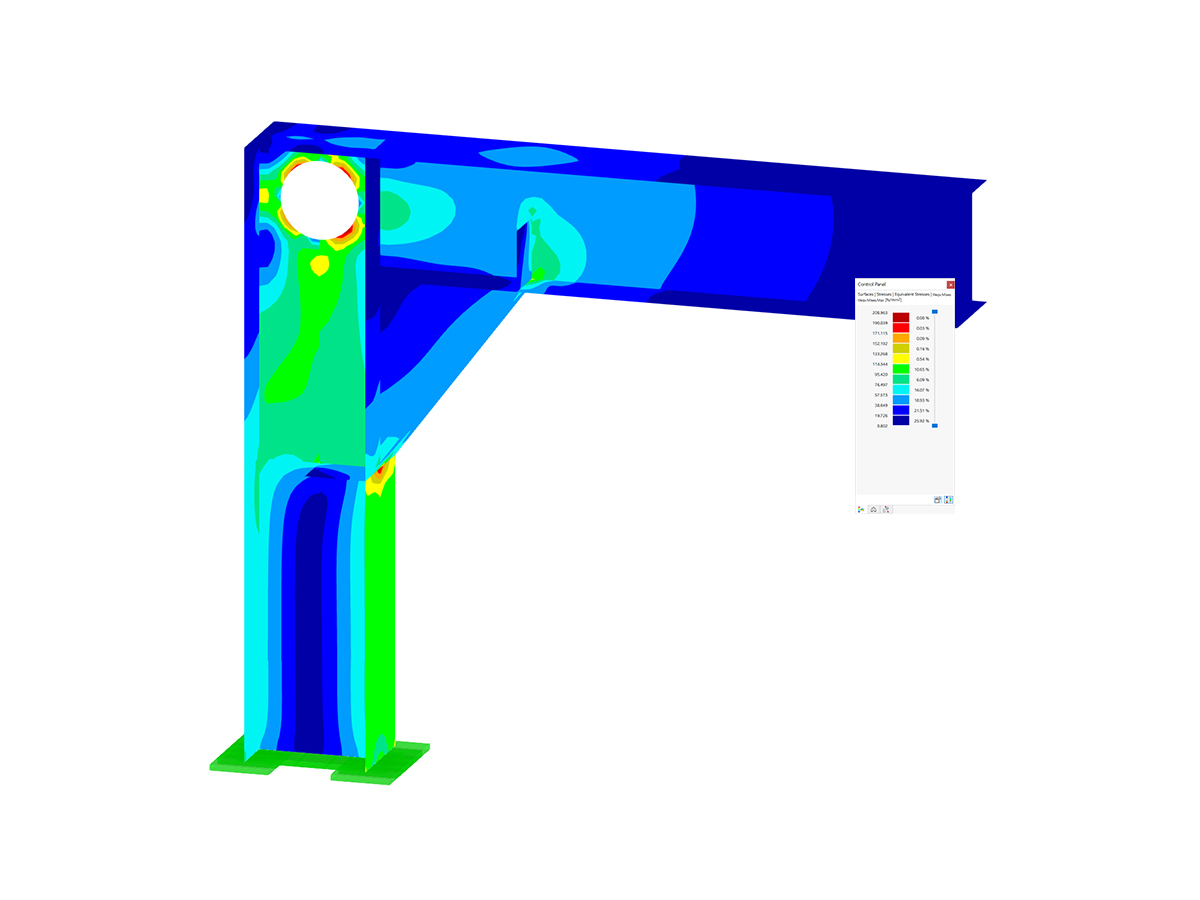
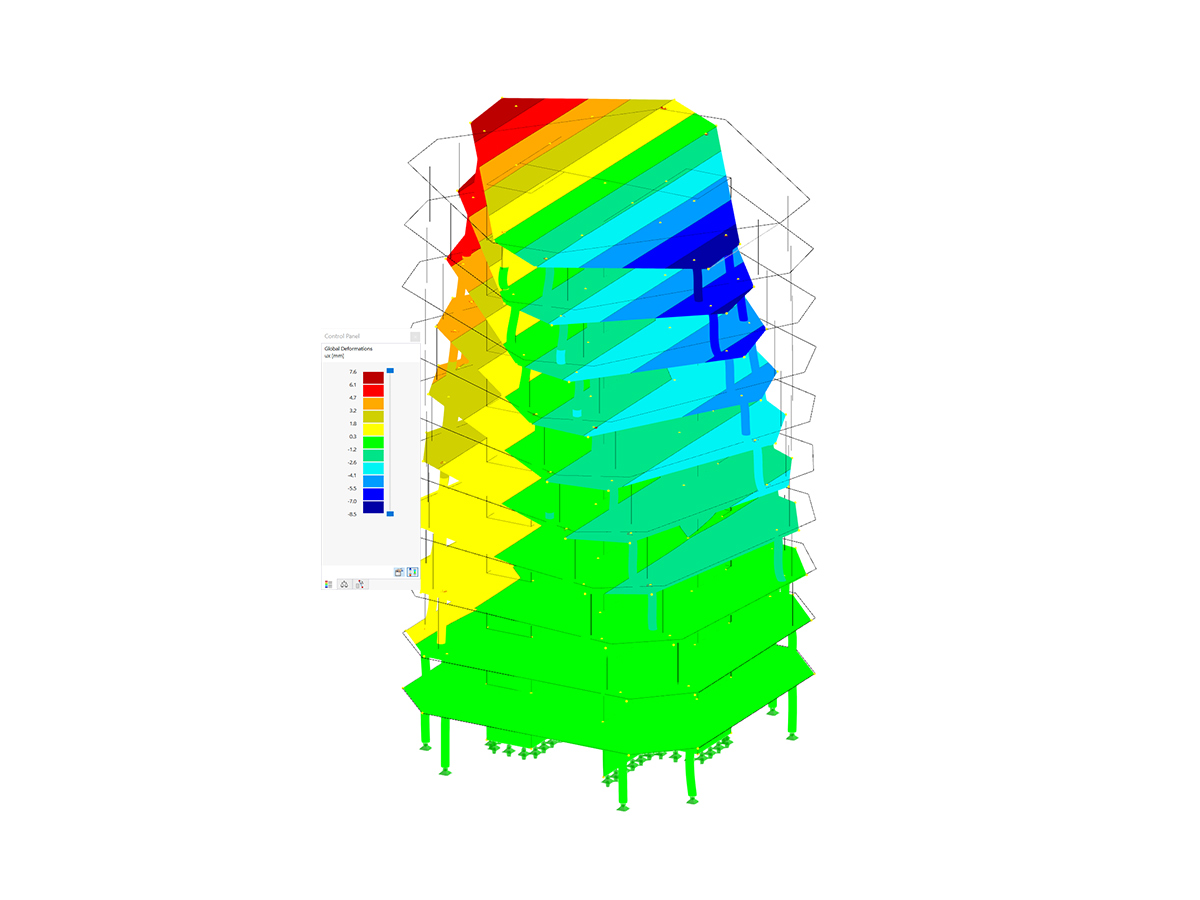
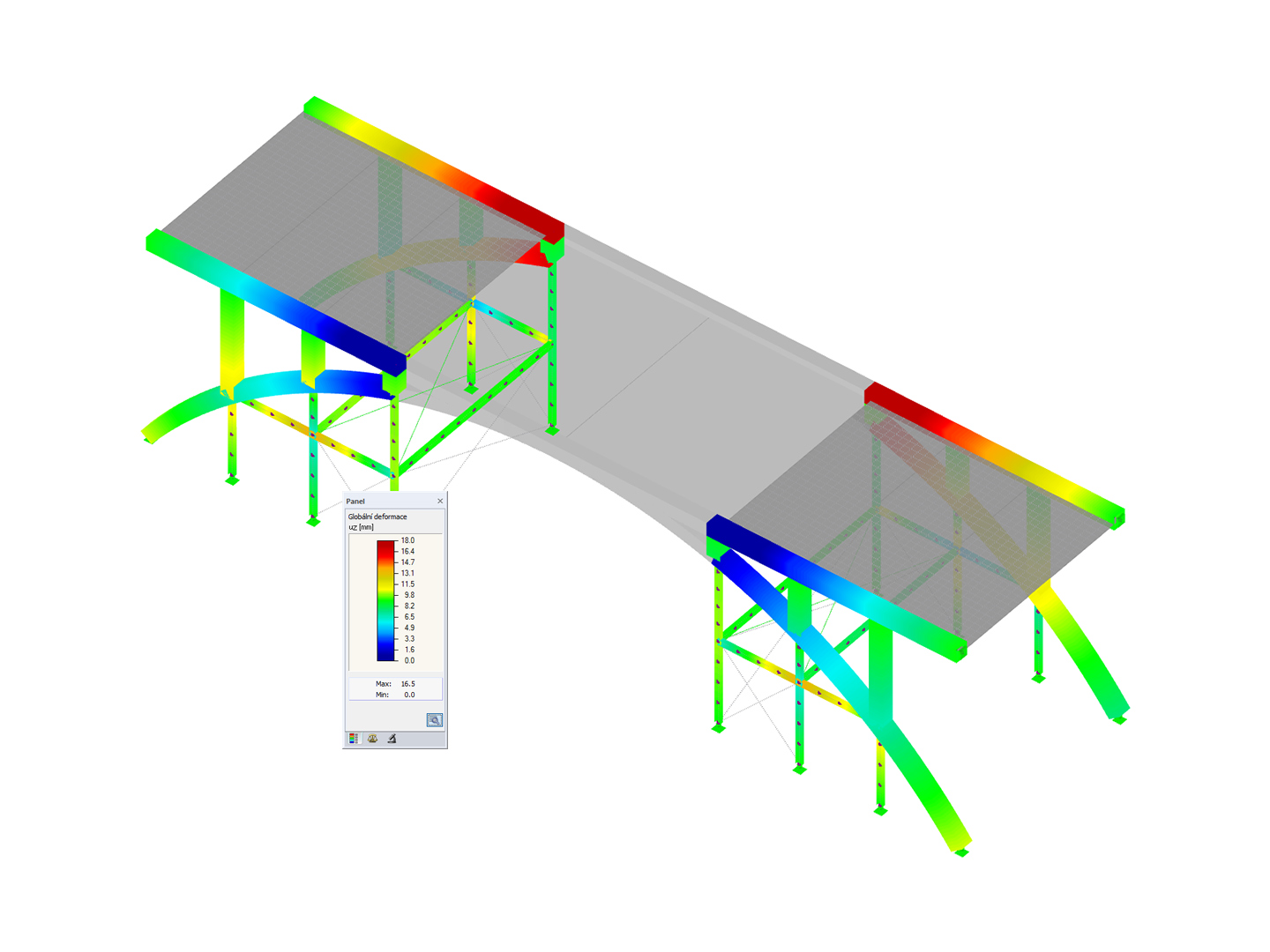


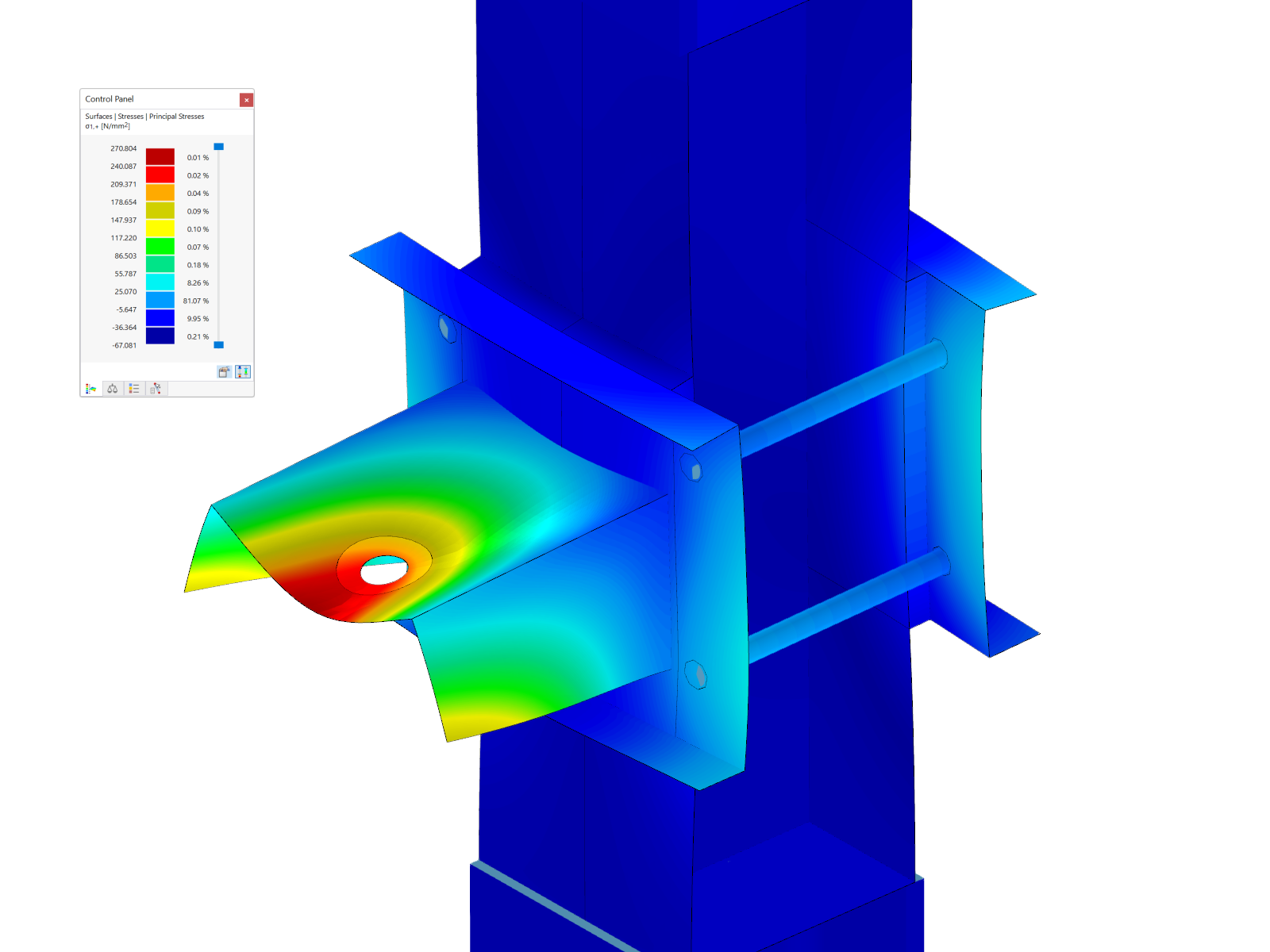
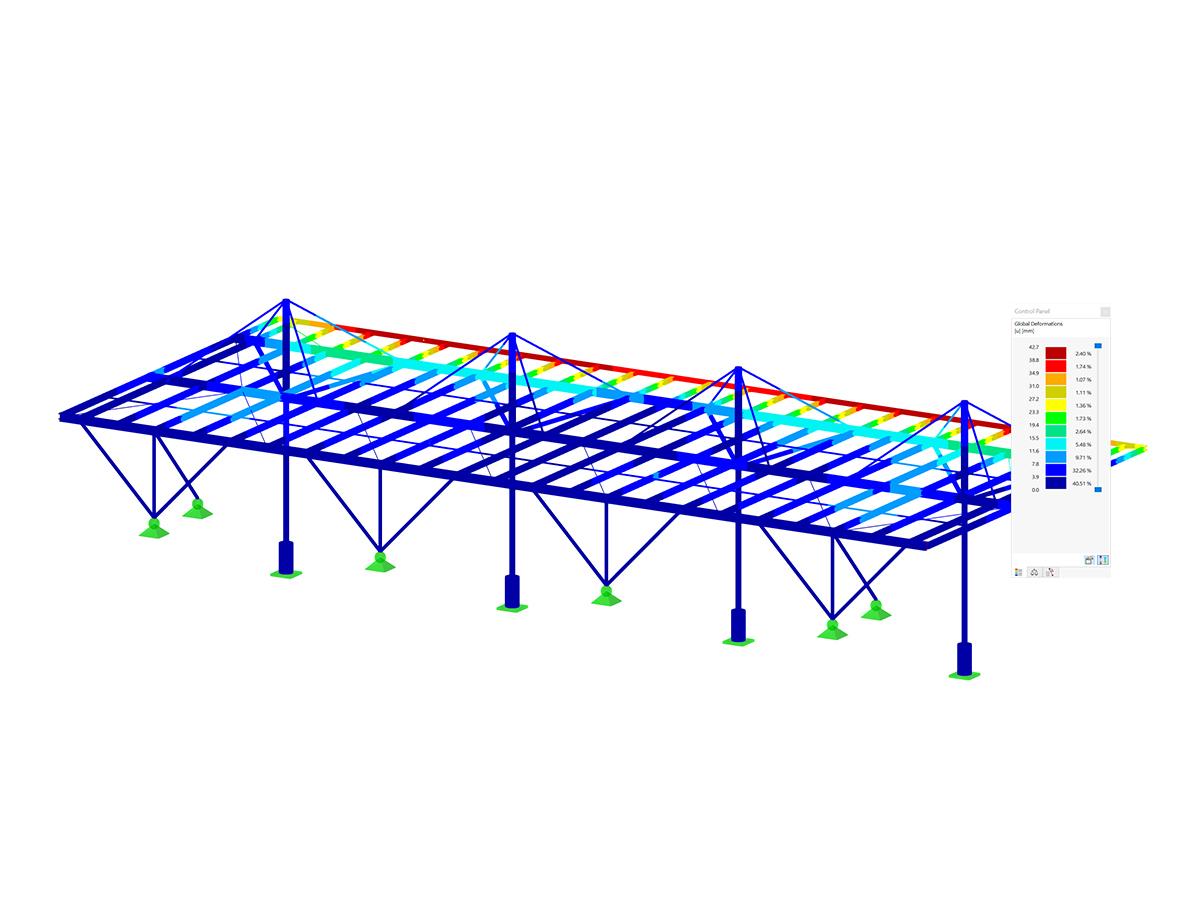
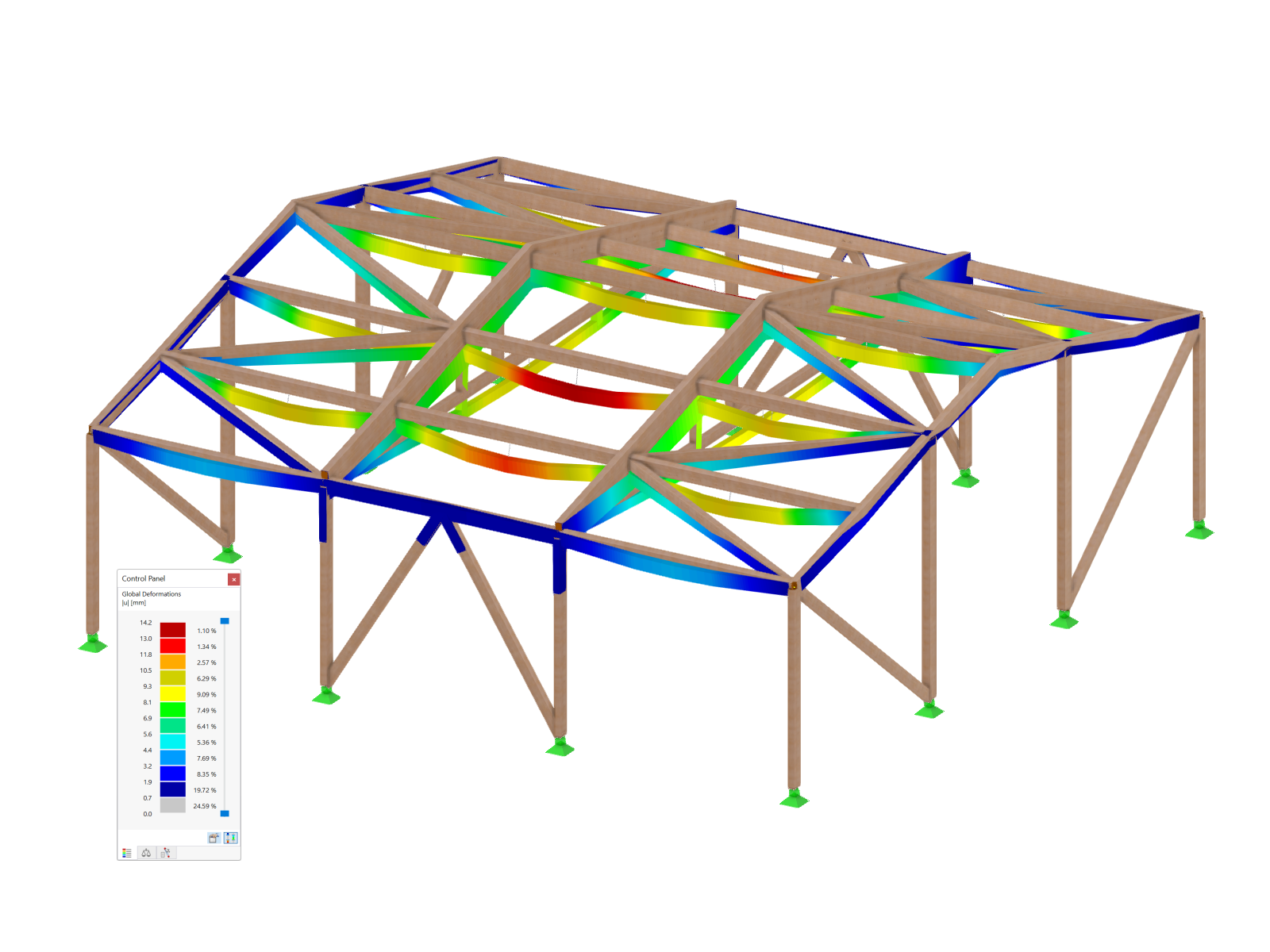
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)