Back to Online Manuals

2375x

000483

Dipl.-Ing. (FH) Robert Vogl

2023-04-27

Select Manual

Overview

Graphical User Interface and Settings

Dlubal Center

Model Base Data

Structure

Imperfections

Load Cases and Combinations

Load Wizards

Loads

Result Objects

Calculation

Results

Guide Objects

Program Functions

Result Evaluation

Printout Reports

Results by Solid

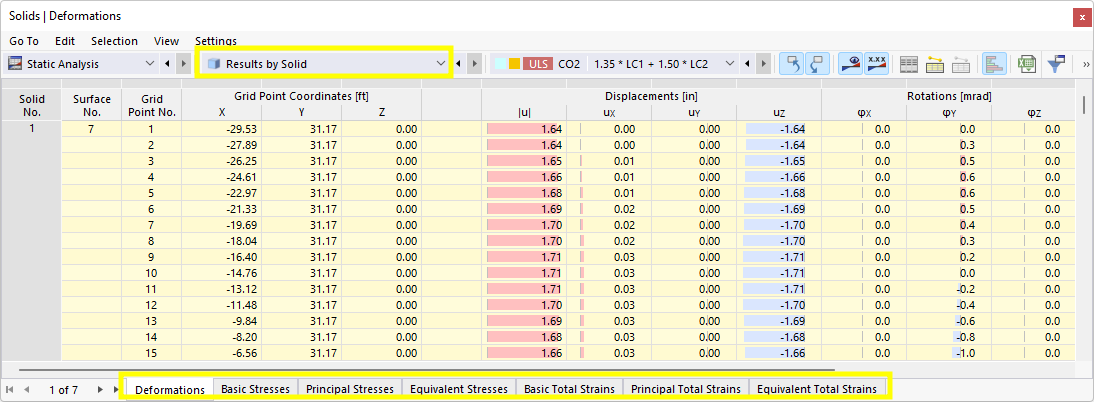
You can display the results for solids graphically using the Solids navigator category. You will find the numerical results of solids in the Results by Solid table category.

Results by Solid in Table

Info

Both the table and the graphic show the results available on the boundary surfaces of the solid. To check the results inside the solid, activate the On FE mesh points option in the Values on Surfaces category in the lower navigator section. You can then read the values in the solid using a clipping plane (see the chapter Clipping Planes).

Deformations

The image Results by Solid in Table shows the table with deformations of the boundary surfaces. Displacements and rotations are displayed in the surface grid points (see the chapter Surfaces ).

Tip

For small surfaces, the grid's standard mesh size of 0.5 m may cause only a few grid points to exist. In this case, adjust the number or distance of grid points to the surface size.

The deformations have the following meaning:

\|u\|	Absolute value of the total displacement
u_X	Displacement in the direction of the global axis X
u_Y	Displacement in the direction of the global axis Y
u_Z	Displacement in the direction of the global axis Z
φ_X	Rotation about the global axis X
φ_Y	Rotation about the global axis Y
φ_Z	Rotation about the global axis Z

Stress

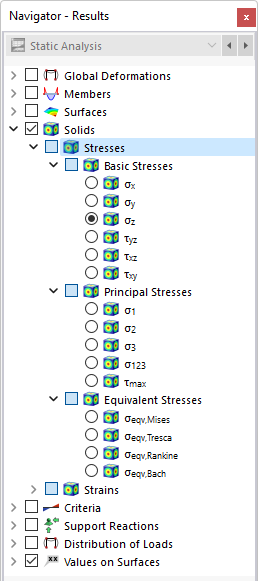
Selecting Solid Stresses in Navigator

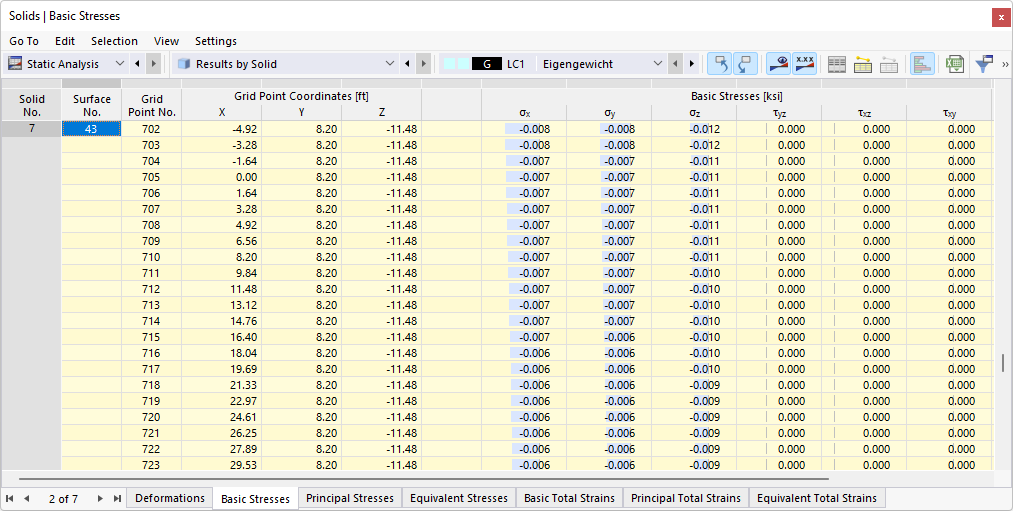
Stresses of Solids in Table

In the navigator, define the stresses to be displayed on the boundary surfaces of solids. The table lists the stresses of these surfaces according to the specifications set in the Result Table Manager .

The solid stresses are divided into the following categories:

Basic Stresses
Principal Stresses
Equivalent Stresses
Stress Invariants

Basic Stresses

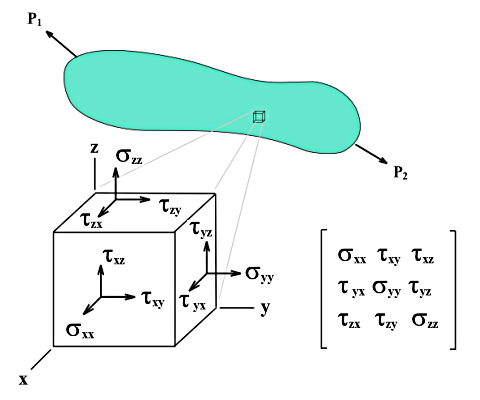
Unlike surface stresses, solid stresses cannot be described by simple equations. The basic stresses σ_x, σ_y, and σ_z as well as the shear stresses τ_yz, τ_xz, and τ_xy are determined directly by the analysis core.

If a cube with the edge lengths d_x, d_y, and d_z is cut from a 3D object with multiaxial loading, the stresses in each cubic surface can be split into normal and shear stresses. Neglecting the spatial force and also the stress differences on parallel surfaces, the stress state can be described by nine stress components in the cube's local coordinate system.

Solid Element with Stress Components

The matrix of the stress tensor is the following:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matrix of Stress Tensor

Principal Stresses

The principal stresses σ₁, σ₂, and σ₃ result from the eigenvalues of the tensor as follows:

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Principal Stresses

The maximum shear stress τ_max is determined according to Mohr's circle:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Maximum Shear Stress

Tip

The σ₁₂₃ navigator entry allows you to graphically display the trajectories of the principal stresses.

Equivalent Stresses

The equivalent stresses σ_v according to von Mises can be determined by two equivalent formulas.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Equivalent Stress σ_v,Mises from Principal Stresses

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Equivalent Stress σ_v,Mises from Basic Stresses

To determine the equivalent stress σ_v according to Tresca , the differences from the principal stresses are examined in order to determine the maximum value.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Equivalent Stress σ_v,Tresca

The equivalent stress σ_v according to Rankine is determined from the greatest absolute values of the principal stresses.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Equivalent Stress σ_v,Rankine

To determine the equivalent stress σ_v according to Bach , the principal stress differences are examined, taking into account Poisson's ratio ν, in order to determine the maximum value.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Equivalent Stress σ_{v, Bach}

Stress Invariants

Stress invariants allow for a coordinate-independent and thus objective description of the stress state of a material. As scalar quantities, they remain unchanged under any rotation of the coordinate system and represent the physically relevant properties of these states independently of the selected tensor representation. Their particular significance lies in the fact that many mechanical phenomena—in particular plastic yielding, failure, and fracture—depend not on individual stress components but on invariant measures. Stress invariants thus form the basis of numerous established flow and failure criteria, such as the von Mises, Tresca, and Drucker-Prager theories.

The mean stress p is linked to the first stress invariant I₁ and describes the hydrostatic stress. It is calculated from the arithmetic mean of the three principal stresses and represents the distance of the stress point from the coordinate origin on the space diagonal.

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Principal stresses
I₁	First stress invariant

Mean Stress p

It characterizes the average axial stress state and is governing in terms of solid changes. Physically, p corresponds to a uniform pressure or tensile state that does not cause any change in shape, but only compression or dilatation. In many materials, especially in soil and rock mechanics as well as in pressure-sensitive materials, p significantly influences the strength and deformation behavior.

The deviatoric stress q is linked to the second invariant of the stress deviator J₂. It is calculated as follows:

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	First stress invariant
I₂	Second stress invariant
J₂	Second deviatoric stress invariant

Deviatoric Stress q

It describes the component of the stress state that is responsible for shape changes (shear distortions) without changing the solid. The deviatoric component drives plastic yielding and failure in ductile materials in particular. The von Mises yield criterion is based directly on J₂ or q and illustrates that plastic deformation is primarily controlled by deviatoric stresses.

The Lode angle θ indicates the location of the stress point in the deviatoric plane. The deviatoric plane is divided into six sectors, so that −30° ≤ θ ≤ 30° applies. The angle is determined as follows:

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Second deviatoric stress invariant: 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)^2 + (σ₃ – σ₂)²]
J₃	Third deviatoric stress invariant: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Lode Angle θ

A pure shear stress results for θ = 0, while for θ = 30°, the stress state σ₁ > σ₂ =& nbsp;σ₃ occurs, which corresponds to a triaxial compression test. From θ = −30°, the stress state of a triaxial tensile test with σ₁ < σ₂ = σ₃ results.

Strains

Selecting Solid Strains in Navigator

Strains on Solids in Table

In the navigator, define the strains to be displayed on the boundary surfaces of solids. The table lists the stresses of these surfaces according to the specifications set in the Result Table Manager .

The solid strains are divided into the following categories:

Basic Total Strains
Principal Total Strains
Equivalent total strains
Strain Invariants

Basic Total Strains

The basic total strains including shear strains are determined directly by the computation kernel. The general definition of the tensor for the spatial strain state is as follows:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tensor for Strain State

The elements of the tensor are defined as follows:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Tensor Elements

Principal Total Strains

The principal total strains ε₁, ε₂, and ε₃ are determined from the basic strains.

Tip

The ε₁₂₃ navigator entry allows you to graphically display the trajectories of the principal total strains.

Equivalent Total Strains

The equivalent total strains ε_v are determined according to four different stress hypotheses as follows.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Comparative Total Strain ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matrix (see below)

Comparative Total Strain ε_v,Tresca (Maximum of Eigenvalue Differences According to Matrix R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Comparative Total Strain ε_v,Rankine (Maximum of Eigenvalues According to Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matrix (see below)

Comparative Total Strain ε_v,Bach (Maximum of Eigenvalue Differences According to Matrix R Taking into Account Poisson's Ratio ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matrix R

Strain Invariants

Strain invariants are properties of the strain tensor that remain independent of the orientation of the coordinate system. They allow for a clear distinction to be made between the change in solid and in shape of a material. This distinction is central to the analysis of material behavior, strength criteria, and plasticity models.

The volumetric strain invariant ε_v corresponds to the isotropic component of the total strains. It is determined from the principal strains:

ε_{v} = ε_{11} + ε_{22} + ε_{33}

Volumetric Strain Invariant, ε_v

The deviatoric strains ε_q or shear strains γ_s describe the pure change in shape without any change in solid. They are calculated as follows:

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

Shear Strain ε_q

Parent Chapter

Results