Zurück zu Online-Handbüchern

1740x

000483

27. April 2023

Handbuch wählen

Übersicht

Benutzeroberfläche und Einstellungen

Dlubal Center

Modell-Basisangaben

Struktur

Imperfektionen

Lastfälle und Kombinationen

Lastassistenten

Lasten

Berechnung

Ergebnisse

Hilfsobjekte

Programmfunktionen

Ergebnisauswertung

Ausdruckprotokolle

Ergebnisse volumenweise

Sie können die Ergebnisse für Volumen grafisch über die Navigator-Kategorie Volumenkörper anzeigen. Die numerischen Volumenergebnisse finden Sie in der Tabellen-Kategorie Ergebnisse volumenweise.

Ergebnisse volumenweise in Tabelle

Info

In der Tabelle und in der Grafik werden die Ergebnisse angezeigt, die an den Begrenzungsflächen des Volumenkörpers vorliegen. Um die Ergebnisse im Inneren des Volumenkörpers zu überprüfen, aktivieren Sie in der unteren Kategorie Werte an Flächen die Option An FE-Netzpunkten. Die Werte im Volumenkörper können Sie dann über eine Clippingebene ablesen (siehe Kapitel Clippingebenen).

Verformungen

Das Bild Ergebnisse volumenweise in Tabelle zeigt die Tabelle mit den Verformungen der Begrenzungsflächen. Die Verschiebungen und Verdrehungen werden in den Flächen-Rasterpunkten ausgegeben (siehe Kapitel Flächen ).

Tipp

Bei kleinen Flächen kann die Standardmaschenweite des Rasters von 0.5 m dazu führen, dass nur wenige Rasterpunkte existieren. Passen Sie in diesem Fall die Anzahl oder den Abstand der Rasterpunkte an die Flächengröße an.

Die Verformungen bedeuten:

\|u\|	Absolutwert der Gesamtverschiebung
u_X	Verschiebung in Richtung der globalen X-Achse
u_Y	Verschiebung in Richtung der globalen Y-Achse
u_Z	Verschiebung in Richtung der globalen Z-Achse
φ_X	Verdrehung um die globale X-Achse
φ_Y	Verdrehung um die globale Y-Achse
φ_Z	Verdrehung um die globale Z-Achse

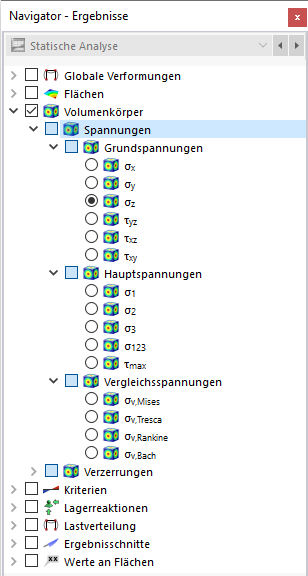
Spannungen

Volumenspannungen im Navigator auswählen

Spannungen der Volumen in Tabelle

Legen Sie im Navigator fest, welche Spannungen an den Begrenzungsflächen der Volumen angezeigt werden sollen. Die Tabelle listet die Spannungen dieser Flächen nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.

Die Volumenspannungen sind in folgende Kategorien unterteilt:

Grundspannungen
Hauptspannungen
Vergleichsspannungen

Volumenspannungen lassen sich nicht wie Flächenspannungen mit einfachen Gleichungen beschreiben. Die Grundspannungen σ_x, σ_y und σ_z einschließlich der Schubspannungen τ_yz, τ_xz und τ_xy werden direkt vom Rechenkern ermittelt.

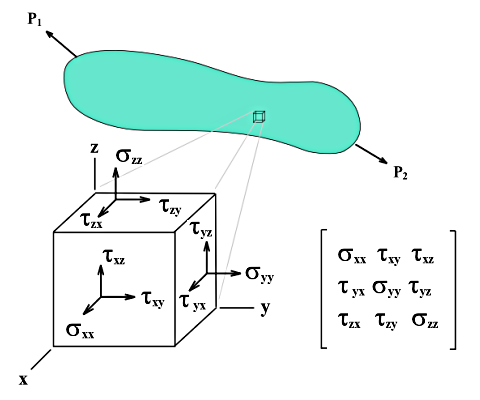
Wird ein Würfel mit den Kantenlängen d_x, d_y und d_z aus einem mehrachsig beanspruchten Körper herausgeschnitten, so können die Spannungen in jeder Würfelfläche in Normal- und Schubspannungen zerlegt werden. Unter Vernachlässigung der Raumkraft und auch der Spannungsunterschiede an parallelen Flächen lässt sich im lokalen Koordinatensystem des Würfels der Spannungszustand durch neun Spannungskomponenten beschreiben.

Volumenelement mit Spannungskomponenten

Die Matrix des Spannungstensors lautet:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matrix des Spannungstensors

Aus den Eigenwerten des Tensors ergeben sich die Hauptspannungen σ₁, σ₂ und σ₃ wie folgt:

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Hauptspannungen

Die maximale Schubspannung τ_max wird nach dem Mohrschen Spannungskreis bestimmt:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Maximale Schubspannung

Tipp

Mit dem Navigatoreintrag σ₁₂₃ können Sie die Trajektorien der Hauptspannungen grafisch darstellen.

Die Vergleichsspannungen σ_v nach von Mises lassen sich durch zwei gleichwertige Formeln bestimmen.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Vergleichsspannung σ_v,Mises aus Hauptspannungen

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Vergleichsspannung σ_v,Mises aus Grundspannungen

Für die Ermittlung der Vergleichsspannung σ_v nach Tresca werden die Differenzen aus den Hauptspannungen untersucht, um daraus den Maximalwert zu bestimmen.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Vergleichsspannung σ_v,Tresca

Die Vergleichsspannung σ_v nach Rankine ermittelt sich aus den größten Absolutwerten der Hauptspannungen.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Vergleichsspannung σ_v,Rankine

Zur Ermittlung der Vergleichsspannung σ_v nach Bach werden die Hauptspannungsdifferenzen unter Berücksichtigung der Querdehnzahl ν untersucht, um daraus den Maximalwert zu bestimmen.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Vergleichsspannung σ_v,Bach

Verzerrungen

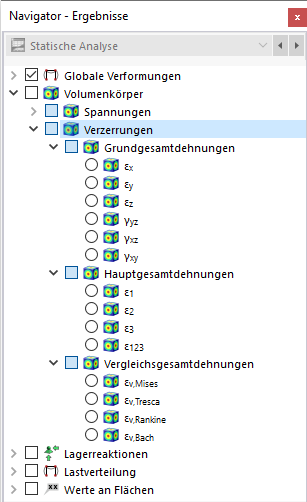
Volumenverzerrungen im Navigator auswählen

Dehnungen der Volumen in Tabelle

Legen Sie im Navigator fest, welche Verzerrungen an den Begrenzungsflächen der Volumen angezeigt werden sollen. Die Tabelle listet die Dehnungen dieser Flächen nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.

Die Volumenverzerrungen sind in folgende Kategorien unterteilt:

Grundgesamtdehnungen
Hauptgesamtdehnungen
Vergleichsgesamtdehnungen

Die Grundgesamtdehnungen einschließlich der Schubverzerrungen werden direkt vom Rechenkern ermittelt. Für den räumlichen Verzerrungszustand lautet die allgemeine Definition des Tensors:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tensor für Verzerrungszustand

Die Elemente des Tensors sind wie folgt definiert:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Tensorelemente

Aus den Grunddehnungen werden die Hauptgesamtdehnungen ε₁, ε₂ und ε₃ ermittelt.

Tipp

Mit dem Navigatoreintrag ε₁₂₃ können Sie die Trajektorien der Hauptdehnungen grafisch darstellen.

Die Vergleichsgesamtdehnungen ε_v werden wie folgt nach vier verschiedenen Spannungshypothesen ermittelt.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Vergleichsgesamtdehnung ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Tresca (Maximum der Eigenwertdifferenzen gemäß Matrix R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Bach (Maximum der Eigenwertdifferenzen gemäß Matrix R unter Berücksichtigung der Querdehnzahl ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matrix R

Übergeordnetes Kapitel

Ergebnisse