Eine Statikanalyse-Einstellung (SA) gibt die Regeln vor, nach denen Lastfälle und Lastkombinationen berechnet werden. Es sind drei Standard-Analysetypen voreingestellt.
Basis
Das Register Basis verwaltet die Einstellungen zur statischen Analyse und elementare Berechnungsparameter.
Analysetyp
Dieser Abschnitt steuert, nach welcher Berechnungstheorie Lastfälle und Lastkombinationen untersucht werden. In der Liste 'Analysetyp' stehen drei Ansätze zur Auswahl.
I. Ordnung
Bei der Berechnung nach Theorie I. Ordnung wird das Gleichgewicht am unverformten System untersucht. Es erfolgt eine lineare Betrachtung, da die Verformungen der Komponenten nicht in die Berechnung einfließen.
Lastfälle werden per Voreinstellung linear nach I. Ordnung berechnet.
II. Ordnung (P-Δ)
Bei der "baustatischen" Theorie II. Ordnung wird das Gleichgewicht am verformten System ermittelt. Die Verformungen werden dabei als klein angenommen. Normalkräfte im System wirken sich auf einen Zuwachs der Biegemomente aus. Die Analyse nach Theorie II. Ordnung kommt somit zum Tragen, wenn die Normalkräfte wesentlich größer sind als die Querkräfte.
Lastkombinationen werden per Voreinstellung nichtlinear nach Theorie II. Ordnung berechnet.
III. Ordnung
Die Theorie III. Ordnung ("Theorie großer Verformungen") berücksichtigt Longitudinal- und Transversalkräfte bei der Berechnung. Nach jedem Iterationsschritt wird die Steifigkeitsmatrix des verformten Systems gebildet. Lasten werden differenziert behandelt: Eine in globale Richtung definierte Last behält ihre Richtung bei, wenn sich die finiten Elemente verdrehen. Wenn die Last in Richtung einer lokalen Stab- oder Flächenachse wirkt, ändert sie ihre Richtung entsprechend der Verdrehung des Elements.
Wenn das Modell Seilstäbe enthält, ist die Berechnung nach III. Ordnung voreingestellt.
Iterative Methode für nichtlineare Analyse
Je nach Analysetyp stehen verschiedene Methoden zur Auswahl, das nichtlineare algebraische Gleichungssystem zu lösen.
Newton-Raphson
Bei Theorie III. Ordnung ist das Verfahren nach Newton-Raphson voreingestellt. Dabei wird das nichtlineare Gleichungssystem numerisch über iterative Näherungen mit Tangenten gelöst. Die tangentiale Steifigkeitsmatrix ermittelt sich als Funktion des aktuellen Verformungszustands; sie wird in jedem Iterationszyklus invertiert. Mit dieser Methode wird in den meisten Fällen eine schnelle (quadratische) Konvergenz erreicht.
Newton-Raphson kombiniert mit Picard
Bei dieser Methode wird zunächst das Verfahren nach Picard verwendet. Nach einigen Iterationen erfolgt ein Wechsel zur Newton-Raphson-Methode. Der Grundgedanke dieses Ansatzes liegt darin, die relativ "unempfindliche" Picard-Methode für die ersten Iterationsschritte zu nutzen, um Instabilitätsmeldungen zu vermeiden. Mit der anfänglichen Näherung wird dann das schnelle Verfahren nach Newton-Raphson genutzt, um den endgültigen Gleichgewichtszustand zu finden.
Picard
Die Methode nach Picard – auch Sekantenverfahren genannt – kann als finite Differenzennäherung der Newton-Raphson-Methode verstanden werden. Es wird die Differenz zwischen dem aktuellen und dem ursprünglichen Iterationslauf im aktuellen Laststeigerungsschritt betrachtet. Diese Methode konvergiert meist langsamer als das Berechnungsverfahren nach Newton-Raphson. Sie erweist sich jedoch auch unempfindlicher gegenüber nichtlinearen Problemen, wodurch die Berechnung stabiler abläuft.
Newton-Raphson mit Durchschlagproblem
Diese Methode eignet sich zur Lösung von Durchschlagproblemen, bei denen ein Bereich mit Instabilität überwunden werden muss. Wenn eine Instabilität vorliegt und die Steifigkeitsmatrix nicht invertiert werden kann, wird die Steifigkeitsmatrix des letzten stabilen Iterationsschritts verwendet. Es wird mit dieser Matrix weitergerechnet, bis wieder der Stabilitätsbereich erreicht ist.
Dynamische Relaxation
Die letzte Methode eignet sich für Berechnungen nach Theorie III. Ordnung und zur Lösung von Durchschlagproblemen. Bei diesem Ansatz wird ein künstlicher Zeitparameter eingeführt. Unter Berücksichtigung von Trägheit und Dämpfung lässt sich die Aufgabe dann als dynamisches Problem behandeln. Dieser Ansatz benutzt die explizite Zeit-Integrationsmethode; die Steifigkeitsmatrix wird dabei nicht invertiert. Für eine Berechnung mit dynamischer Relaxation darf kein Teil des Modells ein spezifisches Gewicht von null aufweisen.
Diese Methode schließt auch die Rayleigh-Dämpfung ein, die über die Konstanten α und β nach folgender Gleichung mit den Ableitungen nach der Zeit definiert werden kann:
|
M |
konzentrierte (diagonale) Massenmatrix |
|
C |
diagonale Dämpfungsmatrix C = αM + βdiag[K11(u),K22(u),...,Knn(u)] |
|
K |
Steifigkeitsmatrix |
|
f |
Vektor der äußeren Kräfte |
|
u |
Diskretisierter Verschiebevektor |
Steuerelemente für nichtlineare Analyse
Die 'Maximale Anzahl der Iterationen' legt fest, wie viele Rechendurchläufe bei einer Analyse nach Theorie II. oder III. Ordnung sowie bei nichtlinear wirkenden Objekten höchstens erfolgen. Erreicht die Berechnung dieses Limit, ohne dass sich ein Gleichgewicht einstellt, erscheint eine entsprechende Meldung. Sie können dann entscheiden, ob die Ergebnisse angezeigt werden sollen.
Die 'Anzahl der Laststufen' ist für Analysen nach Theorie II. oder III. Ordnung relevant. Bei der Berücksichtigung der großen Verformungen ist es oft schwierig, ein Gleichgewicht zu finden. Instabilitäten können umgangen werden, indem die Belastung in mehreren Schritten aufgebracht wird. Wenn Sie beispielsweise zwei Laststufen vorgeben, wird im ersten Schritt die Hälfte der Last angesetzt. Es wird so lange iteriert, bis das Gleichgewicht gefunden ist. Im zweiten Schritt wird dann die volle Belastung auf das bereits verformte System aufgebracht und wieder bis zum Gleichgewicht iteriert.
Optionen I
In diesem Abschnitt können Sie verschiedene 'Sondereinstellungen aktivieren', um die Berechnung nach Theorie II. oder III. Ordnung zu beeinflussen.
Einstellungen für Standardgenauigkeit und -toleranz ändern
Wenn Sie das Kontrollfeld 'Einstellungen für Standardgenauigkeit und -toleranz ändern' anhaken, wird im Dialog das Register Genauigkeit und Toleranz ergänzt. Dort können Sie die Konvergenzkriterien anpassen.
Alle Nichtlinearitäten ignorieren
Mit dem Kontrollfeld 'Alle Nichtlinearitäten ignorieren' können Sie die nichtlinearen Eigenschaften von Elementen für die Berechnung deaktivieren. Zugstäbe beispielsweise verbleiben dann im Modell, sobald Druckkräfte auftreten. Die nichtlinearen Eigenschaften sollten Sie jedoch nur zu Testzwecken unterdrücken, beispielsweise um die Ursache einer Instabilität zu finden. Manchmal sind fehlerhaft definierte Ausfallkriterien verantwortlich für den Abbruch der Berechnung.
Optionen II
Belastung mittels Multiplikationsfaktor modifizieren
Nach dem Anhaken des Kontrollfeldes können Sie einen Faktor k festlegen, mit dem alle Lasten multipliziert werden sollen.
In älteren Normen besteht die Forderung, Belastungen global mit einem Faktor zu multiplizieren, um die Effekte nach Theorie II. Ordnung für Stabilitätsnachweise zu vergrößern. Die Bemessung wiederum hat mit den Gebrauchslasten zu erfolgen. Beide Forderungen können erfüllt werden, indem ein Faktor größer 1 eingegeben und das Kontrollfeld 'Ergebnisse durch Lastfaktor zurückdividieren' aktiviert wird.
Für Untersuchungen nach aktuellen Normen sollte die Belastung nicht mittels Faktoren bearbeitet werden. Stattdessen sind die Teilsicherheits- und Kombinationsbeiwerte bei der Überlagerung in den Bemessungssituationen zu berücksichtigen.
Entlastende Wirkung durch Zugkräfte in Stäben berücksichtigen
Zugkräfte haben auf ein vorverformtes System eine entlastende Wirkung. Dadurch wird die Verformung verringert und das System stabilisiert. Dieser Effekt wird im Regelfall bei der Berechnung nach II. Ordnung und III. Ordnung ausgenutzt, beispielsweise bei Hallen mit Verbänden oder biegebeanspruchten Tragwerken allgemeiner Art. Bei unterspannten Trägern kann die Zugkraftentlastung unter Umständen aber zu einer unerwünschten Verringerung der Verformungen und Schnittgrößen führen.
Überprüfung der Stabilität anhand der Verformungsrate
Wenn Sie das Kontrollfeld anhaken, überprüft RFEM bei der Berechnung, wie sich die Verformungen im Laufe der Iterationen entwickeln. Wenn die Verschiebungen oder Verdrehungen stark ansteigen und ein programminternes Limit überschreiten, bricht die Berechnung mit einer Instabilitätsmeldung ab.
Versuchen, instabile Struktur zu berechnen
Über dieses Kontrollfeld kann versucht werden, ein instabiles Modell berechenbar zu machen: RFEM setzt beim ersten Rechenschritt kleine Federn an, die das Modell für die erste Iteration stabilisieren. Nach dem Erreichen eines stabilen Anfangszustandes werden diese Federn für die folgenden Iterationen wieder entfernt.
Verschiebungen durch Stablast des Typs 'Rohrinnendruck'
Das Kontrollfeld ist für die Stablast Rohrinnendruck relevant. Der so genannte Bourdon-Effekt beschreibt das Bestreben eines gebogenen Rohres, sich unter dem Einfluss von Druck gerade zu biegen. Die Umfangsspannungen und Axialspannungen aus der Innendrucklast führen – unter Berücksichtigung der Materialsteifigkeit und Querdehnung – zu einer axialen Längsdehnung des Rohres.
Ein Fachbeitrag beschreibt in einem Beispiel, wie der Innendruck von Rohren berechnet wird.
Ergebnisse aller Laststufen speichern
Wenn die Belastung stufenweise aufgebracht wird (siehe Abschnitt Steuerelemente für nichtlineare Analyse), können Sie mit dem Kontrollfeld die Ausgabe der Zwischenergebnisse erzwingen, um die Ergebnisse der einzelnen Laststufen zu überprüfen.
Unsymmetrischer direkter Gleichungslöser
Bei einem nichtlinearen Materialmodell (siehe Kapitel Nichtlineares Materialverhalten) mit unsymmetrischen Eigenschaften für Zug und Druck wird ein unsymmetrischer direkter Gleichungslöser benutzt. Das Kontrollfeld bietet die Möglichkeit, diesen Gleichungslöser auch für andere Materialmodelle zu verwenden, wie beispielsweise für das Materialmodell Isotrop nichtlinear elastisch.
Gleichgewicht für unverformte Struktur
Das Kontrollfeld ermöglicht es, eine sich nicht verformende Struktur zu analysieren – also ein System, dessen Verformungen null bleiben. Diese Analyseoption kann nützlich sein, wenn ein System beispielsweise infolge eines Lastfalls unter Spannung steht, während die daraus folgenden Verformungen als abgeklungen angesehen werden können.
Ein Anwendungsgebiet für die Berechnung des Gleichgewichts für die unverformte Struktur stellt der Primärspannungszustand der geotechnischen Analyse dar. Dabei sollen im Rahmen eines Lastfalls oder einer Lastkombination die aus der Vorbelastung des Bodens wirkenden Spannungen ermittelt werden. Die Verformungen dieses Lastfalls oder dieser Kombination jedoch sind nicht von Interesse und damit nicht Gegenstand einer weiteren Verwendung.
Basiseinstellungen
Das Register Basiseinstellungen verwaltet grundlegende Vorgaben für die Berechnung.
Dauerlastverhältnis
Das Kontrollfeld 'Für Lastkombinationen ermitteln' bietet die Möglichkeit, den Anteil einer permanent wirkenden Last in einer Lastkombination zu bestimmen. Wählen Sie die Lastkombination in der Liste aus oder legen mit der Schaltfläche
![]() eine neue Lastkombination an. In der Liste 'Ergebniswert vergleichen' können Sie dann festlegen, welche Anteile statisch oder variabel wirken.
eine neue Lastkombination an. In der Liste 'Ergebniswert vergleichen' können Sie dann festlegen, welche Anteile statisch oder variabel wirken.
Der Anteil der Dauerlast kann bei der Bemessung normgerecht berücksichtigt werden.
Methode für Gleichungssystem
Die Auswahlfelder steuern, welche Methode zum Lösen des Gleichungssystems benutzt wird. Um Missverständnissen vorzubeugen: Auch bei der direkten Lösung des Gleichungssystems erfolgt eine iterative Berechnung, wenn Nichtlinearitäten vorliegen oder nach Theorie II. und III. Ordnung gerechnet wird. 'Direkt' und 'Iterativ' beziehen sich auf die Datenverwaltung während der Berechnung.
Welche Gleichungslösermethode schneller zu Ergebnissen führt, hängt von der Komplexität des Modells sowie von der Größe des verfügbaren Hauptspeichers (RAM) ab. Bei kleinen und mittelgroßen Systemen ist die direkte Methode effektiver.
Bei sehr großen Systemen führt die iterative Methode schneller zu Ergebnissen.
Platten-Biegetheorie
Flächen können nach den Biegetheorien von 'Mindlin' oder 'Kirchhoff' berechnet werden. Bei der Berechnung nach Mindlin werden Querkraftverformungen eingeschlossen, nach Kirchhoff werden diese nicht berücksichtigt. Die Berechnungsoption Mindlin eignet sich deshalb für die relativ dicken Platten und Schalen des Massivbaus; die Option Kirchhoff ist für relativ dünne Flächen wie beispielsweise Stahlbleche zu empfehlen.
Einstellungen für iterative Methode
Die Kontrollfelder dieses Abschnitts sind für den Analysetyp 'II. Ordnung (P-Δ)' von Bedeutung.
Schnittgrößen auf verformte Struktur beziehen
Die Schnittgrößen von Stäben werden in der Regel auf die veränderte Lage der Stabkoordinatensysteme bezogen ausgegeben, die im verformten System vorliegt. Soll die Ausgabe auf das unverformte Ausgangssystem bezogen erfolgen, können Sie die relevanten Stabschnittgrößen durch Deaktivieren der entsprechenden Kontrollfelder festlegen.
Prozentualer Anteil der Iterationen nach Newton-Raphson kombiniert mit Picard
Die Lösungsmethode nach Picard geht von Sekantensteifigkeiten aus, die Methode nach Newton-Raphson von Tangentensteifigkeiten. Bei der Berechnungsoption Newton-Raphson kombiniert mit Picard werden in den ersten Iterationen Sekantensteifigkeiten benutzt, ehe Tangentensteifigkeiten für die restlichen Iterationen angesetzt werden. Der Anteil der ersten Iterationen mit Sekantensteifigkeiten ist auf die Gesamtanzahl der Iterationen bezogen.
Massenumwandlung in Last
Lasten können nicht nur als Kräfte und Momente, sondern auch in Form von Massen definiert werden. In der statischen Berechnung jedoch haben Massen keine Wirkung. Sollen sie berücksichtigt werden, so aktivieren Sie das Kontrollfeld 'Aktive Masse'. Geben Sie dann den 'Faktor in Richtung' an, um die Wirkung der Masse zu beschreiben. Die Massen werden so vor der Berechnung in Kräfte umgewandelt und fließen in die Ermittlung der Schnittgrößen ein.
Mit der Schaltfläche
![]() können Sie zwischen der Eingabe des Massenfaktors und der Direktangabe der Beschleunigung wechseln. Die Beschriftung der Eingabefelder wird entsprechend angepasst.
können Sie zwischen der Eingabe des Massenfaktors und der Direktangabe der Beschleunigung wechseln. Die Beschriftung der Eingabefelder wird entsprechend angepasst.
Reaktivierung
Das Register Reaktivierung ist verfügbar, sobald ein Stab mit nichtlinearen Eigenschaften im Modell existiert. Hier können Sie steuern, wie ausfallende Stäbe bei der Berechnung behandelt werden.
Ausfallende Stäbe sind oft die Ursache von Instabilitätsproblemen, beispielsweise wenn ein Stabmodell durch Zugstäbe ausgesteift ist. Wegen der Stielverkürzungen infolge der Vertikallast erhalten die Zugstäbe im ersten Berechnungsdurchgang kleine Druckkräfte. Sie werden aus dem System entfernt. Im zweiten Durchgang wird das Modell ohne diese Zugstäbe instabil. Mit den Möglichkeiten des Abschnitts 'Reaktivierung der ausfallenden Stäbe' können Sie versuchen, eine Berechnung ohne Fehlermeldung zu erreichen.
Verformung der ausfallenden Stäbe überprüfen und diese ggf. reaktivieren
RFEM untersucht in jeder Iteration die Knotenverschiebungen. Sollten sich beispielsweise die Stabenden eines ausgefallenen Zugstabes voneinander entfernen, wird der Stab wieder in der Steifigkeitsmatrix verwendet.
In manchen Fällen kann das Reaktivieren von Stäben problematisch sein: Ein Stab wird nach der ersten Iteration entfernt, nach der zweiten Iteration wieder eingeführt, nach der dritten wieder entfernt, etc. Die Berechnung würde diese Schlaufe bis zum Erreichen der maximal möglichen Iterationen durchlaufen, ohne zu konvergieren. Die 'Maximale Anzahl der Reaktivierungen' verhindert diesen Effekt. Hier können Sie festlegen, wie oft ein Stabelement wieder eingeführt werden darf, ehe es endgültig aus der Steifigkeitsmatrix genommen wird.
Besondere Behandlung
Wenn Sie das Kontrollfeld 'Besondere Behandlung' anhaken, stehen zwei Methoden zum Umgang mit ausfallenden Stäben zur Auswahl. Sie sind mit der oben beschriebenen Reaktivierung kombinierbar.
- Ausfallende Stäbe einzeln in den Iterationen nacheinander entfernen
Nach der ersten Iteration werden beispielsweise nicht alle Zugstäbe mit einer Druckkraft auf einmal entfernt, sondern nur der Zugstab mit der größten Druckkraft. In der zweiten Iteration fehlt dann nur ein Stab in der Steifigkeitsmatrix. Anschließend wird wieder der Zugstab mit der größten Druckkraft entfernt. Auf diese Weise zeigt das System oft wegen der Umlagerungseffekte ein besseres Konvergenzverhalten.
Diese Berechnungsvariante benötigt mehr Zeit, da eine größere Anzahl an Iterationen durchlaufen werden muss. Zudem ist sicherzustellen, dass im Register 'Basis' eine ausreichende Maximale Anzahl der Iterationen vorgesehen ist.
- Ausfallenden Stäben sehr kleine Steifigkeit zuweisen
Die ausgefallenen Stäbe werden nicht aus der Steifigkeitsmatrix entfernt, sondern es wird ihnen eine sehr kleine Steifigkeit zugewiesen. Diese können Sie im Eingabefeld 'Abminderungsbeiwert der Steifigkeit' festlegen: Der Faktor 1000 bedeutet, dass die Stabsteifigkeit auf 1/1000 reduziert wird.
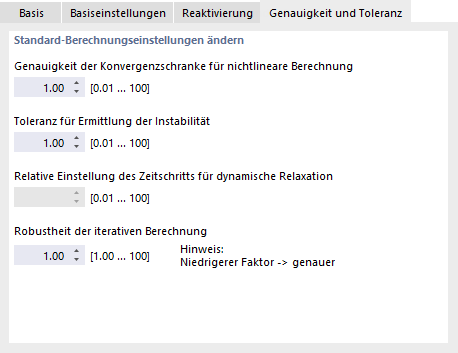
Genauigkeit und Toleranz
Das Register Genauigkeit und Toleranz bietet die Möglichkeit, Einfluss auf die Konvergenz- und Toleranzparameter der Berechnung zu nehmen. Sie sollten die Voreinstellungen jedoch nur in Ausnahmefällen ändern.
Genauigkeit der Konvergenzschranke für nichtlineare Berechnung
Wenn nichtlineare Effekte wirken oder die Analyse nach Theorie II. oder III. Ordnung erfolgt, kann die Berechnung über die Konvergenzschranke beeinflusst werden.
Die Normalkraftänderung der letzten beiden Iterationen wird stabweise verglichen. Sobald diese Änderung einen bestimmten Bruchteil der maximalen Normalkraft erreicht hat, endet die Berechnung. Während der Iterationen kann aber der Fall eintreten, dass die Normalkräfte zwischen zwei Werten oszillieren. Diesen Pendeleffekt können Sie unterbinden, indem Sie die "Empfindlichkeit" anpassen.
Die Genauigkeit beeinflusst auch das Konvergenzkriterium für Verformungsänderungen bei der Berechnung nach Theorie III. Ordnung, bei der geometrische Nichtlinearitäten berücksichtigt werden. Voreingestellt ist der Faktor 1.00. Der minimale Faktor ist 0.01, der Maximalwert beträgt 100.00. Je kleiner der Wert, desto näher muss der Konvergenzterm am Vergleichsterm liegen. Die Ergebnisgenauigkeit wird entsprechend erhöht.
Toleranz für Ermittlung der Instabilität
Es gibt verschiedene Ansätze, um das Stabilitätsverhalten eines Modells zu untersuchen. Keiner kann jedoch mit absoluter Verlässlichkeit singuläre Steifigkeitsmatrizen aufdecken.
RFEM benutzt zwei Vorgehensweisen zur Ermittlung der Instabilität: Zum einen werden die Elemente auf der Hauptdiagonale der Steifigkeitsmatrix absolut immer mit der gleichen Nummer in den Iterationen verglichen. Zum anderen wird jedes Element der Hauptdiagonale relativ zur benachbarten Nummer untersucht. Die Toleranz kann im Eingabefeld angepasst werden. Je kleiner der Toleranzwert, desto näher wird die die Instabilitätsschranke eines Modells näher an die exakte Instabilitätsstelle geschoben. Die Ergebnisgenauigkeit wird entsprechend erhöht.
Relative Einstellung des Zeitschritts für dynamische Relaxation
Der Zeitparameter steuert die Berechnung nach der Methode der dynamischen Relaxation. Je kleiner Wert, desto kleiner ist der Zeitschritt, mit dem sämtliche Antwortschwankungen erfasst werden. Die Genauigkeit der Ergebnisse wird entsprechend erhöht.
Robustheit der iterativen Berechnung
Bei Konvergenzproblemen mit der Newton-Raphson-Methode kann die Robustheit gefestigt werden, um das "Überspringen" der Lösung zu unterbinden. Mit einer Verkleinerung des Werts wird die Anzahl der möglichen Lösungen beim Vorhandensein eines nicht konvergierenden horizontalen Lösungsasts und somit die Möglichkeit auf ein gültiges Ergebnis innerhalb der vorgegebenen Iterationen reduziert. Dabei kann es erforderlich sein, die Anzahl der maximalen Iterationen zu erhöhen.