1D-Elemente
Für Stabelemente wird angenommen, dass der Querschnitt bei der Verformung eben bleibt. Zur Abbildung von Balken, Fachwerkstäben, Rippen, Seilen und starren Kopplungen werden 1D-Elemente benutzt. Ein 1D-Stabelement hat insgesamt zwölf Freiheitsgrade − sechs am Anfang und sechs am Ende des Elements, jeweils für die Verschiebungen (ux, uy, uz) und Verdrehungen (φx, φy, φz). Zug, Druck und Torsion werden bei der linearen Berechnung als lineare Funktionen der Stabachse x ausgedrückt, unabhängig von Biegung und Querkraft. Diese werden durch ein Polynom dritter Ordnung in x angenähert, einschließlich des Einflusses der Schubbeanspruchungen aus den Querkräften Vy und Vz. Die Steifigkeitsmatrix KL(12, 12) beschreibt das lineare Verhalten der 1D-Elemente. Die gegenseitige Interaktion zwischen Normalkraft und Biegung bei geometrisch nichtlinearen Problemen wird in der Steifigkeitsmatrix KNL(12, 12) ausgedrückt. Weitere Informationen finden Sie in [1] und [2].
Für die Berechnung nach Theorie III. Ordnung empfiehlt sich eine Netzverdichtung der Linien, damit die Stabergebnisse mit der entsprechenden Genauigkeit ermittelt werden können.
2D-Elemente
Bei Flächen werden 2D-Elemente erzeugt. Wo keine Viereckselemente verwendet werden können, fügt der Netzgenerierer Dreieckselemente ein.
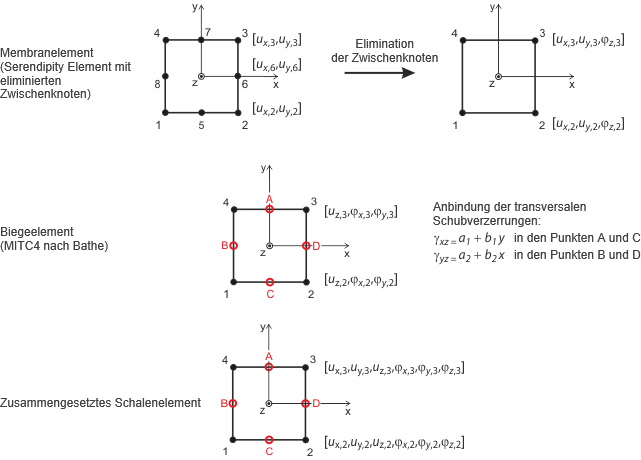
Die Freiheitsgrade der Vierecks- und Dreieckselemente sind in den Knotenpunkten die gleichen wie bei 1D-Elementen: Verschiebungsfreiheitsgrade (ux, uy, uz) und Verdrehungsfreiheitsgrade (φx, φy, φz). So ist die Verträglichkeit zwischen 1D- und 2D-Elementen in den Knoten gewährleistet. Die Parameter sind im ebenen lokalen Element-Koordinatensystem definiert und werden beim Zusammenstellen der globalen Steifigkeitsmatrix in das globale Koordinatensystem umgerechnet.
Das Bild Viereckselemente für Schalen zeigt den Ansatz für ebene Schalenelemente. Er basiert auf der Theorie von Mindlin/Reissner. Um die direkte Kopplung mit Stabelementen zu gewährleisten, wird ein quadratischer Ansatz in der Schalenebene gewählt (ux, uy). Über eine Elimination der Zwischenknoten entsteht ein Vierknoten-Element mit zusätzlichen Verdrehfreiheitsgraden in x-, y- und z-Richtung. So ist bei Scheibenelementen eine direkte Kopplung mit Balkenelementen möglich. Basierend auf einer gemischten Interpolation der transversalen Verschiebungen, Querschnittsdrehungen und transversalen Schubverzerrungen werden die von Bathe und Dvorkin [3] vorgestellten MITC-Elemente (Mixed Interpolation of Tensorial Components) verwendet: MITC3+ für Dreiecke, MITC4 für Vierecke.
Derzeit erfolgt die Berücksichtigung von Stabelementen durch eine direkte Lösung der Differenzialgleichung nach Theorie II. Ordnung. Die Berücksichtigung von Verdrillungseffekten ist unter Verwendung der Saint-Venantschen Torsion nicht möglich.
Die Membranberechnung basiert auf den Prinzipien von Bergan [4] [5] [6]. Die Grundfunktionen werden beispielsweise bei Dreieckselementen in drei Starre-Körper-Verformungen, drei konstante Dehnungszustände und drei spezielle lineare Verläufe von Spannungen und Dehnungen unterteilt. Das Verformungsfeld im Element ist quadratisch und das Spannungsfeld linear. Die Elementsteifigkeitsmatrix KL wird anschließend in neun gemeinsame Parameter der Typen ux, uy, φz umgewandelt. Die Komponenten dieser Matrix werden gemeinsam mit den Komponenten für Biegung und Schub in die Gesamtsteifigkeitsmatrix eingefügt (18, 18). Diese Matrix ist das Ergebnis des Lynn/Dhillon-Konzepts. Dabei werden so genannte Mindlin-Platten angesetzt (Platten, bei denen die Schubverzerrung eine Rolle spielt) und nach Timoshenko berechnet. RFEM findet so die korrekte Lösung sowohl für dicke als auch für dünne Platten (Navier-Platten).
Bei geometrisch nichtlinearen Problemen ist die oben erläuterte Zerlegung des Spannungs-Dehnungszustands in einen ebenen Zustand und in Biegung/Schub nicht möglich. In der Matrix KNL ist die gegenseitige Beeinflussung dieser Zustände berücksichtigt. RFEM verwendet eine relativ einfache, aber effektive Form der Matrix KNL, die auf den Ansätzen von Zienkiewicz [7] basiert. Es wird die quadratische Komponente ε2 des Green/Lagrange-Dehnungstensors ε = ε1 + ε2 herangezogen. Dabei werden ein linearer Verlauf von uz(x, y) des ebenen Spannungszustandes und lineare Verläufe von ux(x, y) und uy(x, y) bei der Wechselwirkung mit Biegung vorausgesetzt. Diese Annahme ist möglich, da die Hauptinteraktionswirkung von der ersten Ableitung der Differenzialgleichung abhängig ist und der Einfluss der Komponenten höherer Ordnung sehr schnell mit der Teilung in kleinere Elemente abnimmt. Numerische Untersuchungen belegen die Richtigkeit dieses Verfahrens.
3D-Elemente
Bei einem Volumenkörper werden 3D-Elemente verwendet. Folgende Elementtypen sind in RFEM implementiert: Tetraeder, Pentaeder (Prisma, Pyramide) und Hexaeder. Auf eine ausführliche Darstellung der verwendeten Elemente und Matrizen wird hier verzichtet. Genaue Informationen sind in Sevcik, 3D Finite Elements with Rotational Degrees of Freedom [8] zu finden. Diese Dokumentation können Sie bei Dlubal Software anfordern.
Generell sind bei Volumen alle Drehfreiheitsgrade kritisch einzustufen. Da die Verformung eines Volumens ausschließlich aus den Verschiebungsvektoren bestimmt wird, wirkt sich die Verdrehung eines Netzknotens (beispielsweise infolge singulär eingeleiteter Torsion) nicht auf die Verformung im Volumenkörper aus.