Éléments finis dans RFEM

Éléments 1D

Pour les éléments de barre, il est supposé que la section reste plane lors de la déformation. Les « éléments 1D » sont utilisés pour représenter les poutres, les treillis, les nervures, les câbles et les couplages rigides. Un élément de barre 1D a un total de douze degrés de liberté - six au début et six à la fin de l'élément, chacun pour les déplacements (u_x, u_y, u_z) et les rotations (φ_x, φ_y, φ_z). Lors du calcul linéaire, la traction, la compression et la torsion sont exprimées comme des fonctions linéaire de l'axe de barre x et indépendantes de la flexion et cisaillement. Ces fonctions sont approximées par un polynôme du troisième ordre en x, y compris l'influence des contraintes de cisaillement des efforts tranchants V_y et V_z. La matrice de rigidité K_L (12, 12) décrit le comportement linéaire des éléments 1D. L'interaction mutuelle de l'effort normal et de la flexion en cas de problèmes géométriquement non-linéaires est exprimée dans la matrice de rigidité K_NL (12, 12). Pour en savoir plus, voir [1] et [2].

Pour les calculs selon l'analyse des grandes déformations, il est recommandé d'utiliser un raffinement de maillage linéique afin que les résultats de barre puissent être déterminés avec la précision correspondante.

Éléments 2D

Pour les surfaces, des éléments 2D sont créés. Lorsque des éléments quadrangulaires ne peuvent pas être utilisés, le générateur de maillage insère des éléments triangulaires.

Les degrés de liberté des éléments quadrangulaires et triangulaires dans les nœuds de coin sont les mêmes que pour les éléments 1D : degrés de liberté de déplacement (u_x, u_y, u_z) et de rotation (φ_x, φ_y, φ_z). Cela garantit la compatibilité entre les éléments 1D et 2D dans les nœuds. Les paramètres sont définis dans le système de coordonnées local des éléments et sont convertis dans le système de coordonnées global lors de la composition de la matrice de rigidité globale.

Éléments quadrangulaires pour les coques dans RFEM

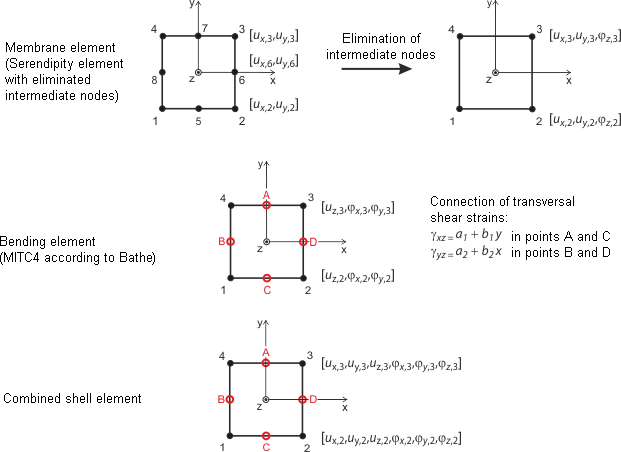
L'image Éléments quadrangulaires pour les coques affiche l'approche pour les éléments de coque plans. Elle est basée sur la théorie de Mindlin/Reissner. Pour qu'un couplage direct soit assuré avec les éléments de barre, une approche quadratique dans le plan de coque (u_x,u_y) est définie. En éliminant les nœuds intermédiaires, un élément à quatre nœuds est créé avec des degrés de liberté de rotation supplémentaires dans les directions x, y et z. Ainsi, un couplage direct avec des éléments de poutre est possible pour les éléments de diaphragme. À partir des interpolations combinées des déplacements transversaux, des rotations de section et des déformations dues au cisaillement transversal, les éléments MITC (interpolation mixte de composants en tension) de Bathe et DvorkinR[3] ont été utilisés : MITC3+ pour les triangles, MITC4 pour les quadrangles.

Les éléments de barre sont ici considérés par la résolution directe de l'équation différentielle selon l'analyse du second ordre. Considérer les effets de gauchissement n'est pas possible avec la torsion de Saint-Venant.

Les calculs de membrane sont basés sur les principes de Bergan [4] [5] [6]. Par exemple, pour des éléments triangulaires, les fonctions de base sont divisées en trois déformations rigides, trois conditions de déformation constante et trois gradients linéaires spéciaux de contrainte et de déformation. Le champ de déformation dans un élément est quadratique et le champ de contrainte est linéaire. La matrice de rigidité des éléments K_L est ensuite transformée en neuf paramètres collectifs des types u_x, u_y, φ_z. Les composants de cette matrice sont insérés avec les composants pour la flexion et le cisaillement dans la matrice de rigidité globale (18, 18). Cette matrice est le résultat du concept de Lynn-Dhillon. De cette manière, des plaques de Mindlin (plaques avec une déformation de cisaillement distincte) sont ainsi appliquées et analysées selon Timoshenko. RFEM trouve ainsi la solution adéquate pour les plaques épaisses et minces (plaques Navier).

Dans le cas de problèmes géométriquement non linéaires, la division mentionnée ci-dessus de la condition de contrainte-déformation à l'état plan et en flexion/cisaillement n'est pas possible. Les influences de ces états sont considérées dans la matrice K_NL. RFEM utilise une forme assez simple mais efficace de la matrice K_NL basée sur les approches de Zienkiewicz [7]. Le composant quadratique ε₂ du tenseur de déformation de Green/Lagrange ε = ε₁ + ε₂ est appliqué. Une distribution linéaire de u_z (x, y) des conditions de contraintes 2D et des distributions linéaires de u_x (x, y) et u_y (x, y) de l'interaction avec la flexion sont supposés. Cette supposition est possible car l'effet principal de l'interaction dépend de la première dérivation de l'équation différentielle. De plus, l'influence des composants d'ordre plus élévé diminue rapidement avec la division en plusieurs éléments. L'exactitude de cette procédure a été prouvée dans plusieurs analyses numériques.

Éléments 3D

Les éléments 3D sont utilisés pour les solides. Les types d'élément suivants sont implémentés dans RFEM : tétraèdre, pentaèdre (prisme, pyramide) et hexaèdre. Pour des informations détaillés à propos d'éléments et matrices, voir les « Éléments finis 3D avec degrés de liberté de rotation de Sevcik » [8]. Vous pouvez demander cette documentation à Dlubal Software.

Élément solide (hexaèdre)

En général, tous les degrés de liberté en rotation doivent être considérés comme critiques pour les solides. Comme la déformation d'un solide est déterminée uniquement à partir des vecteurs de déplacement, la rotation d'un nœud de maillage (due par exemple à une torsion introduite individuellement) n'affecte pas la déformation dans le solide.