Un appui de surface décrit le soutien de tous les éléments 2D d'une surface. Les déplacements de ces éléments peuvent être empêchés ou limités par des ressorts.
Base
L'onglet Base gère les paramètres élémentaires de l'appui.
Conditions d'appui
Les conditions d'appui sont divisées en degrés de liberté 'Translation' et 'Cisaillement'. Pour définir un soutien, cochez la case de contrôle pour l'axe concerné. La coche symbolise que le degré de liberté est verrouillé et que le déplacement de l'élément dans la direction de cet axe de surface n'est pas possible.
Si aucun soutien ni empêchement de cisaillement n'est présent, décochez la case de contrôle correspondante. La constante du ressort de déplacement ou de cisaillement sera alors réglée à zéro. Vous pouvez adapter la 'constante de ressort' à tout moment pour modéliser un appui élastique de la surface. Entrez les raideurs des ressorts comme valeurs de conception.
Les paramètres Cu,x et Cu,y représentent les ressorts de déplacement, décrivant la résistance de la fondation contre le déplacement dans les directions de la surface x et y. Pour une dalle de sol, vous pouvez ainsi définir la résistance (indépendante de la charge) dans les directions horizontales.
Les symboles d'appui sont toujours représentés sous la surface pour une surface horizontale ou inclinée (c'est-à-dire du côté de la direction de la gravité). Pour une surface verticale, l'orientation de l'axe de surface z est décisive. Une défaillance agit toutefois indépendamment de la représentation graphique : le critère de contrainte, basé sur l'orientation de l'axe z local, fait foi.
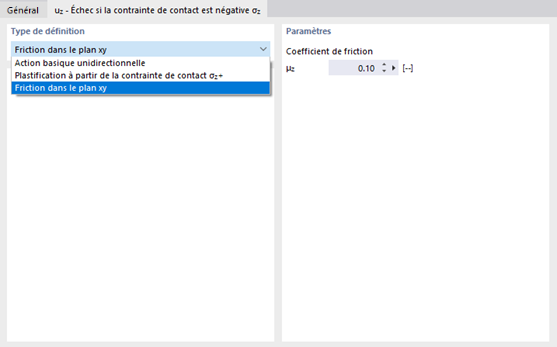
Pour la direction 'uz', il est possible de stipuler une non-linéarité (voir image Nouvel appui de surface). Le critère 'Défaillance si contrainte de contact σz négative ou positive' contrôle si l'appui peut seulement supporter des contraintes positives ou négatives. Vous pouvez définir d'autres paramètres de non-linéarité dans l'onglet uz - Défaillance si contrainte de contact σz négative ou positive.
Vérifiez l'orientation des axes z locaux lorsque vous appliquez un critère de défaillance. Vous pouvez activer et désactiver les axes de surface via le menu contextuel de la surface.
Les conditions d'appui pour le 'Cisaillement' vxz et vyz régulent comment la capacité de charge de cisaillement du soutien dans la direction des axes de surface x et y est prise en compte. La constante de Pasternak Cv se situe généralement entre 0,1 ⋅ Cu,z (faible capacité de charge de cisaillement) et 0,5 ⋅ Cu,z (capacité de charge de cisaillement moyenne). En règle générale, on considère : Cv,xz = Cv,yz.
Pour un appui inamovible en uz, les termes de cisaillement associés de la matrice de raideur sont automatiquement activés.
Le tableau suivant selon Kolar [1] propose des valeurs indicatives pour les constantes de ressort des sols.
| Consistance du sol | Cu,z [kN/m3] | Cv [kN] | Cv [kN] | Cv [kN] |
|---|---|---|---|---|
| minimal | moyen | élevé | ||
| très mou | 1 000 | 0 | 500 | 1 000 |
| moyennement dense | 10 000 | 0 | 5 000 | 10 000 |
| dense | 100 000 | 0 | 50 000 | 100 000 |
uz - Défaillance si contrainte de contact σz négative ou positive
La défaillance uz en tant que caractéristique non linéaire de l'appui de surface (voir image Nouvel appui de surface) peut être décrite plus en détail dans cet onglet.
La liste offre les choix suivants :
- Effet unilatéral fondamental : L'appui se défausse sous contraintes de contact négatives ou positives.
- Fluage à partir de la contrainte de contact : L'appui se défausse sous contraintes de contact négatives ou positives et n'est effectif dans l'autre domaine que jusqu'à une certaine contrainte. Au-delà, les déformations augmentent, mais non plus les contraintes.
- Friction dans le plan xy : L'appui se défausse sous contraintes de contact négatives ou positives. Les forces de cisaillement sont absorbées par friction. Elles dépendent des forces de contact existantes. La relation suivante s'applique : τ = μz ⋅ σ. L'appui dans les directions x et y n'est totalement pris en compte que lorsque la contrainte de contact τ est atteinte. Cela signifie qu'un appui rigide ou élastique dans les directions horizontales x et y doit également être défini. Sans cet appui, aucune friction dans le plan n'est active.