A surface support describes the support of all 2D elements of a surface. Displacements of these elements can be prevented or limited by translational springs.
Base
The Main tab manages the basic support parameters.
Support Conditions
The support conditions are divided into "Translational" and "Shear" degrees of freedom. To define a support, select the check box for the respective axis. The check mark indicates that the degree of freedom is locked and the displacement of the element in the direction of this surface axis is impossible.
If there is no support or shear restraint available, clear the corresponding check box. Then, the constant of the translational or shear spring is set to zero. You can adjust the "Spring constant" anytime in order to model an elastic support of the surface. Enter the spring stiffnesses as design values.
The parameters Cu,x and Cu,y represent translational springs that describe the foundation's resistance against displacement in the surface directions x or y. In the case of a floor slab, you can use them to define the (load-independent) resistance in the horizontal directions.
When the surface is horizontal or inclined, the support symbols are always displayed under the surface (that is, on the side in the direction of gravity). In the case of a vertical surface, the orientation of the surface axis z is governing. The Failure, however, acts independently of the graphical display: Hier entscheidet das Spannungskriterium, welches auf die Orientierung der lokalen z-Achse bezogen ist.
It is possible to specify a "Nonlinearity" for the uz direction (see the image New Surface Support). The criterion "Failure if negative or positive contact stress σz" controls whether the support can only absorb positive or negative forces. You can define further nonlinearity parameters in the uz – Failure if negative or positive contact stress σz tab.
Check the orientation of the local z-axes when applying failure criteria. You can display and hide the surface axes using the surface shortcut menu.
The support conditions for "Shear" vxz and vyz control how the shear resistance of the support in the direction of the surface axes x and y is taken into account. In most cases, the Pasternak constant Cv is between 0.1 ⋅ Cu,z (low shear resistance) and 0.5 ⋅ Cu,z (average shear resistance). In general, the following applies: Cv,xz = Cv,yz.
In the case of a support rigidly fixed in uz, the corresponding shear elements for the stiffness matrix are activated automatically.
The following table according to Kolar [1] provides orientation values for support spring constants of soils.
| Soil Consistence | Cu,z [kN/m3] | Cv [kN] | Cv [kN] | Cv [kN] |
|---|---|---|---|---|
| minimum | medium | high | ||
| very soft | 1,000 | 0 | 500 | 1,000 |
| medium dense | 10,000 | 0 | 5,000 | 10,000 |
| dense | 100,000 | 0 | 50,000 | 100,000 |
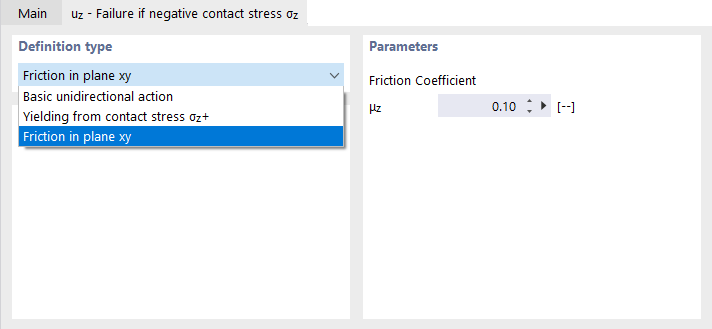
uz – Failure if negative or positive contact stress σz
In this tab, uz – Failure as a nonlinear property of the surface support (see the image New Surface Support) can be described in detail.
The list offers the following options:
- Basic unidirectional action: The support fails in the case of negative or positive contact stresses.
- Yielding from contact stress: The support fails in the case of negative or positive contact stresses and is effective in the other area only up to a certain stress. If it is exceeded, strains still increase, but not the stresses.
- Friction in plane xy: The support fails in the case of negative or positive contact stresses. Shear forces are absorbed by friction. They depend on the existing contact forces. The following relation applies: τ = μz ⋅ σ