Retour aux manuels en ligne

1740x

000483

27.04.2023

Sélectionner le Manuel

Aperçu

Interface graphique utilisateur et paramètres

Dlubal Center

Modèle - Données de base

Structure

Imperfections

Cas de charge et combinaisons

Assistants de charge

Charges

Calcul

Résultats

Objets repères

Fonctionnalités du programme

Évaluation des résultats

Rapports d'impression

Résultats par solide

Vous pouvez afficher graphiquement les résultats des solides à l'aide de la catégorie Solides du navigateur. Les résultats numériques des solides se trouvent dans la catégorie de tableau Résultats par solide.

Résultats par solide dans le tableau

Informations

Le tableau et le graphique montrent les résultats disponibles sur les surfaces aux limites du solide. Pour vérifier les résultats à l'intérieur du solide, sélectionnez l'option Sur les points du maillage EF dans la catégorie inférieure Valeurs sur les surfaces. Vous pouvez ensuite lire les valeurs dans le solide à l'aide d'un plan de coupe (voir le chapitre Plan de coupe).

Déformations

L'image Résultats par solide dans le tableau affiche le tableau avec les déformations des surfaces aux limites. Les déplacements et les rotations sont affichés dans les points de grille de surface (voir le chapitre Surfaces ).

Astuce

Pour les petites surfaces, le maillage standard de la grille de 0,5 m peut signifier qu'il n'existe que quelques points de grille. Dans ce cas, ajustez le nombre ou la distance des points de grille à la taille de la surface.

Les déformations ont la signification suivante :

	u	Valeur absolue du déplacement total
u_X	Déplacement en direction de l'axe global X
u_Y	Déplacement en direction de l'axe global Y
u_Z	Déplacement en direction de l'axe global Z
φ_X	Rotation autour de l'axe global X
φ_Y	Rotation autour de l'axe global Y
φ_Z	Rotation autour de l'axe global Z

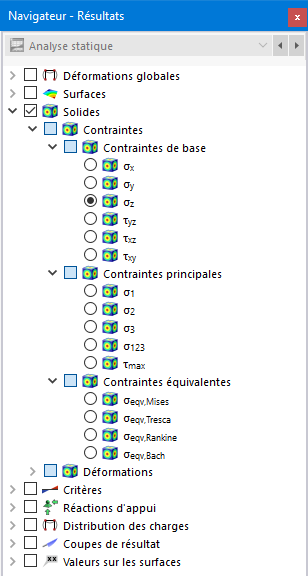
Contraintes

Sélection des contraintes de solides dans le navigateur

Contraintes des solides dans le tableau

Dans le navigateur, définissez les contraintes à afficher sur les surfaces aux limites des solides. Le tableau répertorie les contraintes de ces surfaces selon les spécifications spécifiées dans le Gestionnaire du tableau de résultats .

Les contraintes du solide sont réparties dans les catégories suivantes :

Contraintes de base
Contraintes principales
Contraintes équivalentes

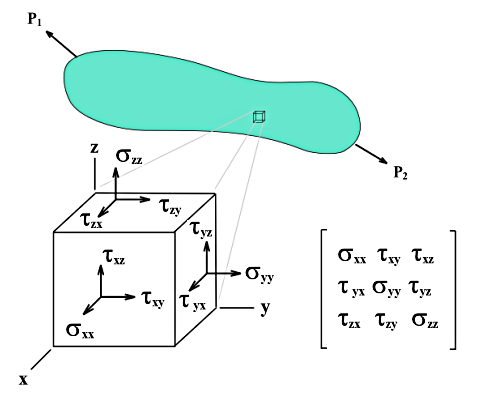
Contrairement aux contraintes de surface, les contraintes de solide ne peuvent pas être décrites par des équations simples. Les Contraintes de base σ_x, σ_y et σ_z, y compris les contraintes de cisaillement τ_yz, τ_xz et τ_xy sont déterminées directement par le noyau de calcul.

Si un cube avec des côtés de longueur d_x, d_y et d_z est extrait d'un objet 3D avec chargement multi-axial, les contraintes dans chaque surface cubique peuvent être divisées en contraintes normales et de cisaillement. Si ni la force spatiale, ni les différences de contrainte sur les surfaces parallèles ne sont considérées, la condition de contrainte dans le système de coordonnées local du cube peut être décrite par neuf composants de contrainte.

Volumenelement mit Spannungskomponenten

La matrice du tenseur de contrainte est la suivante :

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matrice du tenseur des contraintes

Les Contraintes principales σ₁, σ₂ et σ₃ résultent des valeurs propres du torseur comme suit :

\det (S - σ E) = 0

E	Matrice unitaire 3x3

Contraintes principales

La contrainte de cisaillement_maximale τmax est déterminée selon le cercle de Mohr' :

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Contrainte maximale de cisaillement

Astuce

Avec l'entrée σ₁₂₃ du navigateur, vous pouvez afficher graphiquement les trajectoires des contraintes principales.

Les contraintes équivalentes σ_v selon von Mises peuvent être déterminées par deux formules équivalentes.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Contrainte équivalente σ_{v, Mises} à partir des contraintes principales

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Contrainte équivalente σ_v,Mises à partir des contraintes de base

Pour déterminer la contrainte équivalente σ_v selon Tresca , les différences par rapport aux contraintes principales sont examinées afin de déterminer la valeur maximale.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Contrainte équivalente σ_v,Tresca

La contrainte équivalente σ_v selon Rankine est déterminé à partir des valeurs absolues les plus élevées des contraintes principales.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Contrainte équivalente_{v, Rankine}

Pour déterminer la contrainte équivalente σ_v selon Bach , les différences de contraintes principales sont examinées en tenant compte du coefficient de Poisson afin de déterminer la valeur maximale.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Contrainte équivalente_{v, Bach}

Déformations

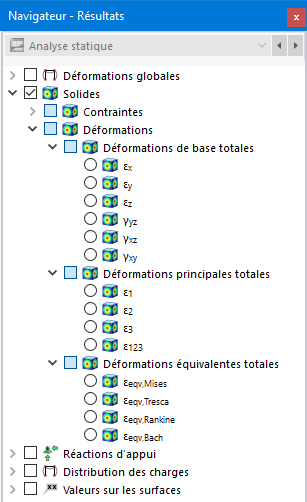
Sélection des déformations de solides dans le navigateur

Déformations de solides dans le tableau

Dans le navigateur, définissez les déformations à afficher sur les surfaces aux limites des solides. Le tableau répertorie les déformations de ces surfaces selon les spécifications du Gestionnaire du tableau de résultats .

Les déformations du solide sont réparties dans les catégories suivantes :

Déformations de base totales
Déformations principales totales
Déformations équivalentes totales

Les Déformations de base totales, y compris les déformations de cisaillement, sont déterminées directement par le noyau de calcul. La définition générale du tenseur pour un état de déformation 3D est la suivante :

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tenseur pour l'état de déformation

Les éléments du tenseur sont définis comme suit :

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Éléments tenseurs

Les Déformations principales totales ε₁, ε₂ et ε₃ sont déterminées à partir des déformations de base.

Astuce

Avec l'entrée ε₁₂₃ du navigateur, vous pouvez afficher graphiquement les trajectoires des principales déformations.

Les déformations équivalentes totales ε_v sont déterminées selon quatre hypothèses de contrainte :

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Déformation totale comparative ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

r	Matrice (voir ci-dessous)

Vergleichsgesamtdehnung ε_v,Tresca (Maximum der Eigenwertdifferenzen gemäß Matrix R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

r	Matrice (voir ci-dessous)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matrice (voir ci-dessous)

Déformation totale comparative ε_v,Bach (Différences de valeurs propres maximales selon la matrice R avec prise en compte du coefficient de Poisson ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matrice R

Chapitre parent

Résultats