Volver a manuales en línea

1740x

000483

2023-04-27

Seleccionar manual

Visión de conjunto

Interfaz gráfica de usuario y configuración

Centro de Dlubal

Datos básicos del modelo

Estructura

Imperfecciones

Casos de carga y combinaciones

Asistentes para cargas

Cargas

Cálculo

Resultados

Objetos auxiliares

Funciones del programa

Evaluación de resultados

Informes

Resultados por sólido

Puede mostrar los resultados para sólidos gráficamente utilizando la categoría del navegador Sólidos. Los resultados numéricos de los sólidos se encuentran en la categoría de tabla Resultados por sólido.

Resultados por sólido en la tabla

Información

Tanto la tabla como el gráfico muestran los resultados disponibles en las superficies de contorno del sólido. Para comprobar los resultados dentro del sólido, active la opción En puntos de malla de EF en la categoría Valores en superficies en la sección inferior del navegador. Luego, puede leer los valores dentro del sólido utilizando un plano de recorte (consulte el capítulo Planos de recorte).

Deformaciones

La imagen Resultados por sólido en la tabla muestra la tabla con las deformaciones de las superficies de contorno. Los desplazamientos y giros se muestran en los puntos de rejilla de la superficie (ver Capítulo Superficies ).

Consejo

Para superficies pequeñas, el tamaño de malla estándar de la rejilla de 0.5 m puede llevar al hecho de que solo existan unos pocos puntos de rejilla. En este caso, ajuste el número o la distancia de los puntos de la rejilla al tamaño de la superficie.

Las deformaciones tienen el siguiente significado:

\|u\|	Valor absoluto del desplazamiento total
u_X	Desplazamiento en dirección del eje X global
u_Y	Desplazamiento en dirección del eje Y global
u_Z	Desplazamiento en dirección del eje Z global
φ_X	Giro respecto al eje X global
φ_Y	Giro respecto al eje Y global
φ_Z	Giro respecto al eje Z global

Tensión

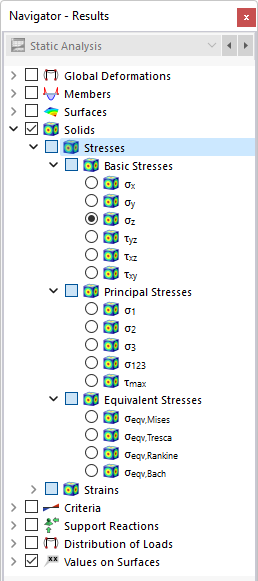
Selección de tensiones de sólidos en el navegador

Tensiones de sólidos en tabla

En el navegador, defina las tensiones que se mostrarán en las superficies de contorno de los sólidos. La tabla enumera las tensiones de estas superficies según las especificaciones establecidas en el Administrador de tablas de resultados .

Las tensiones en sólido se dividen en las siguientes categorías:

Tensiones básicas
Tensiones principales
Tensiones equivalentes

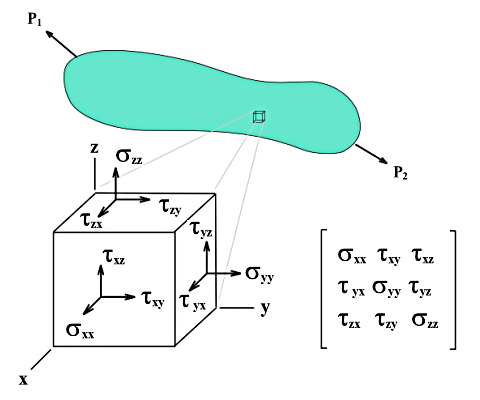
A diferencia de las tensiones de la superficie, las tensiones de los sólidos no se pueden describir mediante ecuaciones simples. Las tensiones básicas σx_, σy_y_σz, incluidas las tensiones tangenciales_τyz,_τxz y_τxy, se determinan directamente mediante el núcleo de análisis.

Si un cubo con longitudes de borde d_x, d_y, y d_z se corta a partir de un objeto 3D con carga multiaxial, las tensiones en cada superficie cúbica se pueden dividir en tensiones normales y tangenciales. Si no se consideran diferencias ni de fuerza espacial ni de tensión en las superficies paralelas, la condición de tensión en el sistema local de coordenadas del cubo se puede describir mediante nueve componentes de tensión.

Elemento de un sólido con los componentes de la tensión

La matriz del tensor de tensiones es la siguiente:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matriz del tensor de tensiones

Las tensiones principales σ₁, σ₂ y σ₃ resultan de los valores propios del tensor como sigue:

\det (S - σ E) = 0

E	Matriz unidad 3x3

Tensiones principales

La tensión tangencial_máxima τmax se determina según el círculo de Mohr':

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Tensión tangencial máxima

Consejo

Con la entrada del navegador σ₁₂₃ puede mostrar gráficamente las trayectorias de las tensiones principales.

Las tensiones equivalentes_σv según von Mises se puede determinar mediante dos fórmulas equivalentes.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Tensión equivalente σ_v,Mises de las tensiones principales

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Tensión equivalente σ_v,Mises de las tensiones básicas

Para determinar la tensión equivalente σ_v según Tresca , se examinan las diferencias con las tensiones principales a fin de determinar el valor máximo.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Tensión equivalente σ_v,Tresca

La tensión equivalente σ_v según Rankine se determina a partir de los mayores valores absolutos de las tensiones principales.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Tensión equivalente σ_v,Rankine

Para determinar la tensión equivalente σ_v según Bach , se examinan las diferencias entre tensiones principales considerando el coeficiente de Poisson a fin de determinar el valor máximo.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Tensión equivalente σ_v,Bach

deformaciones

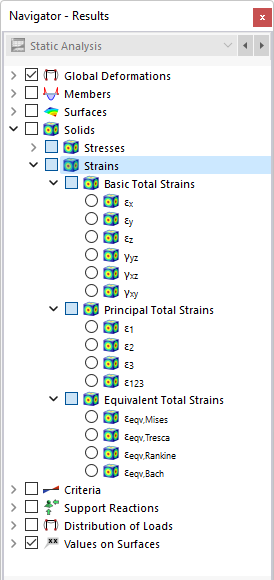
Selección de deformaciones de sólidos en el navegador

Deformaciones en sólidos en la tabla

En el navegador, defina las deformaciones que se mostrarán en las superficies de contorno de los sólidos. La tabla enumera las deformaciones de estas superficies según las especificaciones establecidas en el Administrador de tablas de resultados .

Las deformaciones en sólido se dividen en las siguientes categorías:

Deformaciones totales básicas
Deformaciones totales principales
Deformaciones totales equivalentes

Las deformaciones totales básicas, junto con las deformaciones tangenciales, las determina directamente el núcleo de cálculo. La definición general del tensor para el estado de la deformación espacial es la siguiente:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tensor para el estado de deformación

Los elementos del tensor se definen de la siguiente manera:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Elementos tensores

Las deformaciones totales principales ε₁, ε₂ y ε₃ se determinan a partir de las deformaciones básicas.

Consejo

La entrada del navegador ε₁₂₃ le permite mostrar gráficamente las trayectorias de las deformaciones principales.

Las deformaciones totales equivalentes ε_v se determinan según cuatro hipótesis de tensión diferentes como a continuación.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Deformación total comparativa ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matriz (ver a continuación)

Deformación total comparativa ε_v,Tresca (la máxima diferencia entre valores propios según la matriz R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matriz (ver a continuación)

Deformación total comparativa ε_v,Rankine (la máxima diferencia entre valores propios según la matriz R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matriz (ver a continuación)

Deformación total comparativa ε_v,Bach (la máxima diferencia entre valores propios según la matriz R considerando el coeficiente de Poisson ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matriz R

Capítulo principal

Resultados