Powrót do Instrukcji online

1740x

000483

2023-04-27

Wybór ręczny

Przegląd

Graficzny interfejs użytkownika i jego ustawienia

Centrum Dlubal

Dane podstawowe modelu

Konstrukcja

Imperfekcje

Przypadki obciążeń i kombinacje

Generatory obciążeń

Obciążenia

Obliczenia

Wyniki

Obiekty pomocnicze

Funkcje programu

Analiza wyników

Raporty z obliczeń

Wyniki według brył

Wyniki dla brył można wyświetlić graficznie za pomocą kategorii nawigatora Bryły. Wyniki numeryczne brył można znaleźć w kategorii tabeli Wyniki według bryły.

Wyniki w tabeli według brył

Informacje

Zarówno w tabeli, jak i na rysunku przedstawiono wyniki dostępne na powierzchniach granicznych bryły. Aby sprawdzić wyniki wewnątrz bryły, należy aktywować opcję Na punktach siatki ES w kategorii Wartości na powierzchniach w dolnej sekcji nawigatora. Następnie wartości w bryle można odczytać za pomocą płaszczyzny przycinania (patrz rozdział Płaszczyzny przycinania).

osnowa

Rysunek Wyniki w tabeli według brył przedstawia tabelę z odkształceniami powierzchni granicznych. W punktach rastra powierzchni wyświetlane są przemieszczenia i obroty (patrz rozdział Powierzchnie ).

Wskazówka

W przypadku małych powierzchni 'standardowy rozmiar oczek rastra wynoszący 0,5 m może powodować, że istnieje tylko kilka punktów rastra. W takiej sytuacji należy dostosować liczbę lub rozstaw punktów rastra do rozmiaru powierzchni.

Odkształcenia mają następujące znaczenie:

	u	Bezwzględna wartość całkowitego przemieszczenia
u_X	Przemieszczenie w kierunku globalnej osi X
u_Y	Przemieszczenie w kierunku globalnej osi Y
u_Z	Przemieszczenie w kierunku globalnej osi Z
φ_X	Obrót wokół globalnej osi X
φ_Y	Obrót wokół globalnej osi Y
φ_Z	Obrót wokół globalnej osi Z

Naprężenie

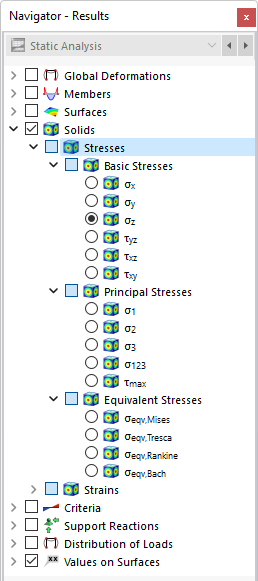
Wybór naprężeń w bryle w Nawigatorze

Naprężenia brył w tabeli

W nawigatorze należy zdefiniować naprężenia, które mają być wyświetlane na powierzchniach granicznych brył. W tabeli wyszczególnione są naprężenia tych powierzchni zgodnie ze specyfikacjami zawartymi w Menedżer tabeli wyników .

Naprężenia w bryłach są podzielone na następujące kategorie:

Naprężenia podstawowe
Naprężenia główne
Naprężenia równoważne

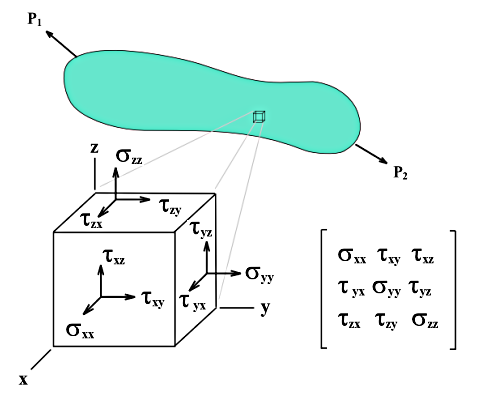
W przeciwieństwie do naprężeń powierzchni naprężeń brył nie można opisać za pomocą prostych równań. Naprężenia podstawowe σ_x, σ_y i σ_z wraz z naprężeniami ścinającymi τ_yz, τ_xz i τ_xy są bezpośrednio określane przez rdzeń analizy.

Jeżeli z bryły obciążonej wieloosiowo zostanie wycięty sześcian o długościach boków d_x, d_y i d_z,naprężenia w każdej powierzchni sześcianu można rozłożyć na naprężenia normalne i ścinające. Przy pominięciu siły objętościowej oraz różnic między naprężeniami na powierzchniach równoległych można opisać stan naprężenia w lokalnym układzie współrzędnych sześcianu za pomocą dziewięciu składowych naprężenia.

Volumenelement mit Spannungskomponenten

Macierz tensora naprężeń ma postać:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Macierz tensora naprężeń

Naprężenia główne σ₁, σ₂ i σ₃ wynikają z wartości własnych tensora w następujący sposób:

\det (S - σ E) = 0

E	Macierz jednostkowa 3x3

Naprężenia główne

Maksymalne naprężenie styczne τ_max jest określane według okręgu Mohra'sa:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Max naprężenie styczne

Wskazówka

Pozycja σ₁₂₃ w nawigatorze umożliwia graficzne przedstawienie trajektorii naprężeń głównych.

Naprężenia równoważne σ_v wg von Misesa można wyznaczyć za pomocą dwóch równoważnych wzorów.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Naprężenie równoważne σ_{v, Mises} z naprężeń głównych

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Naprężenie równoważne σ_v,Mises z naprężeń podstawowych

Aby określić naprężenie równoważne σ_v zgodnie z Tresca , sprawdzane są różnice między naprężeniami głównymi w celu określenia wartości maksymalnej.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Naprężenie równoważne σ_{v, Tresca}

Naprężenie równoważne σ_v wg Rankine jest określany na podstawie największych wartości bezwzględnych naprężeń głównych.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Naprężenie równoważne σ_v,Rankine

Aby określić naprężenie równoważne σ_v zgodnie z Bach , sprawdzane są główne różnice naprężeń z uwzględnieniem współczynnika Poissona ν, w celu wyznaczenia wartości maksymalnej.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Naprężenie równoważne σ_{v, Bach}

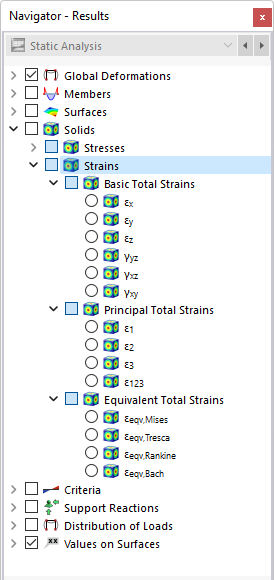
odkształcenia

Wybór odkształceń w bryłach w Nawigatorze

Odkształcenia na bryłach w tabeli

W nawigatorze należy zdefiniować odkształcenia, które mają być wyświetlane na powierzchniach granicznych brył. W tabeli wyszczególnione są odkształcenia tych powierzchni zgodnie ze specyfikacjami zawartymi w Menedżer tabeli wyników .

Odkształcenia bryły dzielą się na następujące kategorie:

Podstawowe odkształcenia całkowite
Główne odkształcenia całkowite
Zastępcze odkształcenia całkowite

Podstawowe odkształcenia całkowite wraz z odkształceniami przy ścinaniu są określane bezpośrednio przez rdzeń obliczeń. Ogólna definicja tensora przestrzennego stanu odkształcenia brzmi: