Voltar para manuais online

1740x

000483

2023-04-27

Selecionar manual

Vista geral

Interface gráfica do utilizador e configurações

Dlubal Center

dados gerais do modelo

Estrutura

Imperfeições

Casos e combinações de carga

Assistentes de carga

Cargas

Cálculo

Resultados

Objetos auxiliares

Ferramentas

Avaliação dos resultados

Relatórios de impressão

Resultados por sólido

Os resultados para sólidos podem ser apresentados graficamente utilizando a categoria de navegador Sólidos. Pode encontrar os resultados numéricos para sólidos na categoria de tabela Resultados por sólido.

Resultados por sólido na tabela

Informação

Tanto a tabela como o gráfico apresentam os resultados disponíveis nas superfícies de fronteira do sólido. Para verificar os resultados no interior do sólido, active a opção Nos pontos da malha de EF na categoria Valores nas superfícies na secção inferior do navegador. Depois, pode ler os valores dentro do sólido utilizando um plano de corte (ver Capítulo Planos de corte).

Deformações

A imagem {%>#image026063 Resultados por sólido na tabela]] mostra a tabela com as deformações das superfícies de contorno. Os deslocamentos e rotações são exibidos nos pontos de grelha da superfície (ver Capítulo Superfícies ).

Sugestão

Para pequenas superfícies, o tamanho de malha padrão da grelha' de 0,5 m pode fazer com que existam apenas alguns pontos de grelha. Neste caso, ajuste o número ou a distância dos pontos de grelha ao tamanho da superfície.

As deformações tem o seguinte significado:

u Valor absoluto do deslocamento total

u_X Deslocamento na dirceção do eixo global X

u_Y Deslocamento na direcção do eixo global Y

u_Z Deslocamento na direcção do eixo global Z

φ_X Rotação sobre o eixo global X

φ_Y Rotação sobre o eixo global Y

φ_Z Rotação sobre o eixo global Z

Tensão

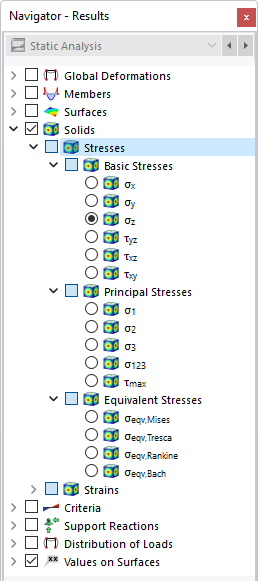
Seleção de tensões sólidas no navegador

Tensões de sólidos na tabela

No navegador, defina as tensões a serem exibidas nas superfícies de fronteira dos sólidos. A tabela lista as tensões destas superfícies de acordo com as especificações definidas no Gestor de tabela de resultados .

As tensões de sólido estão subdivididas nas seguintes categorias:

tensões básicas

Tensões principais

Tensões equivalentes

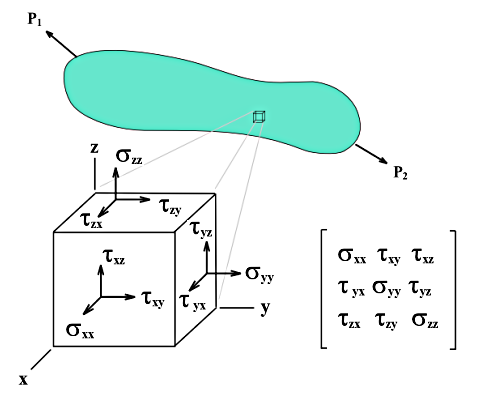
Ao contrário das tensões de superfície, as tensões de sólidos não podem ser descritas por equações simples. As Tensões básicas_{σx, σy, e σz incluindo as tensões de corte τ yz}_,_τ_xz_, e τ_xy são determinadas directamente pela análise principal.

Se um cubo com os comprimentos de ponta d_x, d_y, e d_z é cortado a partir de um objecto 3D com carregamento multiaxial, as tensões em cada superfície cúbica podem ser divididas em tensões normais e tensões de corte. Se nem a força espacial nem as diferenças de tensão nas superfícies paralelas forem consideradas, o estado de tensão no sistema de coordenadas local do cubo' pode ser descrito por nove componentes de tensão.

Volumenelement mit Spannungskomponenten

A matriz do tensor das tensões é o seguinte:

$S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]$

Matriz de tensor de tensão

As Tensões principais_σ1, σ2 e_σ3 resultam dos valores próprios do tensor como se segue_:

$\det (S - σ E) = 0$

E Matriz de unidades 3x3

Tensões principais

A tensão de corte máxima τ_max é determinada de acordo com o círculo de Mohr's:

$τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})$

Tensão de corte máxima

Sugestão

A entrada do navegador σ₁₂₃ permite representar graficamente as trajectórias das tensões principais.

Tensões equivalentes σ_v de acordo com von Mises pode ser determinado através de duas fórmulas equivalentes.

$σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}$

Tensão equivalente σ_{v, Mises} de tensões principais

$σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}$

Tensão equivalente σ_{v, Mises} de tensões básicas

Para determinar a tensão equivalente σ_v segundo Tresca , são examinadas as diferenças em relação às tensões principais de forma a determinar o valor máximo.

$σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)$

Tensão equivalente σ_{v, Tresca}

Tensão equivalente σ_v de acordo com Rankine é determinado a partir dos valores absolutos maiores das tensões principais.

$σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)$

Tensão equivalente σ_{v, Rankine}

Para determinar a tensão equivalente σ_v segundo Bach , são examinadas as diferenças das tensões principais, tendo em consideração o coeficiente de Poisson's ν para determinar o valor máximo.

$σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]$

Tensão equivalente σ_{v, Bach}

deformações

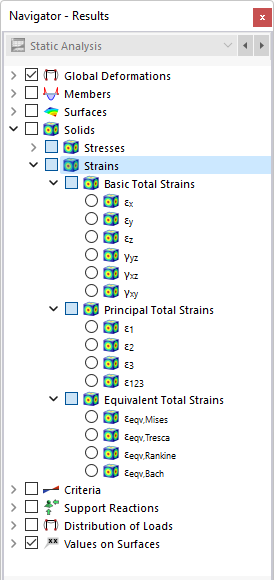
Seleção de deformações sólidas no Navegador

Deformações em sólidos na tabela

No navegador, define as deformações a serem exibidas nas superfícies de fronteira dos sólidos. A tabela lista as deformações destas superfícies de acordo com as especificações definidas no Gestor de tabela de resultados .

As deformações de sólidos estão divididas nas seguintes categorias:

Deformações totais de base

Deformações principais totais

Deformações totais equivalentes

As deformações totais de base incluindo as deformações por corte são determinadas diretamente pelo núcleo computacional. A definição geral do tensor para o estado das deformações espaciais é o seguinte:

$ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]$

Tensor para estado de deformação

Os elementos do tensor são definidos da seguinte forma:

$ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})$

Elementos tensores

As deformações principais totais ε₁, ε₂ e ε₃ são determinadas a partir das deformações de base.

Sugestão

A entrada do navegador ε₁₂₃ permite-lhe apresentar graficamente as trajectórias das deformações principais.

As deformações totais equivalentes ε_v são determinadas de acordo com quatro diferentes hipóteses de tensões como se segue.

$ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}$

Deformação total comparativa ε_{v, Mises}

$ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)$

[SCHOOL.REQUESTORCALLBACK] Matriz (ver abaixo)

Vergleichsgesamtdehnung ε_v,Tresca (Maximum der Eigenwertdifferenzen gemäß Matrix R)

$ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)$

[SCHOOL.REQUESTORCALLBACK] Matriz (ver abaixo)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

$ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)$

[SCHOOL.REQUESTORCALLBACK] Matriz (ver abaixo)

Deformação total comparativa ε_{v, Bach} (máximo das diferenças de valores próprios de acordo com a matriz R, tendo em conta a relação de Poisson ' s ν)

$R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]$

Matrix R

Capítulo principal

Resultados

	u	Valor absoluto do deslocamento total
u_X	Deslocamento na dirceção do eixo global X
u_Y	Deslocamento na direcção do eixo global Y
u_Z	Deslocamento na direcção do eixo global Z
φ_X	Rotação sobre o eixo global X
φ_Y	Rotação sobre o eixo global Y
φ_Z	Rotação sobre o eixo global Z