Torna a Manuali online

1740x

000483

2023-04-27

Seleziona il manuale

Panoramica

Interfaccia grafica utente e impostazioni

Dlubal Center

Dati di base del modello

Struttura

Imperfezioni

Casi e combinazioni di carico

Creazioni guidate di carichi

Carichi

Calcolo

Risultati

Oggetti di aiuto

Strumenti

Valutazione dei risultati

Relazioni di calcolo

Risultati per solido

È possibile visualizzare graficamente i risultati per i solidi utilizzando la categoria del navigatore Solidi. I risultati numerici dei solidi si trovano nella categoria della tabella Risultati per solido.

Risultati per solido nella tabella

Informazione

Sia la tabella che il grafico mostrano i risultati disponibili sulle superfici al contorno del solido. Per verificare i risultati all'interno del solido, attivare l'opzione Sui punti della mesh EF nella categoria Valori sulle superfici nella sezione del navigatore inferiore. Quindi, è possibile leggere i valori all'interno del solido utilizzando un piano di ritaglio (vedere il capitolo Piani di ritaglio).

Ordito

L'immagine Risultati per solido nella tabella mostra la tabella con gli spostamenti generalizzati delle superfici al contorno. Gli spostamenti e le rotazioni sono visualizzati nei punti della griglia della superficie (vedi Capitolo Superfici ).

Suggerimento

Per piccole superfici, la dimensione della mesh standard della griglia di 0,5 m può causare solo pochi punti della griglia. In questo caso, regolare il numero o la distanza dei punti della griglia alle dimensioni della superficie.

Gli spostamenti generalizzati hanno il seguente significato:

	u	Valore assoluto dello spostamento totale
u_X	Spostamento in direzione dell'asse globale X
u_Y	Spostamento in direzione dell'asse globale Y
u_Z	Spostamento in direzione dell'asse globale Z
φ_X	Rotazione attorno all'asse globale X
φ_Y	Rotazione attorno all'asse globale Y
φ_Z	Rotazione attorno all'asse globale Z

Tensione

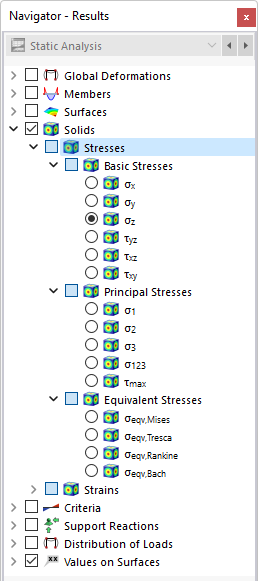
Selezione delle tensioni dei solidi nel Navigatore

Tensioni dei solidi nella tabella

Nel navigatore, definisci le tensioni da visualizzare sulle superfici al contorno dei solidi. La tabella elenca le tensioni di queste superfici secondo le specifiche impostate nel Gestore tabelle dei risultati .

Le tensioni dei solidi sono suddivise nelle seguenti categorie:

tensioni di base
Tensioni principali
Tensioni equivalenti

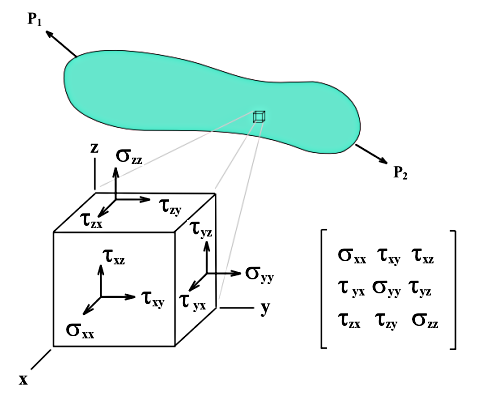
Diversamente dalle tensioni delle superfici, le tensioni dei solidi non possono essere descritte con semplici equazioni. Le tensioni di base σ_x, σ_y e σ_z comprese le tensioni tangenziali τ_yz, τ_xz e τ_xy sono determinate direttamente dal nucleo dell'analisi.

Se un cubo con le lunghezze dei bordi d_x, d_y e d_z viene tagliato da un oggetto 3D con carico multiassiale, le tensioni in ciascuna superficie cubica possono essere suddivise in normali e tangenziali. Se non si prendono in considerazione né la forza spaziale né le differenze di tensione su superfici parallele, la condizione tensionale nel sistema di coordinate locali del cubo possono essere descritte da nove componenti.

Volumenelement mit Spannungskomponenten

La matrice del tensore della tensione è la seguente:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matrice del tensore delle tensioni

Le tensioni principali σ₁, σ₂ e σ₃ risultano dagli autovalori del tensore come segue:

\det (S - σ E) = 0

E	Matrice di unità 3x3

Tensioni principali

La tensione tangenziale massima τ_max è determinata secondo il cerchio di Mohr's:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Massima tensione tangenziale

Suggerimento

La voce del navigatore σ₁₂₃ consente di visualizzare graficamente le traiettorie delle tensioni principali.

Le tensioni equivalenti σ_v secondo von Mises può essere determinato con due formule equivalenti.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Tensione equivalente σ_v,Mises dalle tensioni principali

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Tensione equivalente σ_v,Mises dalle tensioni di base

Per determinare la tensione equivalente σ_v secondo Tresca , vengono esaminate le differenze dalle tensioni principali per determinare il valore massimo.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Tensione equivalente_{v, Tresca}

La tensione equivalente σ_v secondo Rankine è determinato dai massimi valori assoluti delle tensioni principali.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Tensione equivalente_{v, Rankine}

Per determinare la tensione equivalente σ_v secondo Bach , vengono esaminate le principali differenze di tensione, tenendo conto del rapporto di Poisson's ν, al fine di determinare il valore massimo.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Tensione equivalente_{v, Bach}

deformazioni

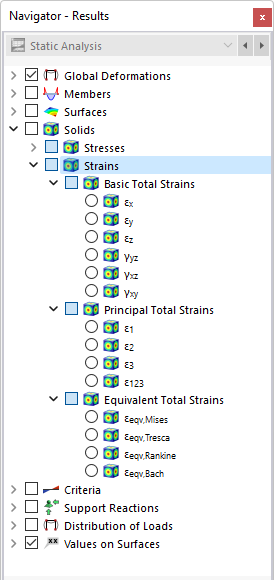
Selezione di deformazioni solide nel Navigatore

Deformazioni sui solidi nella tabella

Nel navigatore, definisci le deformazioni da visualizzare sulle superfici al contorno dei solidi. La tabella elenca le deformazioni di queste superfici secondo le specifiche impostate nel Gestore tabelle dei risultati .

Le deformazioni dei solidi sono suddivise nelle seguenti categorie:

Deformazioni totali di base
Deformazioni totali principali
Deformazioni totali equivalenti

Le deformazioni totali di base comprese le deformazioni a taglio sono determinate direttamente dal kernel di calcolo. La definizione generale del tensore per lo stato di deformazione spaziale è la seguente: