Un'impostazione di analisi statica ( SA ) specifica le regole in base alle quali vengono calcolati i casi di carico e le combinazioni di carico. Sono preimpostati tre tipi di analisi standard.
Principale
La scheda Principale gestisce le impostazioni per l'analisi strutturale e i parametri di calcolo elementari.
Tipo di analisi
Questa sezione di dialogo controlla la teoria di calcolo in base alla quale vengono analizzati i casi di carico e le combinazioni di carico. Nell'elenco 'Tipo di analisi', sono disponibili tre approcci per la selezione.
Lineare geometricamente
Quando si calcola secondo l'analisi geometricamente lineare (primo ordine), l'equilibrio viene analizzato su un sistema strutturale indeformato. Viene eseguita un'analisi lineare perché le deformazioni dei componenti non sono incluse nel calcolo.
I casi di carico sono calcolati in base all'analisi geometricamente lineare per impostazione predefinita.
Secondo ordine (P-Δ)
Nell'analisi "strutturale" del secondo ordine, l'equilibrio è determinato su un sistema strutturale deformato. Si presuppone che gli spostamenti generalizzati siano piccoli. Le forze assiali nel sistema hanno un impatto sull'aumento dei momenti flettenti. Pertanto, questa analisi ha effetto quando le forze assiali sono significativamente maggiori delle forze di taglio.
Le combinazioni di carico sono calcolate in modo non lineare per impostazione predefinita secondo l'analisi del secondo ordine.
Grandi spostamenti
L'analisi delle grandi deformazioni (terzo ordine o teoria delle grandi deformazioni) considera le forze longitudinali e trasversali nel calcolo. Dopo ogni fase di iterazione, viene creata la matrice di rigidezza di un sistema deformato. I carichi sono movimentati in modo differenziato: Un carico definito nella direzione globale mantiene la sua direzione se gli elementi finiti sono attorcigliati. Se il carico agisce nella direzione di un'asta locale o dell'asse della superficie, cambia la sua direzione in base alla torsione dell'elemento's.
Se il modello include aste del cavo, il calcolo secondo l'analisi di grandi deformazioni è preimpostato.
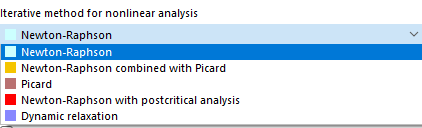
Metodo iterativo per analisi non-lineare
A seconda del tipo di analisi, sono disponibili vari metodi per risolvere il sistema algebrico di equazioni non lineare.
Newton-Raphson
Il metodo secondo Newton-Raphson è quello predefinito per analisi a grandi spostamenti. Il sistema di equazioni non lineari si risolve numericamente utilizzando delle approssimazioni iterative alle tangenti. La matrice di rigidezza tangenziale è determinata in funzione dello stato di deformazione attuale; è invertito in ogni ciclo di iterazioni. Nella maggior parte dei casi, si raggiunge velocemente una convergenza (quadratica).
Newton-Raphson combinato con Picard
L'approccio secondo Picard viene applicato per primo. Dopo alcune iterazioni, si passa al metodo Newton-Raphson. L'idea di base di questo approccio è utilizzare il metodo Picard relativamente "insensibile" per i primi passaggi dell'iterazione al fine di evitare messaggi di instabilità. A questa approssimazione iniziale segue un metodo veloce secondo il metodo di Newton-Raphson per trovare lo stato ultimo di equilibrio.
Picard
Il metodo secondo Picard, noto anche come metodo delle secanti, può essere inteso come un'approssimazione alle differenze finite del metodo Newton-Raphson. Viene considerata la differenza tra la corrente e l'iterazione originale eseguita nella fase di incremento del carico corrente. Spesso, la conversione è più lenta del metodo di calcolo secondo Newton-Raphson. Tuttavia, si rivela anche meno sensibile ai problemi non lineari, il che rende il calcolo più stabile.
Newton-Raphson con analisi post-critica
Questo metodo è utile per risolvere problemi post-critici in cui è presente una serie di instabilità da superare. Se è disponibile un'instabilità e la matrice di rigidezza non può essere invertita, viene utilizzata la matrice di rigidezza dell'ultimo passaggio di iterazione stabile. Il calcolo con la matrice viene continuato fino a quando non si raggiunge nuovamente un intervallo di stabilità.
Rilassamento dinamico
Il metodo finale è adatto per i calcoli secondo l'analisi di grandi deformazioni e per la risoluzione di problemi relativi ai problemi post-critici. In questo approccio, viene introdotto un parametro di tempo artificiale. Tenendo conto dell'inerzia e dello smorzamento, il cedimento può essere gestito come un problema dinamico. Questo approccio utilizza il metodo dell'integrazione temporale esplicita; la matrice di rigidezza non è invertita. Nessuna parte del modello può avere un peso specifico pari a zero quando si calcola con il rilassamento dinamico.
Questo metodo include anche lo smorzamento di Rayleigh che può essere definito mediante le costanti α e β secondo la seguente equazione con derivate temporali:
|
M |
Matrice di massa concentrata (diagonale). |
|
C |
Matrice di smorzamento diagonale C = α M + βdiag[K11 ( u ),K22 ( u ),...,Knn ( u )] |
|
K |
Matrice di rigidezza |
|
f |
Vettore di forze esterne |
|
u |
Vettore di spostamento discretizzato |
Controlli per l'analisi non-lineare
Il 'Numero massimo di iterazioni' definisce quante esecuzioni di calcolo vengono eseguite al massimo per un'analisi secondo il secondo ordine o analisi di grandi deformazioni, nonché per oggetti ad azione non lineare. Quando il calcolo raggiunge il limite senza raggiungere un equilibrio, viene visualizzato un messaggio corrispondente. Quindi, puoi decidere se vuoi visualizzare i risultati.
Il 'Numero di incrementi di carico' è rilevante per i calcoli secondo il secondo ordine o analisi di grandi deformazioni. L'individuazione dell'equilibrio è spesso difficile quando si considerano grandi spostamenti generalizzati. Le instabilità possono essere evitate applicando il carico in più fasi. Ad esempio, se si specificano due incrementi di carico, la metà del carico viene applicata nel primo passaggio. Le iterazione saranno effettuate fino a quando non si raggiungerà l'equilibrio. Quindi, nella seconda fase, il carico completo viene applicato al sistema già deformato e le iterazioni vengono eseguite di nuovo fino al raggiungimento dell'equilibrio.
Opzioni I
In questa sezione di dialogo, puoi attivare varie 'impostazioni speciali' per manipolare i calcoli secondo il secondo ordine o analisi di grandi deformazioni.
Modifica impostazioni standard di precisione e tolleranza
Quando si seleziona la casella di controllo 'Modifica impostazioni di precisione e tolleranza standard', la scheda Precisione e tolleranza viene aggiunta alla finestra di dialogo. Qui è possibile modificare i criteri di convergenza.
Ignora tutte le non linearità
Con la casella di controllo 'Ignora tutte le non linearità', è possibile disattivare le proprietà non lineari degli elementi per il calcolo. Pertanto, le aste di trazione, ad esempio, rimangono nel modello non appena si verificano forze di compressione. Tuttavia, è necessario sopprimere le proprietà non lineari solo a scopo di verifica; ad esempio, per trovare la causa di un'instabilità. I criteri di errore definiti in modo errato sono talvolta responsabili di interruzioni nel calcolo.
Opzioni II
Modifica carico con coefficiente moltiplicativo
Dopo aver spuntato la casella di controllo, è possibile definire un coefficiente k per il quale devono essere moltiplicati tutti i carichi.
Le norme più vecchie avevano come obiettivo quello di moltiplicare i carichi globalmente per un determinato coefficiente per aumentare gli effetti secondo l'analisi del secondo ordine per progetti di stabilità. D'altro canto, il progetto deve essere effettuato con i carichi caratteristici. Entrambi i requisiti possono essere soddisfatti inserendo un coefficiente maggiore di 1 e attivando la casella di controllo 'Dividi i risultati per coefficiente di carico'.
Per le analisi secondo gli standard attuali, il carico non dovrebbe essere modificato tramite fattori. Invece, i coefficienti di sicurezza parziale e di combinazione devono essere presi in considerazione per la sovrapposizione nelle situazioni di progetto.
Considera effetto favorevole dovuto alla trazione nelle aste
Le forze di trazione hanno un effetto favorevole su sistemi strutturali pre-deformati. Pertanto, la deformazione è ridotta e la struttura è stabilizzata. Di solito, si beneficia di questo effetto nei calcoli secondo l'analisi di deformazione ampia e del secondo ordine; ad esempio, per capannoni con controventi o strutture generali soggette a flessione. Lo scarico dovuto agli effetti delle forze di trazione per travi reticolari dal basso (travi con tiranti o cavi) può comportare una riduzione indesiderata delle deformazioni e delle forze interne.
Verifica di stabilità in base alla velocità di deformazione
Se si seleziona la casella di controllo, RFEM controlla come si sviluppano le deformazioni nel corso delle iterazioni durante il calcolo. Se gli spostamenti o le rotazioni aumentano bruscamente e superano un limite interno del programma, il calcolo viene interrotto con un messaggio di instabilità.
Prova a calcolare la struttura instabile
Con questa casella di controllo, puoi provare a rendere calcolabile un modello instabile: Nella prima fase di calcolo, RFEM applica piccole molle stabilizzando il modello per la prima iterazione. Una volta raggiunto uno stato iniziale stabile, le molle vengono rimosse per le iterazioni successive.
Spostamenti dovuti al carico dell'asta di tipo 'Pressione interna del tubo'
La casella di controllo è rilevante per il carico dell'asta chiamato pressione interna del tubo. L'effetto Bourdon descrive lo sforzo di un tubo piegato per raddrizzarsi sotto l'influenza della pressione. Sia le tensioni perimetrali che le tensioni assiali causate dal carico di pressione interno portano a una deformazione longitudinale del tubo, considerando la rigidezza del materiale e la deformazione trasversale.
Vedi questo Technical Article che descrive un esempio di come viene calcolata la pressione interna dei tubi.
Salva risultati di tutti gli incrementi di carico
Se il carico viene applicato in modo incrementale (vedi Controlli per l'analisi non lineare), puoi utilizzare questa casella di controllo per forzare l'output dei risultati intermedi al fine di controllare i risultati dei singoli incrementi del carico.
Risolutore diretto asimmetrico
Un risolutore di equazioni dirette non simmetriche viene utilizzato per un modello di materiale non lineare (vedere il capitolo Comportamento non lineare del materiale) con proprietà asimmetriche per trazione e compressione. La casella di controllo consente di utilizzare questo risolutore di equazioni anche per altri modelli di materiale, come il modello di materiale elastico isotropo non lineare.
Equilibrio per struttura indeformata
La casella di controllo consente di analizzare una struttura indeformabile, ovvero un sistema strutturale le cui deformazioni rimangono zero. Questa opzione di analisi può essere utile quando un sistema è sottoposto a tensione, ad esempio a causa di un caso di carico, mentre le deformazioni risultanti possono essere considerate sbiadite.
Un campo di applicazione per il calcolo dell'equilibrio per la struttura indeformata è lo stato tensionale primario dell'analisi geotecnica. Nell'ambito di un caso di carico o di una combinazione, devono essere determinate le tensioni agenti risultanti dal precarico del terreno. Tuttavia, le deformazioni di tale caso o combinazione di carico non sono di interesse e quindi non sono oggetto di ulteriore utilizzo.
Impostazioni base
La scheda Impostazioni di base gestisce le specifiche di base per il calcolo.
Rapporto del carico permanente
La casella di controllo 'Determina per combinazioni di carico' offre la possibilità di determinare il rapporto di un carico permanente in una combinazione di carico. Selezionare la combinazione di carico nell'elenco o creare una nuova combinazione di carico con il pulsante
![]() . Quindi, nell'elenco 'Confronta valore risultato', puoi definire i rapporti che hanno un effetto statico o variabile.
. Quindi, nell'elenco 'Confronta valore risultato', puoi definire i rapporti che hanno un effetto statico o variabile.
Il rapporto tra il carico permanente può essere considerato conforme alle norme nel progetto.
Metodo del sistema di equazioni
Entrambe le opzioni controllano i metodi utilizzati per risolvere il sistema di equazioni. Per evitare malintesi: Anche quando il sistema di equazioni è risolto direttamente, viene eseguito un calcolo iterativo se ci sono non linearità o se i calcoli sono eseguiti secondo il secondo ordine o analisi di grandi deformazioni. 'Diretto' e 'Iterativo' si riferiscono alla gestione dei dati durante il calcolo.
Quale metodo del risolutore di matrici porta più rapidamente ai risultati dipende dalla complessità del modello e dalle dimensioni della memoria principale (RAM) disponibile. Per i sistemi di piccole e medie dimensioni, il metodo diretto è più efficiente.
Per sistemi molto grandi e complessi, il metodo iterativo porta a risultati più rapidamente.
Teoria della piegatura di lamiere
Le superfici possono essere calcolate secondo le teorie di flessione 'Mindlin' o 'Kirchhoff'. Nel calcolo secondo Mindlin, sono incluse le deformazioni delle forze di taglio; secondo Kirchhoff, non sono presi in considerazione. L'opzione di calcolo Mindlin è quindi adatta per piastre e gusci relativamente spessi utilizzati nelle costruzioni solide, mentre l'opzione Kirchhoff è consigliata per superfici relativamente sottili, come le lamiere nelle costruzioni in acciaio.
Impostazioni del metodo iterativo
Le caselle di controllo in questa sezione di dialogo sono importanti per l'analisi 'Secondo ordine (P-Δ)'.
Riferisci le forze interne alla struttura deformata
Le forze interne e i momenti delle aste sono generalmente visualizzati in relazione alla posizione modificata dei sistemi di coordinate delle aste che si verificano nel sistema deformato. Se si desidera che l'output si riferisca al sistema iniziale non deformato, è possibile definire le forze interne dell'asta e i momenti rilevanti disattivando le caselle di controllo corrispondenti.
Percentuale di iterazioni del metodo di Newton-Raphson in combinazione con Picard
Il metodo secondo Picard si basa su irrigidimenti secanti, mentre il metodo di Newton-Raphson si basa su irrigidimenti tangenti. Quando è selezionata l'opzione di calcolo Newton-Raphson combinata con Picard, gli irrigidimenti secanti vengono utilizzati nelle prime iterazioni prima che gli irrigidimenti tangenti vengano applicati per le restanti iterazioni. Il rapporto tra le prime iterazioni con irrigidimenti secanti è correlato al numero totale di iterazioni.
Conversione della massa in carico
I carichi possono essere definiti non solo come forze e momenti, ma anche sotto forma di masse. Tuttavia, le masse non hanno alcun effetto nell'analisi strutturale. Se vuoi considerarli, seleziona la casella di controllo 'Massa attiva'. Quindi, inserisci il 'Fattore in direzione' per descrivere l'effetto della massa. Pertanto, le masse vengono convertite in forze prima dell'inizio del calcolo e sono incluse nella determinazione delle forze e dei momenti interni.
Utilizzare il pulsante
![]() per passare dall'immissione del coefficiente di massa all'immissione diretta dell'accelerazione. Il nome dei campi di input viene modificato di conseguenza.
per passare dall'immissione del coefficiente di massa all'immissione diretta dell'accelerazione. Il nome dei campi di input viene modificato di conseguenza.
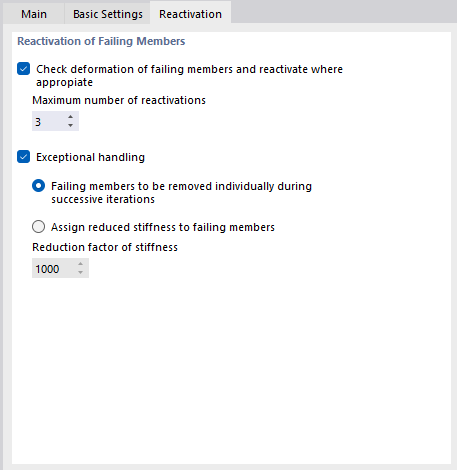
Riattivazione
La scheda Riattivazione è disponibile non appena nel modello è presente un'asta con proprietà non lineari. In questa scheda, è possibile controllare il modo in cui le aste soggette a rottura vengono trattate nell'analisi.
Le aste in rottura sono spesso la causa di problemi di instabilità, ad esempio, quando un modello di asta è irrigidito da aste tese. A causa delle contrazioni delle colonne del telaio dovute al carico verticale, le aste di trazione ricevono piccole forze di compressione nella prima fase di calcolo. Essi saranno rimossi dal sistema. Nella seconda fase, il modello diventa instabile senza queste aste tese. Con le opzioni nella sezione di dialogo 'Riattivazione delle aste in errore', puoi provare a ottenere un calcolo senza messaggi di errore.
Verifica lo spostamento generalizzato di aste che giungono a rottura e riattiva dove é necessario
RFEM analizza gli spostamenti nodali in ogni iterazione. Ad esempio, se le estremità dell'asta di un'asta tesa guasta si allontanano l'una dall'altra, l'asta viene nuovamente utilizzata nella matrice di rigidezza.
La riattivazione delle aste può essere problematica in alcuni casi: Un'asta viene rimossa dopo la prima iterazione, riattivata dopo la seconda, rimossa di nuovo dopo la terza iterazione e così via. Il calcolo eseguirà questo ciclo fino a raggiungere il numero massimo possibile di iterazioni, senza convergere. Il 'Numero massimo di riattivazioni' impedisce questo effetto. È possibile definire la frequenza con cui un elemento dell'asta può essere reinserito prima che venga finalmente rimosso dalla matrice di rigidezza.
Trattamento eccezionale
Se si seleziona la casella di controllo 'Gestione eccezionale', è possibile selezionare tra due metodi per gestire le aste in errore. Possono essere combinati con la riattivazione sopra descritta.
- Aste che giungono a rottura da rimuovere individualmente durante le iterazioni successive
Dopo la prima iterazione, RFEM non rimuove, ad esempio, tutte le aste tese con una forza di compressione in una volta, ma solo l'asta tesa con la forza di compressione maggiore. Nella seconda iterazione, nella matrice di rigidezza manca una sola asta. Successivamente, l'asta di trazione con la forza di compressione maggiore viene nuovamente rimossa. In questo modo, il sistema mostra spesso un migliore comportamento di convergenza a causa degli effetti di ridistribuzione.
Questa opzione di calcolo richiede più tempo perché il programma deve eseguire un maggior numero di iterazioni. Inoltre, è necessario assicurarsi che nella scheda 'Principale' sia fornito un sufficiente Numero massimo di iterazioni.
- Assegna una rigidezza ridotta alleaste che giungono a rottura
Le aste che giungono a rottura non vengono rimosse dalla matrice di rigidezza, ma viene invece assegnata una rigidezza molto piccola. Puoi definirlo nel campo 'Coefficiente di riduzione della rigidezza': Un coefficiente di 1000 significa che la rigidezza dell'asta è ridotta a 1/1000.
Precisione e tolleranza
La scheda Precisione e tolleranza consente di influenzare i parametri di convergenza e tolleranza del calcolo. Tuttavia, è necessario modificare le impostazioni predefinite solo in casi eccezionali.
Precisione del criterio di convergenza del calcolo non-lineare
Se agiscono effetti non lineari o se del secondo ordine o viene eseguita un'analisi di grandi deformazioni, il calcolo può essere influenzato mediante criteri di convergenza.
Il cambiamento delle forze assiali delle ultime due iterazioni è messo a confronto asta per asta. Non appena la modifica raggiunge il valore di un numero frazionale specifico della forza massima assiale, il calcolo si arresta. Tuttavia, durante le iterazioni può accadere che le forze assiali oscillino tra due valori. È possibile prevenire questo effetto pendolo regolando la "sensibilità".
La precisione influenza anche il criterio di convergenza per le variazioni di deformazione nei calcoli eseguiti secondo l'analisi di grandi deformazioni, dove sono considerate le non linearità geometriche. Il valore predefinito è 1,00. Il coefficiente minimo è 0,01, il valore massimo 100,00. Minore è il valore, più vicino deve essere il termine di convergenza al termine di confronto. La precisione del risultato è aumentata di conseguenza.
Tolleranza per il rilevamento dell'instabilità
Esistono diversi approcci per analizzare il comportamento di stabilità di un modello. Tuttavia, nessuno di questi è in grado di rilevare matrici di rigidezza singolari con assoluta affidabilità.
RFEM utilizza due procedure per determinare le instabilità: Da un lato, gli elementi sulla diagonale principale della matrice di rigidezza sono sempre confrontati assolutamente con lo stesso numero nelle iterazioni. D'altra parte, ogni elemento della diagonale principale viene analizzato rispetto al numero adiacente. La tolleranza può essere modificata nel campo. Minore è il valore della tolleranza, più il limite di instabilità del modello' si avvicina all'esatta posizione di instabilità. La precisione del risultato è aumentata di conseguenza.
Impostazione relativa del time step per il rilassamento dinamico
Il parametro time controlla il calcolo secondo il metodo di dinamico-rilassamento dinamico. Minore è il valore, minore è l'intervallo di tempo entro il quale vengono registrate tutte le fluttuazioni della risposta. L'accuratezza dei risultati è aumentata di conseguenza.
Robustezza del calcolo iterativo
Nel caso di problemi di convergenza con il metodo di Newton-Raphson, la robustezza può essere rafforzata per evitare che la soluzione "salta". Riducendo il valore, il numero di soluzioni possibili viene ridotto in caso di presenza di un ramo di soluzione orizzontale non convergente, e quindi anche la possibilità di un risultato valido all'interno delle iterazioni specificate. Potrebbe essere necessario aumentare il numero massimo di iterazioni.