Ustawienie analizy statycznej ( SA ) określa zasady, według których obliczane są przypadki obciążeń i kombinacje obciążeń. Wstępnie ustawione są trzy standardowe typy analizy.
Łącznie
W zakładce Główne można zarządzać ustawieniami dla analizy statyczno-wytrzymałościowej i podstawowych parametrów obliczeń.
Typ analizy
W tej sekcji okna dialogowego można określić teorię obliczeń, zgodnie z którą analizowane są przypadki obciążeń i kombinacje obciążeń. Z listy 'Typ analizy' można wybrać trzy podejścia.
Geometrycznie liniowa
Podczas obliczeń zgodnie z analizą geometrycznie liniową (pierwszego rzędu) równowaga jest analizowana na niezdeformowanym układzie konstrukcyjnym. Analiza liniowa jest przeprowadzana, ponieważ odkształcenia elementów nie są uwzględniane w obliczeniach.
Przypadki obciążeń są domyślnie obliczane zgodnie z analizą geometrycznie liniową.
Drugi rząd (P-Δ)
W analizie „konstrukcyjnej” drugiego rzędu równowaga jest określana na zdeformowanym układzie konstrukcyjnym. Przyjmuje się przy tym, że deformacje są niewielkie. Siły osiowe w układzie mają wpływ na wzrost momentów zginających. Dlatego analiza ta jest stosowana, gdy siły osiowe są znacznie większe niż siły tnące.
Kombinacje obciążeń są domyślnie obliczane nieliniowo zgodnie z analizą drugiego rzędu.
Duże deformacje
Analiza dużych deformacji (trzeciego rzędu lub teoria dużych deformacji) uwzględnia w obliczeniach siły podłużne i poprzeczne. Po każdym kroku iteracji tworzona jest macierz sztywności odkształconego układu. Obciążenia są obsługiwane w sposób zróżnicowany: Obciążenie zdefiniowane w kierunku globalnym zachowuje swój kierunek w przypadku skręcenia elementów skończonych. Jeżeli obciążenie działa w kierunku lokalnego pręta lub osi powierzchni, zmienia swój kierunek zgodnie z skręceniem elementu.
Jeżeli model zawiera pręty kablowe, obliczenia według analizy dużych deformacji są wstępnie ustawione.
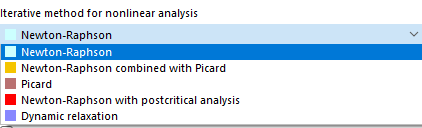
Metoda iteracyjna dla analizy nieliniowej
W zależności od typu analizy dostępne są różne metody rozwiązywania nieliniowego układu równań.
Newton-Raphson
Metoda Newtona-Raphsona jest domyślnie ustawiona w przypadku analizy dużych deformacji. Nieliniowy układ równań rozwiązywany jest numerycznie metodą iteracyjnych przybliżeń przy użyciu stycznych. Styczna macierz sztywności jest określana jako funkcja aktualnego stanu odkształcenia; jest ona odwracana w każdym cyklu iteracji. Metoda ta w większości przypadków pozwala uzyskać szybką zbieżność (kwadratową).
Metoda Newtona-Raphsona połączona z metodą Picarda
Podejście według Picard jest stosowane jako pierwsze. Po kilku iteracjach następuje przełączenie na metodę Newton-Raphson. Podstawową ideą tego podejścia jest zastosowanie stosunkowo „niewrażliwej” metody Picarda w pierwszych krokach iteracji w celu uniknięcia komunikatów o niestabilności. To początkowe przybliżenie zostaje następnie zastąpione przez szybką metodę Newtona-Raphsona w celu znalezienia ostatecznego stanu równowagi.
Metoda Picarda
Metodę według Picarda, zwaną również metodą siecznych, można rozumieć jako przybliżenie skończonej różnicy metody Newton-Raphson. Program uwzględnia różnicę pomiędzy bieżącym a pierwotnym cyklem iteracji w aktualnym kroku przyrostu obciążenia. Metoda ta jest z reguły wolniej zbieżna niż metoda obliczeniowa według Newtona-Raphsona. Jednak okazuje się również, że jest mniej wrażliwy na problemy nieliniowe, co sprawia, że obliczenia są bardziej stabilne.
Metoda Newtona-Raphsona z analizą postkrytyczną
Metoda ta jest przydatna w przypadku rozwiązywania problemów pokrytycznych, w przypadku których należy przezwyciężyć szereg niestabilności. Jeżeli występuje niestateczność, a macierz sztywności nie może zostać odwrócona, program wykorzystuje macierz sztywności z ostatniego stabilnego kroku iteracji. Program kontynuuje obliczenia przy użyciu tej macierzy do momentu ponownego osiągnięcia zakresu stateczności.
Relaksacja dynamiczna
Ostatnia metoda przeznaczona jest do obliczeń według analizy dużych deformacji oraz do analizy postkrytycznej. W przypadku zastosowania tego podejścia zostaje wprowadzony sztuczny parametr czasu. Przy uwzględnieniu bezwładności i tłumienia uszkodzenie można rozpatrywać jako problem dynamiczny. Podejście to wykorzystuje jawną metodę integracji czasowej. Macierz sztywności nie jest przy tym odwracana. W przypadku obliczeń metodą relaksacji dynamicznej żadna część modelu nie może mieć ciężaru właściwego równego zero.
Metoda ta obejmuje również tłumienie Rayleigha, które można zdefiniować za pomocą stałych α i β zgodnie z poniższym równaniem z pochodnymi czasowymi:
|
M |
Skupiona (ukośna) macierz mas |
|
C |
Ukośna macierz tłumienia C = α M + βdiag[K11 ( u ),K22 ( u ),...,Knn ( u )] |
|
K |
Macierz sztywności |
|
f |
Wektor sił zewnętrznych |
|
u |
Dyskretyzowany wektor przemieszczenia |
Elementy sterujące dla analizy nieliniowej
'Maksymalna liczba iteracji' określa, ile przebiegów obliczeniowych zostanie wykonanych maksymalnie dla analizy według drugiego rzędu lub analizy dużych deformacji oraz dla obiektów działających nieliniowo. Gdy obliczenia osiągną granicę bez osiągnięcia stanu równowagi, pojawi się odpowiedni komunikat. Następnie możesz zdecydować, czy chcesz wyświetlić wyniki.
'Liczba przyrostów obciążenia' jest istotna dla obliczeń według drugiego rzędu lub według analizy dużych odkształceń. Podczas uwzględniania dużych deformacji znalezienie równowagi jest często trudne. Niestateczności można uniknąć, przykładając obciążenie w kilku krokach. Na przykład w przypadku określenia dwóch przyrostów obciążenia w pierwszym kroku przyłożona zostanie połowa obciążenia. Iteracje przeprowadzane są do momentu osiągnięcia stanu równowagi. Następnie, w drugim etapie, układ już odkształcony zostaje przyłożony do pełnego obciążenia i powtarzane są iteracje aż do osiągnięcia stanu równowagi.
Opcje I
W tej sekcji okna dialogowego można aktywować różne 'ustawienia specjalne' w celu manipulowania obliczeniami według drugiego rzędu lub według analizy dużych odkształceń.
Zmień domyślne ustawienia dokładności i tolerancji
Po zaznaczeniu pola wyboru 'Modyfikuj standardowe ustawienia dokładności i tolerancji', w oknie dialogowym zostaje dodana zakładka Dokładność i tolerancja. Tam można dostosować kryteria zbieżności.
Ignoruj wszystkie nieliniowości
Za pomocą pola wyboru 'Ignoruj wszystkie nieliniowości' można wyłączyć nieliniowość elementów dla obliczeń. Na przykład pręty rozciągane pozostają w modelu, gdy tylko wystąpią siły ściskające. Właściwości nieliniowe należy jednak wyłączyć tylko w celach testowych; na przykład, aby znaleźć przyczynę niestabilności. Czasami za przerwanie obliczeń odpowiedzialne są błędnie zdefiniowane kryteria uszkodzenia.
Opcje II
Modyfikuj obciążenie za pomocą mnożnika
Po zaznaczeniu tego pola wyboru można zdefiniować współczynnik k, przez który mają zostać pomnożone wszystkie obciążenia.
Starsze normy zawierają wymóg globalnego mnożenia obciążeń przez określony współczynnik w celu zwiększenia efektów według teorii II rzędu dla obliczeń stateczności. Z kolei wymiarowanie konstrukcji należy przeprowadzać z obciążeniami charakterystycznymi. Oba wymagania można spełnić, wprowadzając współczynnik większy niż 1 i aktywując pole wyboru 'Podziel wyniki według współczynnika obciążenia'.
W przypadku analiz zgodnie z obowiązującymi normami nie należy edytować obciążenia za pomocą współczynników. Zamiast tego w przypadku superpozycji w sytuacjach obliczeniowych należy uwzględnić częściowe współczynniki bezpieczeństwa i współczynniki kombinacji.
Uwzględnij korzystne oddziaływanie sił rozciągającychw prętach
Siły rozciągające mają korzystny wpływ na wstępnie odkształcony układ konstrukcyjny. Dzięki temu odkształcenie zostaje zredukowane, a konstrukcja stabilizowana. Zwykle wykorzystujemy ten efekt w obliczeniach według analizy drugiego rzędu i analizy dużych deformacji; na przykład w przypadku hal ze stężeniami lub konstrukcji ogólnych narażonych na zginanie. Odciążenie wywołane oddziaływaniem sił rozciągających dla belek usztywnionych od dołu (belki ze ściągiem lub kablami) może spowodować niepożądane zmniejszenie odkształceń i sił wewnętrznych.
Sprawdzenie stateczności na podstawie prędkości deformacji
Po zaznaczeniu tego pola wyboru program RFEM sprawdza, jak rozwijają się odkształcenia w trakcie iteracji podczas obliczeń. Jeżeli przemieszczenia lub obroty gwałtownie wzrosną i przekroczą wewnętrzną wartość graniczną programu, obliczenia zostaną przerwane i wyświetlony zostanie komunikat o niestabilności.
Spróbuj obliczyć niestateczną konstrukcję
To pole wyboru umożliwia podjęcie próby obliczenia niestatecznego modelu. W pierwszym kroku obliczeń program RFEM stosuje małe sprężyny stabilizujące model w pierwszej iteracji. Po osiągnięciu stateczności początkowej, a przed przeprowadzeniem dalszych iteracji, sprężystości te są usuwane
Przemieszczenia od obciążenia pręta typu 'ciśnienie wewnętrzne rury'
To pole wyboru jest odpowiednie dla obciążenia pręta zwanego ciśnieniem wewnętrznym rury. Tak zwany efekt Bourdona opisuje tendencję wygiętej rurki do prostowania się pod wpływem ciśnienia. Zarówno naprężenia obwodowe, jak i osiowe wywołane ciśnieniem wewnętrznym prowadzą do odkształcenia podłużnego rury, biorąc pod uwagę sztywność materiału i odkształcenie poprzeczne.
W tym artykule https://www.dlubal.com/en-US/support-and-learning/support/knowledge-base/001102 można zapoznać się z przykładem sposobu obliczania ciśnienia wewnętrznego rur.
Zapisz wyniki wszystkich przyrostów obciążenia
Jeżeli obciążenie jest przykładane przyrostowo (patrz Kontrolki dla analizy nieliniowej), można użyć tego pola wyboru, aby wymusić wyprowadzenie wyników pośrednich w celu sprawdzenia wyników poszczególnych przyrostów obciążenia.
Niesymetryczny solwer bezpośredni
Niesymetryczny solwer równań bezpośrednich jest używany dla nieliniowego modelu materiału (patrz rozdział Nieliniowe zachowanie materiału) z asymetrycznymi właściwościami dla rozciągania i ściskania. To pole wyboru umożliwia użycie tego solwera równań również w przypadku innych modeli materiałowych, takich jak model materiałowy izotropowo nieliniowo sprężysty.
Równowaga dla konstrukcji nieodkształconej
To pole wyboru umożliwia analizę konstrukcji nieodkształcającej się, czyli układu konstrukcyjnego, którego odkształcenia pozostają zerowe. Ta opcja analizy może być przydatna, gdy układ jest obciążony, na przykład z powodu przypadku obciążenia, a powstałe odkształcenia można uznać za zanikające.
Jednym z obszarów zastosowania do obliczania równowagi dla konstrukcji niezdeformowanej jest pierwotny stan naprężeń w analizie geotechnicznej. W ramach przypadku lub kombinacji obciążeń należy określić działające naprężenia wynikające z obciążenia wstępnego gruntem. Odkształcenia takiego przypadku obciążenia lub kombinacji nie są jednak przedmiotem zainteresowania i dlatego nie mogą być dalej wykorzystywane.
Ustawienia podstawowe
Zakładka Ustawienia podstawowe umożliwia zarządzanie podstawowymi specyfikacjami dla obliczeń.
Stosunek obciążeń stałych
Pole wyboru 'Określ dla kombinacji obciążeń' umożliwia określenie stopnia obciążenia działającego trwale w kombinacji obciążeń. Wybierz kombinację obciążeń z listy lub utwórz nową za pomocą przycisku
![]() . Następnie na liście 'Porównaj wartość wyników' można zdefiniować stosunki, które mają wpływ statyczny lub zmienny.
. Następnie na liście 'Porównaj wartość wyników' można zdefiniować stosunki, które mają wpływ statyczny lub zmienny.
Współczynnik obciążenia stałego można uznać za zgodny z normami w obliczeniach.
Metoda układu równań
Obie opcje sterują metodami rozwiązywania układu równań. Należy przy tym pamiętać, że Nawet jeśli układ równań jest rozwiązywany bezpośrednio, obliczenie iteracyjne jest przeprowadzane, jeśli występują nieliniowości lub jeśli obliczenia są przeprowadzane zgodnie z zasadą drugiego rzędu lub według analizy dużych odkształceń. Parametry 'Direct' i 'Iterative' odnoszą się do zarządzania danymi podczas obliczeń.
To, która metoda solwera macierzy szybciej prowadzi do wyników, zależy od złożoności modelu oraz od rozmiaru dostępnej pamięci operacyjnej (RAM). W przypadku małych i średnich systemów bardziej efektywna jest metoda bezpośrednia .
W przypadku bardzo dużych układów metoda iteracyjna prowadzi do uzyskania wyników szybciej.
Teoria zginania płyt
Powierzchnie mogą być obliczane zgodnie z teoriami zginania 'Mindlin' lub 'Kirchhoff'. W obliczeniach według Mindlina uwzględniane są odkształcenia od sił tnących, natomiast w obliczeniach według Kirchhoffa są one pomijane. Opcja obliczeń Mindlin jest zatem odpowiednia dla stosunkowo grubych płyt i powłok stosowanych w konstrukcjach bryłowych, natomiast opcja Kirchhoff jest zalecana dla powierzchni, które są stosunkowo cienkie, takich jak blachy w konstrukcjach stalowych.
Ustawienia metody iteracyjnej
Pola wyboru w tej sekcji okna dialogowego są ważne dla analizy 'Drugiego rzędu (P-Δ)'.
Odnieś siły wewnętrzne do odkształconej konstrukcji
Siły wewnętrzne i momenty prętów są zwykle wyświetlane w odniesieniu do zmienionego położenia układów współrzędnych pręta powstających w odkształconym układzie. Jeżeli wyniki mają odnosić się do niezdeformowanego układu początkowego, można zdefiniować odpowiednie siły wewnętrzne i momenty pręta, wyłączając odpowiednie pola wyboru.
Procentowy udział iteracji dla metody Newtona-Raphsona połączonej z metodą Picarda
Metoda według Picarda opiera się na usztywnieniach siecznych, natomiast metoda Newtona-Raphsona na usztywnieniach stycznych. W przypadku wybrania opcji obliczeń Newton-Raphson w połączeniu z Picard sieczne usztywnienia są używane w pierwszych iteracjach przed zastosowaniem usztywnień stycznych dla pozostałych. Stosunek liczby pierwszych iteracji z usztywnieniami siecznymi jest powiązany z całkowitą liczbą iteracji.
Konwersja masy na obciążenie
Obciążenia mogą być definiowane nie tylko jako siły i momenty, ale również w postaci mas. Jednak masy nie mają wpływu na analizę statyczno-wytrzymałościową. Aby je uwzględnić, należy zaznaczyć pole wyboru 'Masa czynna'. Następnie należy wprowadzić 'Współczynnik w kierunku' opisujący wpływ masy. W ten sposób masy są przekształcane w siły przed rozpoczęciem obliczeń i są uwzględniane przy określaniu sił wewnętrznych i momentów.
Za pomocą przycisku
![]() można przełączać się między wprowadzaniem współczynnika masy a bezpośrednim wprowadzaniem przyspieszenia. Nazwy pól wprowadzania są odpowiednio dostosowywane.
można przełączać się między wprowadzaniem współczynnika masy a bezpośrednim wprowadzaniem przyspieszenia. Nazwy pól wprowadzania są odpowiednio dostosowywane.
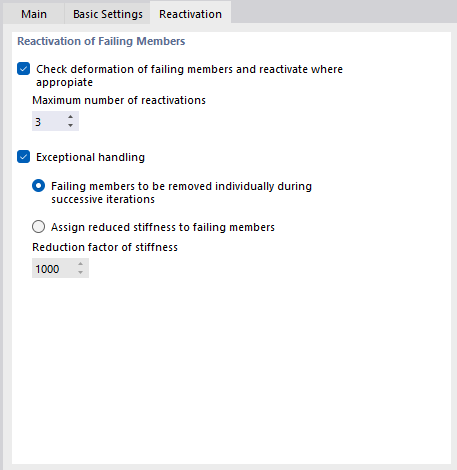
Reaktywacja
Zakładka Reaktywacja jest dostępna, gdy w modelu pojawi się pręt o właściwościach nieliniowych. Na tej karcie można określić sposób traktowania ulegających uszkodzeniu prętów w analizie.
Uszkodzone pręty są często przyczyną problemów z niestatecznością, na przykład, gdy model prętowy jest usztywniony prętami rozciąganymi. Ze względu na skrócenie słupa ramy pod wpływem obciążenia pionowego, w pierwszym kroku obliczeń na pręty rozciągane są niewielkie siły ściskające. i usuwane z układu. W drugim kroku model staje się niestabilny bez tych prętów rozciąganych. Za pomocą opcji w sekcji 'Ponowna aktywacja prętów ulegających uszkodzeniu' można spróbować przeprowadzić obliczenia bez komunikatu o błędzie.
Kontrola deformacji i ewentualna reaktywacja uszkodzonych prętów
Program RFEM analizuje przemieszczenia węzłowe w każdej iteracji. Na przykład, jeżeli końce uszkodzonego pręta rozciąganego oddalą się od siebie, pręt zostanie ponownie użyty w macierzy sztywności.
Ponowna aktywacja prętów może być w niektórych przypadkach problematyczna: Pręt jest usuwany po pierwszej iteracji, reaktywowany po drugiej, ponownie usuwany po trzeciej iteracji itd. W ramach obliczeń ta pętla byłaby prowadzona bez zbieżności do momentu osiągnięcia maksymalnej możliwej liczby iteracji. 'Maksymalna liczba reaktywacji' zapobiega temu efektowi. Można zdefiniować, jak często element prętowy może być ponownie wstawiony, zanim zostanie ostatecznie usunięty z macierzy sztywności.
Postępowanie wyjątkowe
W przypadku zaznaczenia pola wyboru 'Wyjątkowa obsługa' można wybrać jedną z dwóch metod postępowania z prętami ulegającymi uszkodzeniu. Można je łączyć z reaktywacją opisaną powyżej.
- Usuwanie uszkodzonych prętów pojedynczo w kolejnych iteracjach
Po pierwszej iteracji program RFEM nie usuwa od razu wszystkich prętów rozciąganych, w których występuje siła ściskająca, a jedynie pręt rozciągany, w którym występuje największa siła ściskająca. W ten sposób w drugiej iteracji w macierzy sztywności brakuje tylko jednego pręta. W kolejnym kroku program RFEM ponownie usuwa pręt rozciągany, w którym występuje największa siła ściskająca. W ten sposób układ często wykazuje lepszą zbieżność ze względu na efekty redystrybucji.
Ten wariant obliczeń wymaga więcej czasu ze względu na to, że program musi wykonać większą liczbę iteracji. Ponadto należy upewnić się, że w zakładce 'Główne' podano wystarczającą Maksymalna liczba iteracji.
- Przypisz uszkodzonym prętom zredukowaną sztywność
Po zaznaczeniu tej opcji uszkodzone pręty nie są usuwane z macierzy sztywności, lecz przydzielana im jest bardzo mała sztywność. Wartość tę można zdefiniować w polu 'Współczynnik redukcyjny sztywności': Współczynnik 1000 oznacza, że sztywność pręta jest zmniejszona do 1/1000.
Dokładność i tolerancja
Zakładka Dokładność i tolerancja umożliwia wpływanie na parametry zbieżności i tolerancji obliczeń. Ustawienia domyślne należy zmieniać tylko w wyjątkowych przypadkach.
Dokładność kryterium zbieżności dla obliczeń nieliniowych
Jeżeli działają efekty nieliniowe lub jeżeli efekty są drugorzędne lub po przeprowadzeniu analizy dużych deformacji, na obliczenia można wpłynąć za pomocą kryteriów zbieżności.
Zmiana sił osiowych dwóch ostatnich iteracji jest porównywana w poszczególnych prętach. Gdy zmiana ta osiągnie określony ułamek maksymalnej siły osiowej, obliczenia zostaną zakończone. Podczas iteracji może się jednak zdarzyć, że siły osiowe oscylują między dwiema wartościami. Efektowi wahadła można zapobiec, dostosowując „czułość”.
Dokładność wpływa również na kryterium zbieżności dla zmian odkształceń podczas obliczeń według analizy dużych deformacji, w których uwzględniane są nieliniowości geometryczne. Wartość domyślna to 1,00. Współczynnik minimalny wynosi 0,01, a maksymalna 100,00. Im mniejsza wartość, tym składnik zbieżności musi być bliższy składnikowi porównania. Odpowiednio zwiększa się dokładność wyników.
Tolerancja dla wykrywania niestateczności
Istnieją różne podejścia do analizy zachowania stateczności modelu. Żadne z nich nie gwarantuje jednak z całkowitą pewnością wykrycia osobliwych macierzy sztywności.
Program RFEM wykorzystuje dwie procedury do wykrywania niestateczności: Z jednej strony, elementy na głównej przekątnej macierzy sztywności są zawsze porównywane bezwzględnie z tą samą liczbą w iteracjach. Z drugiej strony, każdy element głównej przekątnej jest analizowany względem sąsiedniego numeru. Tolerancję można ustawić w polu wprowadzania. Im mniejsza wartość tolerancji, tym bliżej granica niestateczności modelu' jest przesuwana do dokładnego miejsca niestabilności. Odpowiednio zwiększa się dokładność wyników.
Względne ustawienie kroku czasowego dla relaksacji dynamicznej
Parametr czasu steruje obliczeniami zgodnie z metodą dynamiczna relaksacja. Im mniejsza wartość, tym mniejszy krok czasowy, w którym rejestrowane są wszystkie fluktuacje odpowiedzi. Odpowiednio zwiększa się dokładność wyników.
Stabilność obliczeń iteracyjnych
W przypadku problemów ze zbieżnością metody Newtona-Raphsona, odporność można wzmocnić, aby zapobiec „przeskakiwaniu” rozwiązania. Zmniejszając wartość, zmniejsza się liczba możliwych rozwiązań w przypadku obecności niezbieżnej poziomej gałęzi rozwiązania, a tym samym zmniejsza się również możliwość uzyskania prawidłowego wyniku w określonych iteracjach. Może to wymagać zwiększenia maksymalnej liczby iteracji.