Elementy skończone w programie RFEM

Elementy 1D

W przypadku elementów prętowych przyjmuje się, że przekrój po odkształceniu pozostaje płaski. "Elementy 1D" wykorzystywane są do modelowania belek, kratownic, żeber, kabli oraz połączeń sztywnych. Element prętowy 1D ma łącznie dwanaście stopni swobody - sześć na początku i sześć na końcu elementu, dla przemieszczeń (u_x, u_y, u_z) i obrotów (φ_x, φ_y, φ_z). Podczas obliczeń liniowych rozciąganie, ściskanie i skręcanie są wyrażone jako liniowe funkcje osi x pręta, niezależnie od zginania i siły tnącej. Funkcje te są aproksymowane wielomianem 3 rzędu w x, z uwzględnieniem wpływu naprężeń ścinających od sił poprzecznych V_y i V_z. Macierz sztywności K_L (12, 12) opisuje liniowe zachowanie elementów 1D. Wzajemne oddziaływanie siły osiowej i zginania w przypadku problemów geometrycznie nieliniowych jest wyrażone macierzą sztywności K_NL (12, 12). Więcej informacji można znaleźć w [1] i [2].

Do obliczeń według analizy dużych deformacji zaleca się stosowanie zagęszczenia siatki linii, pozwalającego na dokładne obliczenie wyników.

Elementy 2D

W przypadku powierzchni tworzone są elementy 2D. Wszędzie tam, gdzie nie można zastosować elementów czworokątnych, generator siatki wstawia elementy trójkątne.

Stopnie swobody elementów czworokątnych i trójkątnych w węzłach są takie same, jak w przypadku elementów 1D: stopnie swobody przemieszczenia (u_x, u_y, u_z) i obrotu (φ_x, φ_y, φ_z ). Zapewnia to kompatybilność elementów 1D i 2D w węzłach. Parametry są zdefiniowane w płaskim lokalnym układzie współrzędnych elementu, a podczas tworzenia globalnej macierzy sztywności przeliczane są na globalny układ współrzędnych.

Elementy czworokątne dla powłok w RFEM

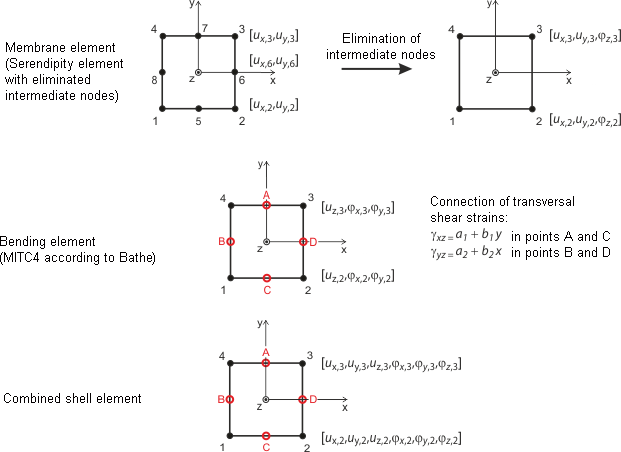
Rysunek Elementy czworokątne dla powłok przedstawia podejście do płaskich elementów powłokowych, opierające się na teorii Mindlina/Reissnera. Aby zapewnić bezpośrednie połączenie z elementami prętowymi, przyjmuje się podejście kwadratowe w płaszczyźnie powłoki (u_x, u_y). Poprzez wyeliminowanie węzłów pośrednich powstaje element czterowęzłowy z dodatkowymi stopniami swobody obrotu w kierunku x, y i z. Umożliwia to bezpośrednie połączenie z elementami belkowymi w przypadku elementów powłokowych. W oparciu o interpolację mieszaną przemieszczeń poprzecznych, obrotów przekroju i poprzecznych odkształceń od ścinania, stosuje się wprowadzone przez Bathe'a i Dvorkina [3] elementy MITC (Mixed Interpolation of Tensorial Components): MITC3+ dla trójkątów, MITC4 dla czworokątów.

Elementy prętowe są obecnie uwzględniane przez bezpośrednie rozwiązanie równania różniczkowego według teorii drugiego rzędu. Uwzględnienie efektów skręcania skrępowanego przy zastosowaniu modelu skręcania Saint Venanta nie jest możliwe.

Obliczenia membranowe oparte są na zasadach Bergana [4] [5] [6]. Funkcje podstawowe są podzielone, np. w przypadku elementów trójkątnych na trzy deformacje ciała sztywnego, trzy stałe stany odkształcenia oraz trzy specjalne liniowe rozkłady naprężeń i odkształceń. Pole odkształceń wewnątrz elementu jest kwadratowe, a pole naprężeń – liniowe. Macierz sztywności elementu K_L K_L jest następnie przekształcana na dziewięć wspólnych parametrów typów u_x, u_y, φ_z. Składowe tej macierzy są wstawiane do całkowitej macierzy sztywności (18, 18), wraz ze składowymi powodującymi zginanie i ścinanie. Macierz ta jest wynikiem koncepcji Lynna/Dhillona. Zostają przy tym zastosowane tak zwane płyty Mindlina (płyty z wyraźnym odkształceniem od ścinania), które są obliczane w oparciu o teorię Timoschenki. W ten sposób program RFEM znajduje prawidłowe rozwiązanie zarówno dla grubych, jak i cienkich płyt (płyt Naviera).

W przypadku nieliniowych problemów geometrycznych nie jest możliwe rozłożenie stanu naprężeń-odkształceń na stan płaski i na zginanie/ścinanie w sposób opisany powyżej. Wzajemny wpływ tych stanów jest uwzględniony w macierzy K_NL. Program RFEM wykorzystuje dość prostą, ale efektywną postać macierzy K_NL, opartą na metodach Zienkiewicza [7]. Stosowana jest kwadratowa składowa ε₂ tensora odkształceń Greena/Lagrange'a ε = ε₁ + ε₂. Zakłada się przy tym liniowy rozkład u_z(x, y) płaskiego stanu naprężeń oraz liniowe rozkłady u_x(x, y) i u_y(x, y) przy interakcji ze zginaniem. Założenie to jest możliwe ze względu na to, że główny efekt interakcji zależy od pierwszej pochodnej równania różniczkowego, a wpływ składowych wyższego rzędu maleje bardzo szybko wraz z podziałem na mniejsze elementy. Poprawność tej procedury potwierdzają analizy numeryczne.

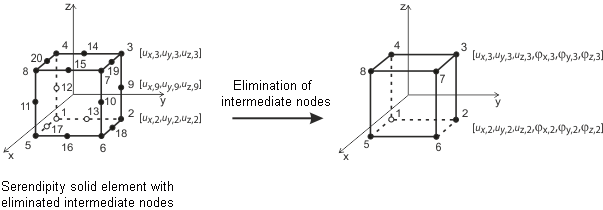
Elementy 3D

Elementy 3D są stosowane dla brył. W programie RFEM zaimplementowane są następujące typy elementów: czworościan, pięciościan (graniastosłup, ostrosłup) i sześcian. Niniejsza instrukcja nie zawiera szczegółowego opisu stosowanych elementów i macierzy. Szczegółowe informacje można znaleźć w: Sevcik, 3D Finite Elements with Rotational Degrees of Freedom [8]. Dokument ten jest udostępniany na życzenie przez firmę Dlubal Software.

Element bryłowy (sześcian)

W przypadku brył wszystkie stopnie swobody obrotu należy sklasyfikować jako krytyczne. Ze względu na to, że odkształcenie bryły jest określane wyłącznie na podstawie wektorów przemieszczenia, obrót węzła siatki (np. wskutek przyłożenia momentu skręcającego) nie wpływa na odkształcenie w bryle.