Elementi finiti in RFEM

Elementi 1D

Per gli elementi dell'asta, si presume che la sezione trasversale rimanga piana durante la deformazione. Gli "elementi 1D" sono utilizzati per rappresentare travi, travature reticolari, nervature, funi e giunti rigidi. Un elemento dell'asta 1D ha un totale di dodici gradi di libertà - sei all'inizio e sei alla fine dell'elemento, ciascuno per gli spostamenti (_ux, u_y, u_z ) e rotazioni (φ_x, φ_y, φ_z ). Quando si calcolano i dati strutturali linearmente, trazione, compressione e torsione sono espresse come funzioni lineari dell'asse x dell'asta, indipendentemente dalla flessione e dal taglio. Queste funzioni sono approssimate da un polinomio del terzo ordine in x, inclusa l'influenza delle tensioni tangenziali dalle forze di taglio V_y e V_z. La matrice di rigidezza K_L (12, 12) descrive il comportamento lineare degli elementi 1D. L'interazione reciproca tra forza assiale e flessione in caso di problemi geometricamente non lineari è espressa nella matrice di rigidezza K_NL (12, 12). Per ulteriori informazioni, vedere [1] e [2].

Per i calcoli secondo l'analisi a grandi spostamenti, si consiglia di utilizzare un Infittimento della mesh della linea in modo che i risultati dell'asta possano essere determinati con la precisione corrispondente.

Elementi 2D

Per le superfici, vengono creati elementi 2D. Laddove non è possibile utilizzare elementi quadrangolari, il generatore di mesh inserisce elementi triangolari.

I gradi di libertà degli elementi quadrangolari e triangolari nei nodi d'angolo sono gli stessi degli elementi 1D: gradi di libertà di spostamento (u_x, u_y, u_z ) e di rotazione (φ_x, φ_y, φ_z ). Ciò garantisce la compatibilità tra gli elementi 1D e 2D nei nodi. I parametri sono definiti nel sistema di coordinate locali planari degli elementi e sono convertiti nel sistema di coordinate globali quando si compone la matrice di rigidezza globale.

Elementi quadrangolari per gusci in RFEM

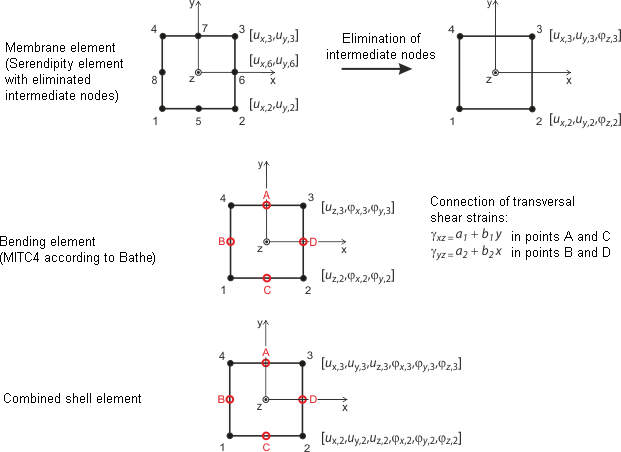
L'immagine Elementi quadrangolari per gusci mostra l'approccio per elementi gusci piani. Si basa sulla teoria di Mindlin/Reissner. Per garantire l'accoppiamento diretto con gli elementi dell'asta, viene scelto un approccio quadrato nel piano del guscio (_ux, u_y ). Eliminando i nodi intermedi, viene creato un elemento a quattro nodi con gradi di libertà rotazionali aggiuntivi nelle direzioni x, y e z. Pertanto, per gli elementi a diaframma è possibile un accoppiamento diretto con elementi a trave. Basato su un'interpolazione combinata di spostamenti trasversali, rotazioni della sezione trasversale e deformazioni tangenziali trasversali, i metodi di Bathe e Dvorkin elementi MITC presentati da efer [3] ( Mixed Interpolation of Tensorial Components ) sono stati utilizzati: MITC3+ per triangoli, MITC4 per quadrangoli.

Al momento, gli elementi asta sono considerati risolvendo direttamente l'equazione differenziale secondo l'analisi del secondo ordine. Gli effetti di ingobbamento non possono essere considerati quando si utilizza la torsione di Saint Venant.

I calcoli delle membrane si basano sui principi di Bergan [4] [5] [6]. Per gli elementi triangolari, ad esempio, le funzioni di base sono divise in tre deformazioni del corpo rigido, tre condizioni di deformazione costante e tre speciali gradienti lineari di tensione e deformazione. Il campo di deformazione all'interno di un elemento è quadratico e il campo di tensione è lineare. La matrice di rigidezza dell'elemento K_L è successivamente trasformata in nove parametri collettivi dei tipi u_x, u_y, φ_z. I componenti di questa matrice sono inseriti insieme ai componenti per flessione e taglio nella matrice di rigidezza complessiva (18, 18). Questa matrice è il risultato del concetto di Lynn/Dhillon. In questo modo, vengono applicate le cosiddette piastre Mindlin (piastre con deformazione a taglio distinta) e analizzate secondo Timoshenko. In questo modo, RFEM trova la soluzione corretta sia per le piastre spesse che per quelle sottili (piastre di Navier).

Nel caso di problemi geometricamente non lineari, la suddetta divisione della condizione tensione-deformazione in uno stato planare e in flessione/taglio non è possibile. Le influenze reciproche di questi stati sono considerate nella matrice K_NL. RFEM utilizza una forma piuttosto semplice ma efficace della matrice K_NL che si basa sugli approcci di Zienkiewicz [7]. Viene applicata la componente quadrata ε₂ del tensore di deformazione di Green/Lagrange ε = ε₁ + ε₂. Si assume una distribuzione lineare di u_z (x, y) della condizione di tensione planare e distribuzioni lineari di u_x (x, y) e u_y (x, y) dell'interazione con la flessione. Questa ipotesi è possibile, perché l'effetto principale dell'interazione dipende dalla prima derivazione dell'equazione differenziale e perché l'influenza delle componenti di ordine superiore diminuisce rapidamente con la divisione in elementi più piccoli. La correttezza di questa procedura è stata dimostrata in diverse analisi numeriche.

Elementi 3D

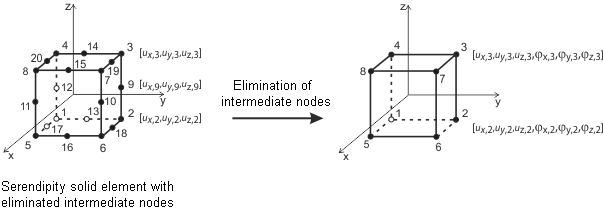
Gli elementi 3D sono utilizzati per i solidi. I seguenti tipi di elementi sono implementati in RFEM: tetraedro, pentaedro (prisma, piramide) ed esaedro. Per informazioni dettagliate sugli elementi applicati e sulle matrici, vedere Sevcik's 3D Elements with Rotational Degrees of Freedoms [8] per i dettagli. È possibile richiedere questa documentazione a Dlubal Software.

Elemento solido (Hexahedron)

In generale, tutti i gradi di libertà rotazionali devono essere considerati critici per i solidi. Poiché la deformazione di un solido è determinata esclusivamente dai vettori di spostamento, la rotazione di un nodo della mesh (ad esempio, a causa della torsione introdotta singolarmente) non influenza la deformazione all'interno del solido.