Una configuración de análisis estático (AE) especifica las reglas según las cuales se calculan los casos de carga y las combinaciones de carga. Se preestablecen tres tipos de análisis estándar.
Datos básicos
La pestaña Datos principales gestiona la configuración del análisis estructural y los parámetros de cálculo elementales.
Tipo de análisis
Esta sección de diálogo controla la teoría de cálculo según la cual se analizan los casos de carga y las combinaciones de carga. En la lista 'Tipo de análisis', hay tres planteamientos disponibles para su selección.
Geométricamente lineal
Al calcular según el análisis geométricamente lineal (primer orden), el equilibrio se analiza en un sistema estructural no deformado. Se realiza un análisis lineal porque las deformaciones de los componentes no se incluyen en el cálculo.
Los casos de carga se calculan de manera predeterminada según el análisis geométricamente lineal.
Segundo orden (P-Δ)
En el análisis 'estructural' de segundo orden, el equilibrio se determina en un sistema estructural deformado. Las deformaciones se suponen pequeñas. Los esfuerzos axiles en el sistema tienen un impacto en el aumento de los momentos flectores. Por lo tanto, este análisis entra en vigor cuando los esfuerzos axiles son significativamente mayores que los esfuerzos cortantes.
Las combinaciones de carga se calculan de forma no lineal de forma predeterminada según el análisis de segundo orden.
Grandes deformaciones
El análisis de grandes deformaciones (tercer orden o teoría de grandes deformaciones) considera los esfuerzos longitudinales y transversales en el cálculo. Después de cada paso de iteración, se crea la matriz de rigidez de un sistema deformado. Las cargas se gestionan de forma diferenciada: una carga definida en la dirección global mantiene su dirección si se retuercen elementos finitos. Si la carga actúa en la dirección de una barra local o del eje de la superficie, cambia su dirección según la torsión del elemento.
Si el modelo incluye barras de cable, se preestablece el cálculo según el análisis de grandes deformaciones.
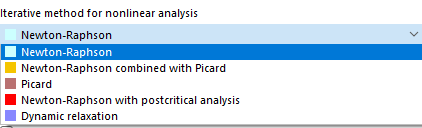
Método iterativo para análisis no lineal
Dependiendo del tipo de análisis, hay varios métodos disponibles para resolver el sistema de ecuaciones algebraicas no lineales.
Newton-Raphson
Se preestablece la aproximación según Newton-Raphson para el análisis de grandes deformaciones. El sistema de ecuaciones no lineal se resuelve numéricamente por medio de aproximaciones iterativas con tangentes. La matriz de rigidez tangencial se determina como función del estado actual de deformación; se invierte en cada ciclo de iteraciones. En la mayoría de casos, se alcanza una convergencia rápida (cuadrática).
Newton-Raphson combinado con Picard
Primero se aplica la aproximación según Picard. Después de algunas iteraciones, se cambia al método de Newton-Raphson. La idea básica de esta aproximación es utilizar el método de Picard relativamente 'insensible' para los primeros pasos de iteración con el fin de evitar mensajes de inestabilidad. A la aproximación inicial le sigue el método rápido según Newton-Raphson para buscar el estado último de equilibrio.
Picard
El método según Picard, también conocido como método de la secante, se puede entender como una aproximación en diferencias finitas del método de Newton-Raphson. Se considera la diferencia entre la ejecución de la iteración actual y original en el paso de incremento de carga actual. A menudo, la convergencia es más lenta en el método de cálculo según Newton-Raphson. Sin embargo, también resulta menos sensible a problemas no lineales, lo que hace que el cálculo sea más estable.
Newton-Raphson con análisis postcrítico
Este método es útil para resolver problemas poscríticos donde hay un rango de inestabilidad que superar. Si hay una inestabilidad disponible y no se puede invertir la matriz de rigidez, se usa la matriz de rigidez del último paso de iteración estable. Se continúa con el cálculo con la matriz hasta que se alcanza de nuevo un rango de estabilidad.
Relajación dinámica
El método final es adecuado para cálculos según el análisis de grandes deformaciones y para la resolución de problemas relacionados con las cuestiones poscríticas. En esta aproximación, se introduce un parámetro de tiempo artificial. Considerando la inercia y la amortiguación, el fallo se puede manejar como un problema dinámico. Esta aproximación usa el método explícito tiempo-integración; la matriz de rigidez no está invertida. No se admite ninguna parte del modelo para tener un peso específico de cero al cálculo con relajación dinámica.
Este método también incluye el amortiguamiento de Rayleigh que se puede definir mediante las constantes α y β según la siguiente ecuación con derivadas en el tiempo:
|
M |
Matriz de masas concentradas (diagonal) |
|
C |
Matriz de amortiguamiento diagonal C = α M + βdiag[K11 ( u ),K22 ( u ),...,Knn ( u )] |
|
K |
matriz de rigidez |
|
f |
Vector de fuerzas externas |
|
u |
Vector de desplazamiento discretizado |
Controles para análisis no lineal
El 'Número máximo de iteraciones' define cuántas ejecuciones de cálculo se realizan como máximo para un análisis según el segundo orden o análisis de grandes deformaciones, así como para objetos que actúan de forma no lineal. Cuando el cálculo alcanza el límite sin alcanzar el equilibrio, aparece el mensaje correspondiente. Luego, puede decidir si desea mostrar los resultados.
El 'Número de incrementos de carga' es relevante para los cálculos según el segundo orden o análisis de grandes deformaciones. Cuando se consideran grandes deformaciones, a menudo es difícil encontrar un equilibrio. Las inestabilidades se pueden evitar aplicando cargas en varios pasos. Por ejemplo, si especifica dos incrementos de carga, la mitad de la carga se aplica en el primer paso. Se itera hasta que se encuentra el equilibrio. Luego, en el segundo paso, se aplica la carga completa al sistema ya deformado y se repiten las iteraciones hasta que se alcanza el equilibrio.
Opciones I
En esta sección de diálogo, puede activar varias 'configuraciones especiales' para manipular los cálculos según el segundo orden o análisis de grandes deformaciones.
Modificar configuración estándar de precisión y tolerancia
Cuando selecciona la casilla 'Modificar configuración estándar de precisión y tolerancia', se agrega la pestaña Precisión y tolerancia al cuadro de diálogo, donde puede ajustar los criterios de convergencia.
Ignorar todas las no linealidades
Con la casilla 'Ignorar todas las no linealidades', puede desactivar las propiedades no lineales de los elementos para el cálculo. Por lo tanto, las piezas traccionadas, por ejemplo, permanecen en el modelo tan pronto como se produzcan los esfuerzos de compresión. Sin embargo, debe suprimir las propiedades no lineales solo con fines de prueba; por ejemplo, para encontrar la causa de una inestabilidad. A veces, un criterio de fallo definido incorrectamente es responsable de las interrupciones del cálculo.
Opciones II
Modificar carga por factor multiplicador
Después de marcar la casilla, puede definir un factor k por el cual se multiplicarán todas las cargas.
Las normas más antiguas pretenden multiplicar las cargas globalmente por un factor determinado para aumentar los efectos según el análisis de segundo orden para las comprobaciones de estabilidad. A su vez, el cálculo se debe realizar con las cargas de servicio. Se pueden cumplir ambos requisitos introduciendo un factor mayor que 1 y activando la casilla 'Dividir resultados entre factor de carga'.
Para los análisis según las normas actuales, la carga no se debe editar mediante factores. En su lugar, se deben tener en cuenta los coeficientes parciales de seguridad y de combinación para la superposición en las situaciones de proyecto.
Considerar efectos favorables debidos a tracción en barras
Los esfuerzos de tracción tienen un efecto favorable sobre los sistemas estructurales previamente deformados. De este modo, se reduce la deformación y se estabiliza la estructura. Normalmente, nos beneficiamos de este efecto en los cálculos según el análisis de grandes deformaciones y de segundo orden; por ejemplo, para naves con arriostramientos o estructuras en general sometidas a flexión. El alivio debido a los efectos del esfuerzo de tracción para las vigas con cerchas desde abajo (vigas con tirantes o cables de apoyo) puede resultar en una reducción no deseada de las deformaciones y esfuerzos internos.
Comprobación de estabilidad basada en el índice de deformación
Si selecciona la casilla, RFEM comprueba cómo se desarrollan las deformaciones a lo largo de las iteraciones durante el cálculo. Si los desplazamientos o giros aumentan bruscamente y superan un límite interno del programa, el cálculo se interrumpe con un mensaje de inestabilidad.
Intentar calcular la estructura inestable
Con esta casilla, puede intentar hacer que un modelo inestable sea calculable: En el primer paso del cálculo, RFEM aplica pequeños muelles que estabilizan el modelo para la primera iteración. Una vez que se alcanza un estado inicial estable, se quitan los muelles para iteraciones posteriores.
Desplazamientos debidos a cargas en barra de tipo 'Presión interna del tubo'.
La casilla es relevante para la carga en barra llamada presión interna del tubo. El efecto Bourdon describe el esfuerzo de una tubería doblada para enderezarse bajo la influencia de la presión. Tanto las tensiones perimetrales como las axiles causadas por la carga de presión interna conducen a una deformación longitudinal del tubo, considerando la rigidez del material y la deformación transversal.
Consulte este artículo técnico que describe un ejemplo de cómo se calcula la presión interna de los tubos.
Guardar resultados de todos los incrementos de carga
Si la carga se aplica de forma incremental (consulte los Controles para análisis no lineal), puede usar esta casilla para forzar la salida de resultados intermedios a fin de comprobar los resultados de los incrementos de carga individuales.
Solucionador directo asimétrico
Se usa un solucionador de ecuaciones directas asimétricas para un modelo de material no lineal (consulte el capítulo Comportamiento no lineal del material) con propiedades asimétricas para tracción y compresión. La casilla le permite usar este solucionador de ecuaciones también para otros modelos de material, como el modelo de material elástico no lineal isótropo.
Equilibrio para una estructura no deformada
La casilla le permite analizar una estructura que no se deforma, es decir, un sistema estructural cuyas deformaciones permanecen nulas. Esta opción de análisis puede ser útil cuando un sistema está sometido a tensión, por ejemplo, debido a un caso de carga, mientras que las deformaciones resultantes se pueden considerar atenuadas.
Un campo de aplicación para el cálculo del equilibrio de la estructura no deformada es el estado de tensiones primario del análisis geotécnico. Dentro del alcance de un caso de carga o combinación, hay que determinar las tensiones actuantes resultantes de la precarga del suelo. Sin embargo, las deformaciones de tal caso de carga o combinación no son de interés y, por lo tanto, no están sujetas a su uso posterior.
Configuración básica
La pestaña Configuración básica gestiona las especificaciones básicas para el cálculo.
Relación de cargas permanentes
La casilla 'Determinar para combinaciones de carga' ofrece la posibilidad de determinar la relación de una carga que actúa permanentemente en una combinación de cargas. Seleccione la combinación de cargas en la lista o cree una nueva combinación de cargas con el botón
![]() . Luego, en la lista 'Comparar valor del resultado', puede definir las razones que tienen un efecto estático o variable.
. Luego, en la lista 'Comparar valor del resultado', puede definir las razones que tienen un efecto estático o variable.
La relación de la carga permanente se puede considerar conforme a las normas en el cálculo.
Método para el sistema de ecuaciones
Ambas opciones controlan los métodos utilizados para resolver el sistema de ecuaciones. Para evitar malentendidos: Incluso cuando el sistema de ecuaciones se resuelve directamente, se realiza un cálculo iterativo si hay no linealidades o si los cálculos se realizan según el segundo orden o análisis de grandes deformaciones. 'Directo' e 'Iterativo' se refieren a la gestión de datos durante el cálculo.
El método de resolución de matrices que conduce más rápidamente a los resultados depende de la complejidad del modelo, así como del tamaño de la memoria principal (RAM) disponible. Para sistemas pequeños y medianos, el método directo es más eficiente.
Para sistemas muy grandes y complejos, el método iterativo conduce a resultados más rápidamente.
Teoría de flexión de placas
Las superficies se pueden calcular según las teorías de flexión de 'Mindlin' o 'Kirchhoff'. En el cálculo, según Mindlin, se incluyen las deformaciones por esfuerzo cortante; según Kirchhoff, no se tienen en cuenta. Por lo tanto, la opción de cálculo de Mindlin es adecuada para placas y láminas relativamente gruesas que se usan en construcciones sólidas, mientras que la opción Kirchhoff se recomienda para superficies que son relativamente delgadas, como las láminas de metal en construcciones de acero.
Configuración del método iterativo
Las casillas en esta sección de diálogo son importantes para el análisis de 'Segundo orden (P-Δ)'.
Referir esfuerzos internos a la estructura deformada
Los esfuerzos internos y los momentos de las barras se muestran generalmente en relación con la posición modificada de los sistemas de coordenadas de las barras que surgen en el sistema deformado. Si desea que la salida se refiera al sistema inicial sin deformar, puede definir los esfuerzos internos y momentos relevantes en la barra desactivando las casillas correspondientes.
Porcentaje de iteraciones del método Newton-Raphson en combinación con Picard
El método según Picard se basa en rigideces secantes, mientras que el método de Newton-Raphson se basa en rigideces tangentes. Cuando se selecciona la opción de cálculo Newton-Raphson combinado con Picard, se utilizan rigideces secantes en las primeras iteraciones antes de aplicar las rigideces tangentes para las iteraciones restantes. La razón de las primeras iteraciones con rigideces secantes está relacionada con el número total de iteraciones.
Conversión de la masa en carga
Las cargas se pueden definir no solo como fuerzas y momentos, sino también en forma de masas. Sin embargo, las masas no tienen ningún efecto en el análisis estructural. Si desea considerarlos, seleccione la casilla 'Masa activa'. Luego, introduzca el 'Factor en dirección' para describir el efecto de la masa. Por lo tanto, las masas se convierten en esfuerzos antes de que se inicie el cálculo y se incluyen en la determinación de los esfuerzos internos y momentos.
Utilice el botón
![]() para intercambiar entre la entrada del factor de masa y la entrada de la aceleración directamente. El nombre de los campos de entrada se ajusta en consecuencia.
para intercambiar entre la entrada del factor de masa y la entrada de la aceleración directamente. El nombre de los campos de entrada se ajusta en consecuencia.
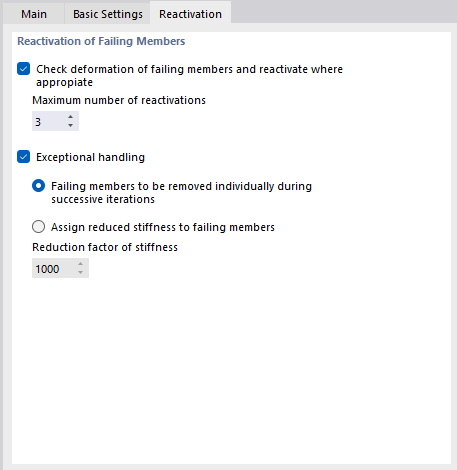
Reactivación
La pestaña Reactivación está disponible tan pronto como exista una barra con propiedades no lineales en el modelo. En esta pestaña, puede controlar cómo se tratan las barras defectuosas en el análisis.
Las barras defectuosas son a menudo la causa de problemas de inestabilidad, por ejemplo, cuando un modelo de barra es rigidizado mediante piezas traccionadas. Debido a las contracciones del pilar del pórtico por la carga vertical, las piezas traccionadas reciben pequeñas fuerzas de compresión en el primer paso del cálculo. Se quitarán del sistema. En el segundo paso, el modelo se vuelve inestable sin estas piezas traccionadas. Con las opciones en la sección de diálogo 'Reactivación de barras defectuosas', puede intentar realizar un cálculo sin mensaje de error.
Comprobar la deformación de las barras defectuosas y reactivarlas donde sea conveniente
RFEM analiza los desplazamientos de nudos en cada iteración. Por ejemplo, si los extremos de la barra de una pieza traccionada defectuosa se alejan entre sí, la barra se usa de nuevo en la matriz de rigidez.
La reactivación de barras puede ser problemática en algunos casos: Una barra se quita después de la primera iteración, se reactiva después de la segunda, se quita de nuevo después de la tercera iteración, y así sucesivamente. El cálculo ejecutaría este bucle hasta alcanzar el número máximo de iteraciones posible, sin converger. El 'Número máximo de reactivaciones' evita este efecto. Puede definir la frecuencia con la que se puede reinsertar un elemento de barra antes de que finalmente se quite de la matriz de rigidez.
Tratamiento excepcional
Si marca la casilla 'Tratamiento excepcional', puede seleccionar entre dos métodos para tratar las barras defectuosas. Se pueden combinar con la reactivación descrita anteriormente.
- Barras defectuosas para quitar individualmente durante iteraciones sucesivas
Después de la primera iteración, RFEM no quita, por ejemplo, todas las piezas traccionadas con una fuerza de compresión a la vez, sino solo la pieza traccionada con la mayor fuerza de compresión. En la segunda iteración, solo hay una barra menos en la matriz de rigidez. Posteriormente, se retira de nuevo la pieza traccionada con la mayor fuerza de compresión. De esta forma, el sistema suele mostrar un mejor comportamiento de convergencia debido a los efectos de redistribución.
Esta opción de cálculo requiere más tiempo porque se debe ejecutar el programa a través de un gran número de iteraciones. Además, se debe garantizar que se proporcione un Número máximo de iteraciones suficiente en la pestaña 'Datos principales'.
- Asignar rigidez reducida a las barras defectuosas
Las barras defectuosas no se quitan de la matriz de rigidez, sino que se asignan a una rigidez muy pequeña. Puede definirla en el campo 'Coeficiente de reducción de rigidez': Un factor de 1000 significa que la rigidez de la barra se reduce a 1/1000.
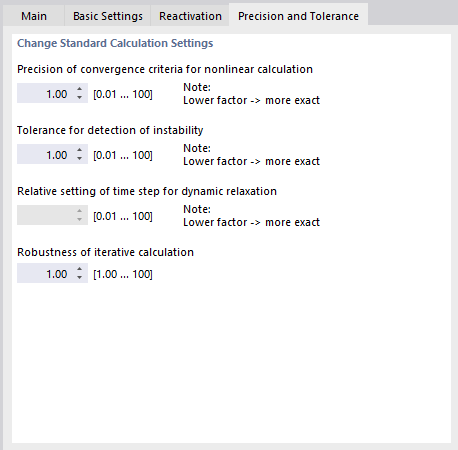
Precisión y tolerancia
La pestaña Precisión y tolerancia le permite influir en los parámetros de convergencia y tolerancia del cálculo. Sin embargo, debe cambiar la configuración predeterminada solo en casos excepcionales.
Precisión del criterio de convergencia del cálculo no lineal
Si actúan efectos no lineales o si se realizan análisis de segundo orden o de grandes deformaciones, se puede influir en el cálculo mediante criterios de convergencia.
El cambio de esfuerzos axiles en las dos últimas iteraciones se compara barra por barra. Tan pronto como el cambio alcanza una cantidad fraccional específica del esfuerzo axil máximo, se detiene el cálculo. Sin embargo, durante las iteraciones puede ocurrir que los esfuerzos axiles oscilen entre dos valores. Puede evitar este efecto de péndulo ajustando la 'sensibilidad'.
La precisión también afecta el criterio de convergencia para los cambios de deformación en los cálculos realizados según el análisis de grandes deformaciones, donde se consideran las no linealidades geométricas. El valor predeterminado es 1.0. El coeficiente mínimo es 0.01, el valor máximo es 100.0. Cuanto menor sea el valor, más cercano debe estar el término de convergencia al término de comparación. La precisión del resultado aumenta en consecuencia.
Tolerancia para la detección de la inestabilidad
Hay diferentes aproximaciones para analizar el comportamiento de estabilidad de un modelo. Sin embargo, ninguna de ellas es capaz de detectar las matrices de rigidez singulares con absoluta fiabilidad.
RFEM usa dos procedimientos para determinar la inestabilidad: Por un lado, los elementos de la diagonal principal de la matriz de rigidez siempre se comparan de forma absoluta con el mismo número en las iteraciones. Por otro lado, cada elemento de la diagonal principal se analiza en relación con el número adyacente. La tolerancia se puede ajustar en el campo. Cuanto menor sea el valor de tolerancia, más se acerca el límite de inestabilidad del modelo al lugar exacto de inestabilidad. La precisión del resultado aumenta en consecuencia.
Configuración relativa del paso de tiempo para la relajación dinámica
El parámetro de tiempo controla el cálculo según el método de relajación dinámica. Cuanto menor sea el valor, menor es el paso de tiempo en el que se registran todas las fluctuaciones de respuesta. La precisión de los resultados aumenta en consecuencia.
Solidez del cálculo iterativo
En el caso de problemas de convergencia con el método de Newton-Raphson, se puede reforzar la robustez para evitar que la solución "salte". Al reducir el valor, se reduce el número de soluciones posibles en caso de que exista una rama de la solución horizontal no convergente y, por lo tanto, también se reduce la posibilidad de un resultado válido dentro de las iteraciones especificadas. Puede que sea necesario aumentar el número máximo de iteraciones.