Zurück zu Online-Handbüchern

5097x

000076

Dipl.-Ing. Frank Faulstich

14. Dezember 2023

Handbuch wählen

Übersicht

Benutzeroberfläche und Einstellungen

Dlubal Center

Modell-Basisangaben

Struktur

Imperfektionen

Lastfälle und Kombinationen

Lastassistenten

Lasten

Berechnung

Ergebnisse

Hilfsobjekte

Programmfunktionen

Ergebnisauswertung

Ausdruckprotokolle

Nichtlineares Materialverhalten

Wenn bei den Modell-Basisangaben das Analyse-Add-On Nichtlineares Materialverhalten aktiviert ist (Lizenz erforderlich), stehen neben den Materialmodellen 'Isotrop | Linear elastisch' und 'Orthotrop | Linear elastisch' in der Liste der Materialmodelle weitere Möglichkeiten zur Auswahl.

Materialmodelle für Analyse-Add-On 'Nichtlineares Materialverhalten'

Wenn Sie in RFEM nichtlineare Materialmodelle verwenden, dann wird immer eine iterative Berechnung durchgeführt. Je nach Materialmodell wird ein anderer Zusammenhang zwischen Spannungen und der Dehnungen definiert.

Die Steifigkeit der finiten Elemente wird im Laufe der Iterationen immer wieder angepasst, bis die Spannungs-Dehnungs-Beziehung eingehalten ist. Die Anpassung erfolgt immer für ein ganzes Flächen- oder Volumenelement. Bei der Auswertung der Spannungen sollte deswegen immer die Glättungsart Konstant in Netzelementen verwendet werden.

Ergebnisglättung

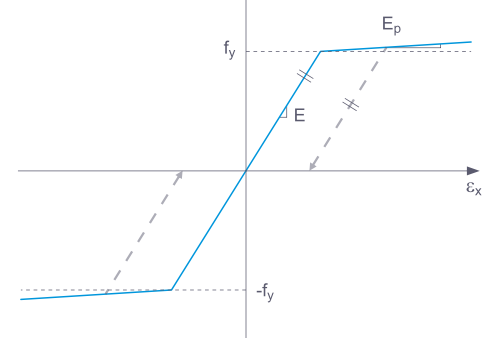
Einige Materialmodelle in RFEM werden mit 'plastisch', andere mit 'nichtlinear elastisch' bezeichnet.

Wird ein Bauteil mit einem nichtlinear elastischen Material wieder entlastet, dann geht die Dehnung auf dem gleichen Pfad zurück. Bei der vollständigen Entlastung bleibt keine Dehnung zurück.

Spannungs-Dehnungs-Diagramm nichtlinear elastisch

Bei der Entlastung eines Bauteils mit einem plastischen Materialmodell bleibt nach der vollständigen Entlastung eine Dehnung zurück.

Spannungs-Dehnungs-Diagramm plastisch

Die Be- und Entlastung kann mit dem Add-On Analyse von Bauzuständen simuliert werden.

Hintergrundinformationen zu den nichtlinearen Materialmodellen sind im Fachbeitrag Fließgesetze im Materialmodell Isotrop nichtlinear elastisch zu finden.

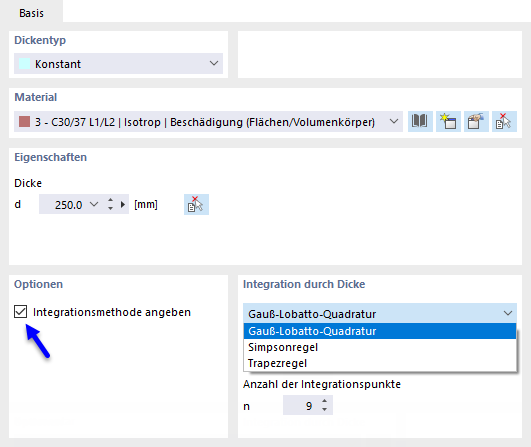
Die Schnittgrößen in Platten mit nichtlinearem Material ergeben sich aus der numerischen Integration der Spannungen über die Plattendicke. Um die Integrationsmethode für die Dicke festzulegen, haken Sie im Dialog 'Dicke bearbeiten' die Option Integrationsmethode angeben an. Damit stehen folgende Integrationsmethoden zur Auswahl:

Gauß-Lobatto-Quadratur
Simpsonregel
Trapezregel

Integrationsmethode für Flächendicke festlegen

Des Weiteren können Sie die 'Anzahl der Integrationspunkte' über die Plattendicke von 3 bis 99 vorgeben.

Info

Eine theoretische Erklärung zu den einzelnen Integrationsmethoden finden Sie im Handbuch Mehrschichtige Flächen.

Isotrop plastisch (Stäbe)

Wenn Sie in der Dropdown-Liste 'Materialmodell' den Eintrag Isotrop | Plastisch (Stäbe) auswählen, dann wird das Register für die Eingabe der nichtlinearen Materialparameter aktiv.

Nichtlineares Materialmodell aktivieren

Nichtlineare Materialparameter definieren

In diesem Register definieren Sie das Spannungs-Dehnungs-Diagramm. Hierfür stehen die folgenden Möglichkeiten zur Auswahl:

Standard
Bilinear
Diagramm

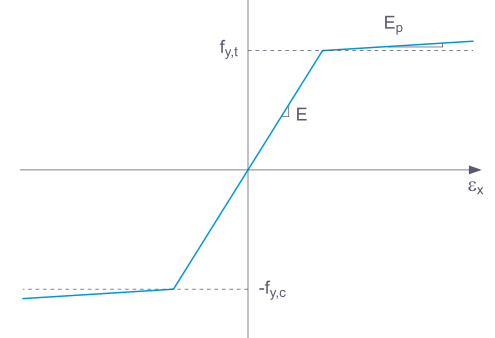
Wenn Standard ausgewählt wurde, dann nutzt RFEM ein bilineares Materialmodell. Für den Elastizitätsmodul E und die Fließgrenze f_y werden die Werte aus der Materialdatenbank genutzt. Aus numerischen Gründen verläuft der Ast nicht genau horizontal, sondern hat einen kleinen Anstieg E_p.

Wenn Sie die Werte für die Steckgrenze und den Elastizitätsmodul verändern möchten, dann aktivieren Sie im Register 'Basis' das Kontrollfeld Benutzerdefiniertes Material.

Benutzerdefiniertes Material aktivieren

Bei der bilinearen Definition können Sie auch den Wert für E_p eingegeben.

Komplexere Zusammenhänge zwischen Spannung und Dehnung definieren Sie mittels Spannungs-Dehnungs-Diagramm. Wenn Sie diese Option auswählen, dann wird das Register 'Spannungs-Dehnungs-Diagramm' eingeblendet.

Benutzerdefiniertes Spannungs-Dehnungs-Diagramm eingeben

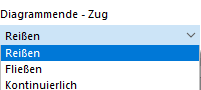
Definieren Sie in jeder Zeile einen Punkt für die Spannungs-Dehnungs-Beziehung. Wie das Diagramm nach dem letzten Definitionspunkt weiter verlaufen soll, können Sie in der Liste 'Diagrammende' unterhalb des Diagramms auswählen:

Verlauf nach dem letzten Definitionspunkt

Beim 'Reißen' springt die Spannung nach dem letzten Definitionspunkt zurück auf null. 'Fließen' bedeutet, dass die Spannung bei zunehmender Dehnung konstant bleibt. 'Kontinuierlich' heißt, dass die Kurve mit der Steigung des letzten Abschnitts weiter verläuft.

Info

In diesem Materialmodell bezieht sich das Spannungs-Dehnungs-Diagramm auf die Längsspannung σ_x. Unterschiedliche Fließgrenzen für Zug und Druck können mit diesem Materialmodell nicht berücksichtigt werden.

Isotrop plastisch (Flächen/Volumenkörper)

Wenn Sie in der Dropdown-Liste 'Materialmodell' den Eintrag Isotrop | Plastisch (Flächen/Volumenkörper) auswählen, dann wird das Register für die Eingabe der nichtlinearen Materialparameter aktiv.

Plastisches Materialmodell auswählen

Wählen Sie zunächst die 'Spannungsversagenshypothese' aus. Zur Auswahl stehen diese Hypothesen:

von Mises (Gestaltänderungsenergie-Hypothese)
Tresca (Schubspannungshypothese)
Drucker-Prager
Mohr-Coulomb

Spannungsversagenshypothese festlegen

Wenn Sie von Mises auswählen, dann wird im Spannungs-Dehnungs-Diagramm folgende Spannung verwendet:

Flächen:

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Vergleichsspannung aus Grundspannungen nach von Mises

Volumenkörper:

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Vergleichsspannung σ_v,Mises aus Grundspannungen

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Vergleichsspannung σ_v,Mises aus Hauptspannungen

Nach der Hypothese von Tresca wird diese Spannung verwendet:

Flächen:

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Vergleichsspannung nach Tresca

Volumenkörper:

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Vergleichsspannung σ_v,Tresca

Nach der Hypothese von Drucker-Prager wird diese Spannung für Flächen und Volumen verwendet:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Grenzspannung für Druck
σ_t	Grenzspannung für Zug

Fließkriterium nach Drucker-Prager

Nach der Hypothese von Mohr-Coulomb wird folgende Spannung für Flächen und Volumen verwendet:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr–Coulomb

Isotrop nichtlinear elastisch (Stäbe)

Die Funktionsweise entspricht weitgehend der des Materialmodells Isotrop plastisch (Stäbe). Im Unterschied zu diesem verbleibt aber nach der Entlastung keine plastische Dehnung.

Isotrop nichtlinear elastisch (Flächen/Volumenkörper)

Die Funktionsweise entspricht weitgehend der des Materialmodells Isotrop plastisch (Flächen/Volumenkörper). Im Unterschied zu diesem verbleibt aber nach der Entlastung keine plastische Dehnung.

Isotrop Beschädigung (Flächen/Volumenkörper)

Im Unterschied zu anderen Materialmodellen ist das Spannungs-Dehnungs-Diagramm für dieses Materialmodel nicht antimetrisch zum Ursprung. Somit kann mit diesem Materialmodel beispielsweise das Verhalten von Stahlfaserbeton abgebildet werden. Ausführliche Hinweise zum Modellieren von Stahlfaserbeton finden Sie im Fachbeitrag Materialeigenschaften von Stahlfaserbeton.

Materialmodell 'Isotrop | Beschädigung'

Bei diesem Materialmodell wird die isotrope Steifigkeit mit einem skalaren Schädigungsparameter abgemindert. Dieser Schädigungsparameter bestimmt sich aus dem Verlauf der Spannung, die im Diagramm festgelegt ist. Dabei wird nicht die Richtung der Hauptspannungen berücksichtigt, sondern die Schädigung erfolgt vielmehr in Richtung der Vergleichsdehnung, die auch die dritte Richtung senkrecht zur Ebene erfasst. Der Zug- und Druckbereich des Spannungstensors wird separat behandelt. Es gelten jeweils unterschiedliche Schädigungsparameter.

Die 'Referenzelementgröße' steuert, wie die Dehnung im Rissbereich auf die Länge des Elements skaliert wird. Mit dem voreingestellten Wert null erfolgt keine Skalierung. Damit wird das Materialverhalten des Stahlfaserbetons realitätsnah abgebildet.

Theoretische Hintergründe zum Materialmodell 'Isotrop Beschädigung' finden Sie im Fachbeitrag Nichtlineares Materialmodell Schädigung.

Orthotrop plastisch (Flächen) / Orthotrop plastisch (Volumenkörper)

Das Materialmodell nach Tsai-Wu vereint plastische und orthotrope Eigenschaften. Damit sind spezielle Modellierungen von Werkstoffen mit anisotroper Charakteristik wie faserverstärkter Kunststoff oder Holz möglich.

Beim Plastizieren des Materials bleiben die Spannungen konstant. Es erfolgt eine Umlagerung in Abhängigkeit von den Steifigkeiten, die in die einzelnen Richtungen vorliegen.

Materialmodell 'Orthotrop | Plastisch (Flächen)'

Materialmodell 'Orthotrop | Plastisch (Volumenkörper)'

Der elastische Bereich entspricht dem Materialmodell Orthotrop linear elastisch (Volumenkörper) . Für den plastischen Bereich gilt folgende Fließbedingung nach Tsai-Wu:

Flächen (2D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, ebener Spannungszustand

Volumenkörper (3D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, räumlicher Spannungszustand

Sämtliche Festigkeiten sind positiv zu definieren.

Die Fließbedingung kann man sich als ellipsenförmige Fläche im sechsdimensionalen Spannungsraum vorstellen. Wird eine der drei Spannungskomponenten als konstanter Wert angesetzt, kann die Fläche auf einen dreidimensionalen Spannungsraum projiziert werden.

Ist der Wert für f_y(σ) nach Gleichung Tsai-Wu, ebener Spannungszustand kleiner als 1, so liegen die Spannungen im elastischen Bereich. Der plastische Bereich ist erreicht, sobald f_y(σ) = 1. Werte größer als 1 sind unzulässig. Das Modell verhält sich ideal-plastisch, das heißt es findet keine Versteifung statt.

Mauerwerk

Wenn bei den Modell-Basisangaben das Bemessungs-Add-On Mauerwerksbemessung aktiviert ist (Lizenz erforderlich), stehen für den Materialtyp 'Mauerwerk' die Materialmodelle 'Isotrop | Mauerwerk | Plastisch (Flächen)' und 'Orthotrop | Mauerwerk | Plastisch (Flächen)' zur Auswahl.