返回在线手册

此页面有帮助吗？

5988x

000076

Dipl.-Ing.弗兰克·福尔施蒂奇

2023-12-14

选择手册

概览

图形用户界面和设置

Dlubal 中心

模型 - 基本数据

结构

缺陷

荷载工况和组合

荷载向导

荷载

结构对象

计算

结果

辅助对象

程序功能

结果查看

打印报告

材料非线性

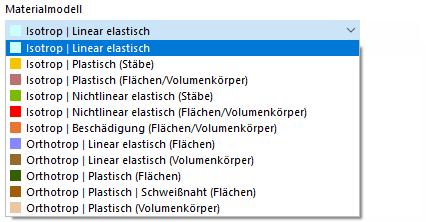
材料模型

Wenn bei den Modell-Basisangaben das Analyse-Add-On Nichtlineares Materialverhalten aktiviert ist (Lizenz erforderlich), stehen neben den Materialmodellen 'Isotrop | Linear elastisch' und 'Orthotrop | Linear elastisch' in der Liste der Materialmodelle weitere Möglichkeiten zur Auswahl.

“非线性材料行为”分析模块材料模型

计算方法

Wenn Sie ein nichtlineares Materialmodell verwenden, wird immer eine iterative Berechnung durchgeführt. 不同的材料弹塑性模型提供了不同的应力应变关系(本构关系)。

材料的弹塑性模型中，刚度并不是一个定值。在进行计算时，程序需要不断修正结构的刚度矩阵，反复迭代以得到满足用户定义的应力-应变关系的数值解。在迭代计算应力过程中，如果模型中存在面和实体单元， Bei der Auswertung der Spannungen sollte deshalb immer die Glättungsart Konstant in Netzelementen verwendet werden.

结果平滑

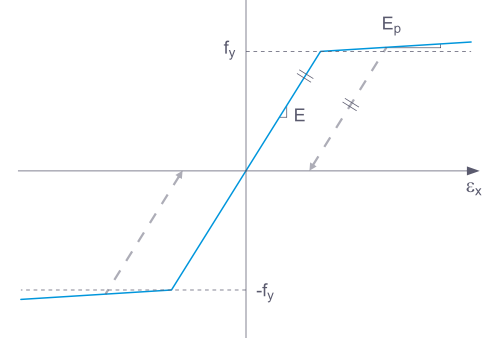
RFEM 中的非线性材料模型分为【塑性】和【非线性弹性】。 Wird ein Bauteil mit einem nichtlinear elastischen Material wieder entlastet, geht die Dehnung auf dem gleichen Pfad zurück. 不存在残余的塑性变形。

应力-应变图，非线性弹性

塑性材料在卸载后，存在不可恢复的塑性应变。塑性材料卸载时应力应变曲线将沿下图的灰色路径。

应力-应变图，塑性

Die Be- und Entlastung kann mit dem Add-On Analyse von Bauzuständen simuliert werden.

Hintergrundinformationen zu den nichtlinearen Materialmodellen sind im Fachbeitrag Fließgesetze im Materialmodell Isotrop nichtlinear elastisch zu finden.

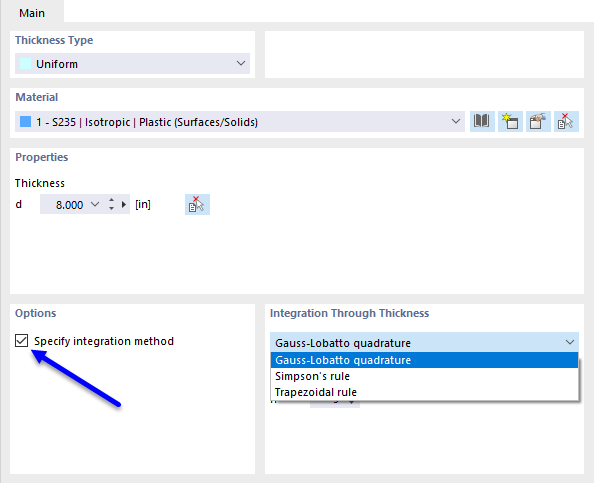
Die Schnittgrößen in Platten mit nichtlinearem Material ergeben sich aus der numerischen Integration der Spannungen über die Plattendicke. Um die Integrationsmethode für die Dicke festzulegen, haken Sie im Dialog 'Dicke bearbeiten' die Option Integrationsmethode angeben an. Damit stehen folgende Integrationsmethoden zur Auswahl:

高斯-洛巴托积分(Gauss-Lobatto quadrature)
辛普森法(Simpson's rule)
梯形法

定义面厚度的积分方法

Des Weiteren können Sie die 'Anzahl der Integrationspunkte' über die Plattendicke von 3 bis 99 vorgeben.

信息

Eine theoretische Erklärung zu den einzelnen Integrationsmethoden finden Sie im Handbuch Mehrschichtige Flächen.

各向同性塑性(杆件)

Wenn Sie in der Dropdown-Liste 'Materialmodell' den Eintrag Isotrop | Plastisch (Stäbe) auswählen, dann wird das Register für die Eingabe der nichtlinearen Materialparameter aktiv.

激活非线性材料模型

定义非线性材料参数

在【各向同性-塑性(杆件)】选项卡下，可以选择将应力-应变曲线定义为以下类型：

标准化
双线性
图表

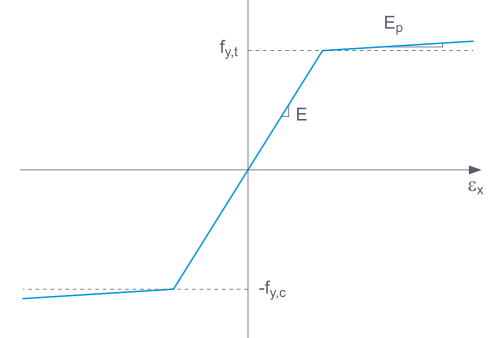
选择应力-应变曲线为【基本】时，RFEM 使用双折线应力-应变曲线。第一段折线的斜率为弹性模量 E，终点对应的应力为屈服强度 fy 。 Für den Elastizitätsmodul E und die Fließgrenze f_y werden die Werte aus der Materialdatenbank genutzt. Aus numerischen Gründen verläuft der Ast nicht genau horizontal, sondern hat einen kleinen Anstieg E_p.

用户可以通过勾选【用户自定义材料】来修改弹性模量 E 和屈服强度 fy。

激活用户自定义材料

Bei der bilinearen Definition können Sie auch den Wert für E_p eingegeben.

选择应力-应变曲线为【应力-应变图】时，用户可以定义更复杂的应力-应变关系。选择该选项后，会出现【应力-应变图】选项卡，用户可以在该选项卡下以表格的形式定义应力-应变曲线。

输入用户自定义的应力-应变图

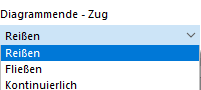
该表格中的每一行对应着应力-应变曲线上的一个点。应力-应变曲线在输入的最后一个点之后的曲线走向可以在右侧图标下方的【图表开始-受拉】下拉菜单中选择。

最后一个定义点之后的曲线变化

选择【撕裂】，最后一点之后的应力会变成零。【屈服】表示最后一点之后的应力保持恒定。【连续】表示最后一点之后的应力-应变曲线以该点处的斜率继续延伸。

信息

需要说明的是，该材料模型的应力-应变曲线中的应力指的是正应力 σ_x。该材料模型不适用于抗压强度和抗拉强度不同的材料。

各向同性塑性(面/实体)

Wenn Sie in der Dropdown-Liste 'Materialmodell' den Eintrag Isotrop | Plastisch (Flächen/Volumenkörper) auswählen, dann wird das Register für die Eingabe der nichtlinearen Materialparameter aktiv.

选择塑性材料模型

在【应力破坏假设】下，用户可以选择不同的屈服准则：

von Mises（米塞斯屈服准则）
Tresca（屈雷斯加屈服准则）
Drucker-Prager
Mohr-Coulomb

定义应力破坏假设

Wenn Sie von Mises auswählen, werden im Spannungs-Dehnungs-Diagramm folgende Spannungen verwendet:

面积

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

根据 von Mises 由基本应力计算等效应力

实体

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

根据基本应力计算等效应力 σ_v,Mises

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

由主应力计算的等效应力 σ_v,Mises

Nach der Hypothese von Tresca werden diese Spannungen verwendet:

面积

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

根据 Tresca 的等效应力

实体

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

等效应力 σ_v,Tresca

选择 Drucker-Prager 时，应力-应变曲线中的应力二维和三维状态下表达式如下：

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Grenzspannung für Druck
σ_t	Grenzspannung für Zug

Drucker-Prager 屈服准则

选择 Mohr-Coulomb 时，应力-应变曲线中的应力二维和三维状态下表达式如下：

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

莫尔-库伦

各向同性非线性弹性(杆件)

【各向同性|非线性弹性(杆件)】材料模型与塑性(杆件)】材料模型基本相同，不同之处在于【各向同性|非线性弹性(面/实体)】材料模型的应力应变曲线不存在卸载的塑性应变。

各向同性非线性弹性(面/实体)

【各向同性|非线性弹性(面/实体)】材料模型与塑性(面/实体)】材料模型基本相同，不同之处在于【各向同性|非线性弹性(面/实体)】材料模型的应力应变曲线不存在卸载的塑性应变。

各向同性损伤(面/实体)

与其他材料模型不同，【各向同性|损伤(面/实体)】材料模型的应力应变曲线不关于原点中心对称。该材料模型可以用于模拟受拉强度与受压强度不同的材料，例如钢筋混凝土。 Ausführliche Hinweise zum Modellieren von Stahlfaserbeton finden Sie im Fachbeitrag Materialeigenschaften von Stahlfaserbeton.

材料模型“各向同性” | 损伤"

使用损伤因子这一标量参数来考虑材料的失效特性。一般情况下，存在于材料内部的损伤(微裂缝、空腔)是有方向性的。当损伤变量与材料受力面的法向相关时，为各向异性损伤；当损伤变量与法向无关时，为各向同性损伤，这时的损伤变量为一标量。规范附录中给出的混凝土应力-应变曲线是根据应变等效性推导的损伤演化方程得出的。

【参照单元尺寸】影响了非线性分析中的单元尺寸效应。程序默认【参照单元尺寸】为 0，以便真实模拟钢筋混凝土的材料性能。

Theoretische Hintergründe zum Materialmodell 'Isotrop Beschädigung' finden Sie im Fachbeitrag Nichtlineares Materialmodell Schädigung.

正交各向异性塑性(面)和正交各向异性塑性(实体)

程序根据 Tsai-Wu 失效准则给出了【正交各向异性|塑性(面)】和【正交各向异性|塑性(实体)】的材料模型。该材料模型适用于编织材料、木材等具有各向异性的材料。

当材料进入塑性后，应力不再随应变增长，保持恒定。

材料模型“正交各向异性” | 塑性（面）"

材料模型 ' 正交各向异性 | 塑料（实体）'

Der elastische Bereich entspricht dem Materialmodell Orthotrop linear elastisch (Volumenkörper) . 当材料的应力满足以下条件，即认为材料进入塑性：

面积

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu，平面应力状态

实体

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu，应力空间状态

Sämtliche Festigkeiten sind positiv zu definieren.

Die Fließbedingung kann man sich als ellipsenförmige Fläche im sechsdimensionalen Spannungsraum vorstellen. 投影在各个平面上为一个椭圆。

Ist der Wert für f_y(σ) nach Gleichung Tsai-Wu, ebener Spannungszustand kleiner als 1, so liegen die Spannungen im elastischen Bereich. Der plastische Bereich ist erreicht, sobald f_y(σ) = 1. Werte größer als 1 sind unzulässig. 即塑性阶段应力不随着应变继续变化。

Orthotrop plastisch Schweißnaht (Flächen)

Dieses Materialmodell findet bei Analysen mit dem Add-On Stahlanschlüsse Verwendung, um das Verhalten von Schweißnähten normengerecht abzubilden. In der Ersatzfläche entstehen nur Spannungen, die den Spannungskomponenten σ_⊥, τ_⊥ und τ_|| der Schweißnaht entsprechen. In den übrigen Spannungsrichtungen geht die Steifigkeit der Ersatzfläche gegen null.

材料模型“正交各向异性 | 塑性 | 焊缝(面)”

Im Register 'Orthotrop | Plastisch | Schweißnaht (Flächen)' können Sie die Parameter für die Berücksichtigung der plastischen Materialverfestigung bei Schweißnähten festlegen, beispielsweise die Grenzwerte f_ekv und f_x für den Spannungsnachweis nach dem "richtungsbezogenen Verfahren" gemäß EN 1993-1-8 [1] für Schweißnähte, modifiziert um einen plastischen Anteil (siehe auch Fachbeitrag Nachweis von Kehlnähten).

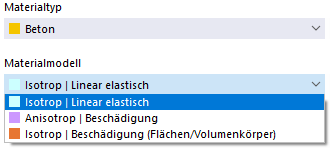
混凝土

Für den Materialtyp 'Beton' stehen die nichtlinearen Materialmodelle 'Anisotrop | Beschädigung' und 'Isotrop | Beschädigung (Flächen/Volumenkörper)' zur Auswahl.

混凝土的材料模型

Die beiden Materialmodelle sind im Kapitel Materialtyp und Materialmodell des Beton-Handbuchs bzw. oben im Abschnitt Isotrop Beschädigung beschrieben.

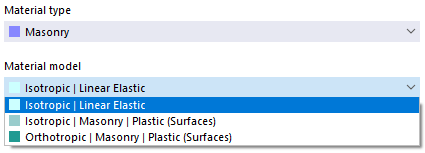
砌体结构

Wenn bei den Modell-Basisangaben das Bemessungs-Add-On Mauerwerksbemessung aktiviert ist (Lizenz erforderlich), stehen für den Materialtyp 'Mauerwerk' die nichtlinearen Materialmodelle 'Isotrop | Mauerwerk | Plastisch (Flächen)' und 'Orthotrop | Mauerwerk | Plastisch (Flächen)' zur Auswahl.