用户使用手册 RFEM 6

返回在线手册

8359x

002715

2023-12-15

选择手册

图形用户界面和设置

模型 - 基本数据

荷载工况和组合

应力

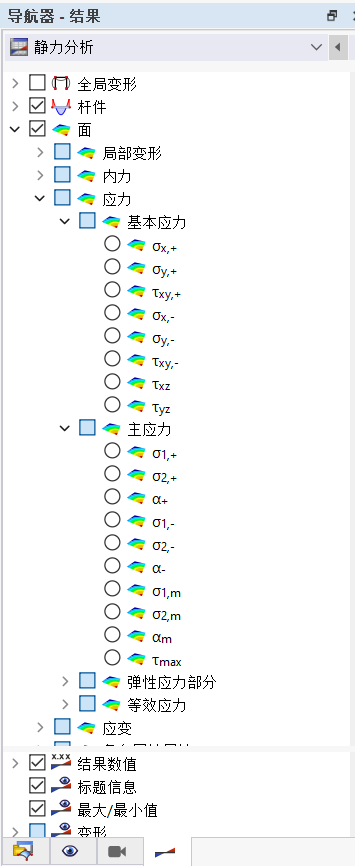
用户可以在导航器-结果中勾选面的内力，以图形形式在结果中显示面的内力。表格中的结果显示情况遵循用户在【结果表管理器】中的设置。

在导航器-结果中勾选面的应力

在导航器-结果中勾选面的应力

在表格中查看面的应力结果

在表格中查看面的应力结果

面的应力有以下几种类型：

基本应力：参照面的局部坐标系表达的应力
主应力：参照面的主轴坐标系表达的应力
弹性应力部分：仅由面的弯矩或内力引起的应力
等效应力：根据各种强度理论得到的等效应力

基本应力

面的基本应力参照面的局部坐标系进行表达，对于曲面参照有限元网格的局部坐标系进行表达。（见图显示有限元坐标系 )。

基本应力、面的“+”“-”表面示意见图面内力和面应力。基本应力与面的基本内力、弯矩的关系如下：

σ_{x, +} = \frac{n_{x}}{d} + \frac{6 m_{x}}{d^{2}}

d

面的厚度

σ_x,+ (在面的“+”表面上的沿面局部轴x轴方向的正应力)

σ_{y, +} = \frac{n_{y}}{d} + \frac{6 m_{y}}{d^{2}}

σ_y,+ (在面的“+”表面上的沿面局部轴y轴方向的正应力)

σ_{x, -} = \frac{n_{x}}{d} - \frac{6 m_{x}}{d^{2}}

σ_x,- (在面的“-”表面上的沿面局部轴x轴方向的正应力)

σ_{y, -} = \frac{n_{y}}{d} - \frac{6 m_{y}}{d^{2}}

应力 σ_y,-(在面的“-”表面上沿面局部轴y轴的正应力)

τ_{x y, +} = \frac{n_{x y}}{d} + \frac{6 m_{x y}}{d^{2}}

τ_xy,+(在面的“+”表面上的扭应力)

τ_{x y, -} = \frac{n_{x y}}{d} - \frac{6 m_{x y}}{d^{2}}

τ_xy,-(在面的“-”表面上的扭应力)

τ_{x z} = \frac{3 v_{x}}{2 d}

τ_xz(该应力位于面的x面上，方向沿面的局部z方向，即沿面的厚度方向)

τ_{y z} = \frac{3 v_{y}}{2 d}

τ_yz(该应力位于面的y面上，方向沿面的局部z方向，即沿面的厚度方向)

主应力

主轴为面基本应力随局部坐标轴变化而取到正应力极值时的局部坐标轴。主轴1（最大值）和主轴2（最小值）正交。主轴方向 α 可以通过轨迹以图形方式显示（如图显示主轴 )。

主应力与基本应力关系如下：

σ_{1, +} = \frac{1}{2} [σ_{x, +} + σ_{y, +} + \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{x y, +}}^{2}}]

在面的“+”表面上，主应力σ_1,+与基本应力之间的关系

σ_{2, +} = \frac{1}{2} [σ_{x, +} + σ_{y, +} - \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{x y, +}}^{2}}]

在面的“+”表面上，主应力σ_2,+与基本应力之间的关系

α_{+} = \frac{1}{2} \arctan 2 (\frac{2 τ_{x y, +}}{σ_{x, +} - σ_{y, +}}) \in (- 90 °, 90 °]

面“+”表面上，主轴与面局部坐标轴之间的夹角α₊

σ_{1, -} = \frac{1}{2} [σ_{x, -} + σ_{y, -} + \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{x y, -}}^{2}}]

在面的“-”表面上，主应力σ_1,-与基本应力之间的关系

σ_{2, -} = \frac{1}{2} [σ_{x, -} + σ_{y, -} - \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{x y, -}}^{2}}]

在面的“-”表面上，主应力σ_2,-与基本应力之间的关系

α_{-} = \frac{1}{2} \arctan 2 (\frac{2 τ_{x y, -}}{σ_{x, -} - σ_{y, -}}) \in (- 90 °, 90 °]

面“-”表面上，主轴与面局部坐标轴之间的夹角α_-

σ_{1, m} = \frac{1}{2} [σ_{x, m} + σ_{y, m} + \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{x y, m}}^{2}}]

膜应力 σ_1,m与基本应力之间的关系

σ_{2, m} = \frac{1}{2} [σ_{x, m} + σ_{y, m} - \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{x y, m}}^{2}}]

膜应力 σ_2,m与基本应力之间的关系

α_{m} = \frac{1}{2} \arctan 2 (\frac{2 τ_{x y, m}}{σ_{x, m} - σ_{y, m}}) \in (- 90 °, 90 °]

主轴与面局部坐标轴之间的夹角 α_m(膜应力取极值时)

τ_{\max} = \sqrt{{τ_{x z}}^{2} + {τ_{y z}}^{2}}

最大剪应力 τ_max(沿面厚度方向的应力)

其他应力/弹性应力分量

仅由面的弯矩或内力引起的应力，参照面的局部坐标系进行表达，分析曲面时，参照有限元网格的坐标轴进行表达。

弯矩和轴力引起的应力如下：

σ_{x, b} = \frac{6 m_{x}}{d^{2}}

d

面的厚度

弯矩 m_x产生的应力 σ_x,b

σ_{y, b} = \frac{6 m_{y}}{d^{2}}

弯矩 m_y产生的应力 σ_y,b

τ_{x y, b} = \frac{6 m_{x y}}{d^{2}}

扭矩 m_xy产生的应力 τ_xy,b

σ_{x, m} = \frac{n_{x}}{d}

轴力 n_x引起的膜应力 σ_x,m

σ_{y, m} = \frac{n_{y}}{d}

轴力 n_y引起的膜应力 σ_y,m

τ_{x y, m} = \frac{n_{x y}}{d}

剪切流 n_xy产生的应力 τ_{xy, m}

等效应力

根据四种强度准则，得到的平面应力状态下的基本应力。

von Mises

von Mises是基于剪切应变能的一种等效应力。 von Mises强度理论属于第四强度理论的一种，认为当材料中某一点的形状改变比能达到单向应力状态的极限值，材料发生屈服破坏。随着弹性体发生变形而积蓄在其内部的能量称为变形能。在单位变形体体积内所积蓄的变形能称为变形比能。该强度准则是最著名和最常用的强度准则。它适用于所有非脆性材料(即塑性材料，如不锈钢等)。常用于分析建筑工程的钢结构是否屈服破坏。 von Mises 假设不适用于在所有方向上都具有相等主应力(即静水应力条件，σ₁=σ₂=σ₃)的情况，在这种情况下计算出的Mises等效应力为零。例如不锈钢，本身是塑性材料，大多数情况下都会因为产生屈服而失效，但根据von Mises应力计算公式，若σ₁=σ₂=σ₃，即三个方向受相同大小的拉力或压力（例如不锈钢制成的螺钉受拉时，螺纹根部因应力集中而引起三向拉伸），Mises等效应力始终等于零，显然不能用von Mises应力作为失效判据。这种情况下，不锈钢将会直接断裂，不会经历屈服、颈缩过程，需使用脆性材料失效准则来判定是否失效，此时需使用第一强度理论进行判定。

平面应力状态下，von Mises等效应力与主应力之间的关系如下：

σ_{v, Mises, Max} = \max (σ_{v, Mises, +}; σ_{v, Mises, -})

最大等效米塞斯应力 σ_v,Mises,max

σ_{v, Mises, +} = \sqrt{{σ_{x, +}}^{2} + {σ_{y, +}}^{2} - σ_{x, +} σ_{y, +} + 3 {τ_{x y, +}}^{2}}

面的“+”表面上的等效米塞斯应力 σ_v,Mises,+

σ_{v, Mises, -} = \sqrt{{σ_{x, -}}^{2} + {σ_{y, -}}^{2} - σ_{x, -} σ_{y, -} + 3 {τ_{x y, -}}^{2}}

面的“-”表面上的等效米塞斯应力 σ_v,Mises,-

σ_{v, Mises, m} = \sqrt{{σ_{x, m}}^{2} + {σ_{y, m}}^{2} - σ_{x, m} σ_{y, m} + 3 {τ_{x y, m}}^{2}}

根据米塞斯准则得到的等效膜应力 σ_v,Mises,m

Tresca

Tresca理论也被称为最大剪应力理论，当材料中一点的剪应力达到单向应力状态的极限值，材料发生屈服破坏。该强度理论适用于脆性材料，常用于机械工程。

平面应力状态下Tresca 等效应力与主应力之间的关系如下：

σ_{v, Tresca, Max} = \max (σ_{v, Tresca, +}; σ_{v, Tresca, -})

最大Tresca等效应力σ_v,Tresca,max

σ_{v, Tresca, +} = \max (|σ_{1, +} - σ_{2, +}|; |σ_{2, +}|; |σ_{1, +}|) bzw .

σ_{v, Tresca, +} = \max (\sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{xy, +}}^{2}}; |σ_{2, +}|; |σ_{1, +}|)

位于面的“+”表面上的等效Tresca应力 σ_v,Tresca,+

σ_{v, Tresca, -} = \max (|σ_{1, -} - σ_{2, -}|; |σ_{2, -}|; |σ_{1, -}|) bzw .

σ_{v, Tresca, -} = \max (\sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{xy, -}}^{2}}; |σ_{2, -}|; |σ_{1, -}|)

位于面的“-”表面上的等效Tresca应力 σ_v,Tresca,-

σ_{v, Tresca, m} = \max (|σ_{1, m} - σ_{2, m}|; |σ_{2, m}|; |σ_{1, m}|) bzw .

σ_{v, Tresca, m} = \max (\sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{xy, m}}^{2}}; |σ_{2, m}|; |σ_{1, m}|)

根据Tresca屈服准则得到的等效膜应力 σ_v,Tresca,m

Rankine

Rankine准则也被称为最大主应力准则，当材料中一点的主应力达到单向应力状态的极限值，材料即发生屈服破坏。

平面应力状态下的 Rankine 等效应力与基本应力、主应力之间的关系如下：

σ_{v, Rankine, Max} = \max (σ_{v, Rankine, +}; σ_{v, Rankine, -})

最大等效Rankine应力σ_{v,Rankine,max}

σ_{v, Rankine, +} = \frac{1}{2} |σ_{x, +} + σ_{y, +}| + \frac{1}{2} \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{xy, +}}^{2}}

面的“+”表面的等效Rankine应力 σ_v,Rankine,+

σ_{v, Rankine, -} = \frac{1}{2} |σ_{x, -} + σ_{y, -}| + \frac{1}{2} \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{xy, -}}^{2}}

面的“-”表面的等效Rankine应力 σ_v,Rankine,-

σ_{v, Rankine, m} = \frac{1}{2} |σ_{x, m} + σ_{y, m}| + \frac{1}{2} \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{xy, m}}^{2}}

根据Rankine准则得到的等效膜应力 σ_{v, Rankine,m}

Bach

Bach准则也被称为最大主应变准则，当材料中一点的主应变达到单向应力状态的极限值，即发生屈服破坏。 Bach准则类似于 Rankine 准则。所不同的是Bach准则使用的是主应变，而Rankine准则使用的是主应力。

平面应力状态下的Bach等效应力与基本应力、主应力之间的关系如下：

σ_{v, Bach, Max} = \max (σ_{v, Bach, +}; σ_{v, Bach, -})

最大等效Bach应力 σ_v,Bach,max

σ_{v, Bach, +} = \max (\frac{1 - ν}{2} |σ_{x, +} + σ_{y, +}| + \frac{1 + ν}{2} \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{xy, +}}^{2}}; ν |σ_{x, +} + σ_{y, +}|)

ν

泊松比

面的“+”表面上的等效Bach应力 σ_v,Bach,+

σ_{v, Bach, -} = \max (\frac{1 - ν}{2} |σ_{x, -} + σ_{y, -}| + \frac{1 + ν}{2} \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{xy, -}}^{2}}; ν |σ_{x, -} + σ_{y, -}|)

面的“-”表面上的等效Bach应力 σ_v,Bach,-

σ_{v, Bach, m} = \max (\frac{1 - ν}{2} |σ_{x, m} + σ_{y, m}| + \frac{1 + ν}{2} \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{xy, m}}^{2}}; ν |σ_{x, m} + σ_{y, m}|)

根据Bach准则计算得到的等效膜应力 σ_v,Bach,m

上级章节

结果(按面)