Die Standard-Integrationsmethode in RFEM ist eine Gauß-Lobatto-Quadratur mit neun Integrationspunkten. Diese Voreinstellung ist für die meisten Fälle ausreichend. Um insbesondere nichtlineare Spannungs-Dehnungs-Verläufe ausreichend genau abzubilden (beispielsweise bei Stahlfaserbeton), kann es sinnvoll sein, die Anzahl an Integrationspunkten zu erhöhen. Deshalb ist es bei der Verwendung von nichtlinearem Material möglich, die Anzahl der Integrationspunkte in jeder Schicht zwischen drei und 99 Punkten benutzerdefiniert festzulegen (siehe Bild Integrationspunkte für Schichten anpassen ). Beachten Sie aber, dass eine höhere Anzahl an Integrationspunkten mit einer längeren Berechnungszeit verbunden ist.
Des Weiteren stehen drei verschiedene Integrationsmethoden zur Auswahl (siehe Bild Integrationsmethode angeben ):
- Gauß-Lobatto-Quadratur
- Simpsonregel
- Trapezregel
Diese Integrationsmethoden – auch als Quadraturformeln bezeichnet – werden nachfolgend erklärt. Im Allgemeinen kann davon ausgegangen werden, dass die Gauß-Lobatto-Quadratur bei fester Anzahl der Integrationspunkte die höchste Genauigkeit liefert, ohne den Rechenaufwand maßgeblich zu erhöhen. Nur in Sonderfällen führt die Anwendung der Trapez- oder Simpsonregel zu einem besseren Ergebnis.
Quadraturformeln
Das Ziel einer Quadraturformel ist es, eine numerische Approximation an ein Integral zu berechnen. Dafür werden in dem Integrationsgebiet Stützstellen ausgewählt und die Funktionsauswertungen an diesen Stellen gewichtet addiert. Als Beispiel für die folgenden Erklärungen wird die Berechnung des Moments verwendet.
Dabei bezeichnet d die Höhe einer beliebigen Schicht in einer mehrschichtigen Fläche. Es wird dann versucht, das Integral wie folgt anzunähern:
Hierfür werden n Stützstellen −d/2 ≤ z1 < z2 < . . . < zn ≤ d/2 über die Höhe der Schicht sowie skalare Gewichte ω1, . . . , ωn benötigt, die spezifisch für die jeweilige Quadraturformel sind.
In RFEM wird immer eine ungerade Anzahl n = 2k + 1 an Stützstellen verwendet und mindestens die Schichtoberseite, -mitte und -unterseite als Integrationspunkte gewählt. Es ergibt sich also z1 = −d/2, zk = 0 und zn = d/2. Das ist nötig, damit die Spannungswerte an diesen Stellen exakt berechnet und anschließend im Programm angezeigt werden können. Sollte eine gerade Stützstellenanzahl vorgegeben werden, so wird mit der nächsthöheren ungeraden Zahl gerechnet.
Der Genauigkeitsgrad einer Quadraturformel wird in ihrer Ordnung p angegeben. Dies ist der höchste Grad eines Polynoms, welches exakt integriert wird.
Trapezregel
Ein einfaches Beispiel für eine Quadraturformel ist die Trapezregel. Hierbei werden die beiden äußeren Ränder des Integrationsgebiets als Stützstellen gewählt, also z1 = −d/2 und z2 = d/2. Die Trapezregel ist von erster Ordnung, da lineare Funktionen exakt integriert werden, quadratische Funktionen aber nicht.
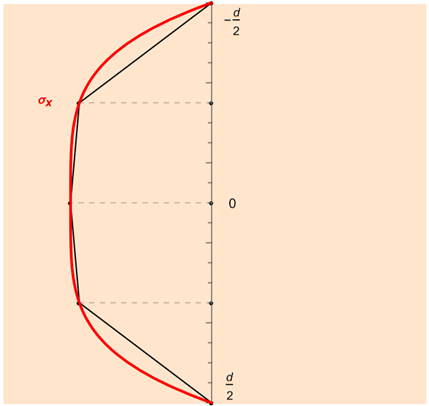
Bei der in RFEM verwendeten Variante der summierten Trapezregel wird das Integrationsintervall bei einer Wahl von n Integrationspunkten äquidistant in n−1 Teilintervalle zerlegt und auf diese jeweils die Trapezregel angewendet.
In der folgenden Abbildung ist die summierte Trapezregel für fünf Integrationspunkte beispielhaft dargestellt.
Simpsonregel
Die Simpsonregel ist eine Quadraturformel von dritter Ordnung, die drei Integrationspunkte verwendet – zwei an den Rändern und einen in der Mitte des Integrationsgebiets. Die Gewichte sind so gewählt, dass die Näherungslösung dem Integral über einer Parabel entspricht, welche durch diese drei Punkte verläuft. Mit z1 = −d/2, z2 = 0 und z3 = d/2 ergibt sich die Form
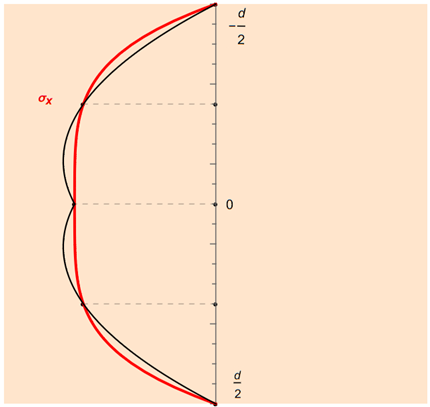
Auch hier verwendet RFEM eine summierte Quadratur. Bei einer ungeraden Anzahl n an Stützstellen ergeben sich (n−1)/2 gleich lange Teilintervalle, auf die die Simpsonregel angewendet werden kann. Die Abbildung zeigt dies wieder beispielhaft für fünf Integrationspunkte.
Gauß-Lobatto-Quadratur
Bei der Gauß-Lobatto-Quadratur werden immer die beiden Randpunkte z1 = −d/2 und zn = d/2 als Stützstellen vorgegeben und alle weiteren Integrationspunkte so gewählt, dass eine möglichst hohe Ordnung erreicht wird. Diese liegt bei p = 2n − 3. Für n = 3 stimmt die Gauß-Lobatto-Quadratur mit der Simpsonregel überein; für n = 5 ergibt sich beispielsweise: