Domyślną metodą całkowania w programie RFEM jest kwadratura Gaussa-Lobatto z dziewięcioma punktami całkowania. To domyślne ustawienie jest wystarczające w większości przypadków. Aby z wystarczającą dokładnością odwzorować nieliniowe wykresy naprężenie-odkształcenie (na przykład w przypadku betonu zbrojonego włóknami stalowymi), korzystne może być zwiększenie liczby punktów całkowania. Dlatego w przypadku stosowania materiału nieliniowego można dostosować liczbę punktów integracji w każdej warstwie od trzech do 99 punktów (patrz ilustracja Dostosowywanie punktów całkowania dla warstw ). Należy jednak pamiętać, że większa liczba punktów całkowania wydłuża czas obliczeń.
Ponadto do wyboru dostępne są trzy różne metody integracji (patrz ilustracja Określanie metody całkowania ):
- kwadratura Gaussa-Lobatto
- metoda Simpsona
- metoda trapezów
Te metody całkowania, znane również jako równania kwadraturowe, wyjaśniono poniżej. Ogólnie można założyć, że kwadratura Gaussa-Lobatto ze stałą liczbą punktów całkowania zapewnia najwyższą dokładność bez znacznego zwiększania nakładu pracy obliczeniowej. Metoda trapezów lub reguła Simpsona' prowadzi do lepszego wyniku tylko w szczególnych przypadkach.
Wzory kwadraturowe
Celem wzoru kwadraturowego jest obliczenie numerycznego przybliżenia do całki. W tym celu w obszarze całkowania wybierane są punkty podparcia, w których dodawane są wartości funkcji ważonych. Obliczanie momentu posłużyło jako przykład w poniższych wyjaśnieniach.
d jest wysokością dowolnej warstwy w powierzchni wielowarstwowej. Program próbuje następnie przybliżyć całkę w następujący sposób:
W tym celu należy zastosować n punktów rastra −d/2 ≤ z1 < z2 < . . . < zn ≤ d/2 na wysokości warstwy oraz wagi skalarne ω1, . . . , ωn są specyficzne dla danego wzoru kwadraturowego.
Program RFEM zawsze używa nieparzystej liczby punktów rastra n = 2k + 1, a jako punkty całkowania wybierane są co najmniej góra, środek i dół warstwy. Zatem z1 = −d/2, zk = 0 i zn = d/2. Jest to konieczne, aby wartości naprężeń w tych miejscach można było dokładnie obliczyć, a następnie wyświetlić w programie. W przypadku ustawienia parzystej liczby punktów rastra do obliczeń zostaje zastosowana następna co do wielkości nieparzysta liczba.
Stopień dokładności równania kwadraturowego jest podany w kolejności p. Jest to najwyższy stopień wielomianu, który jest dokładnie całkowany.
metoda trapezów
Prostym przykładem wzoru kwadraturowego jest reguła trapezów. W tym przypadku jako miejsca podparcia wybierane są dwie zewnętrzne krawędzie obszaru całkowania; oznacza to, że z1 = −d/2 oraz z2 = d/2. Reguła trapezów jest regułą pierwszego rzędu, ponieważ całkuje się dokładnie funkcje liniowe, ale nie funkcje kwadratowe.
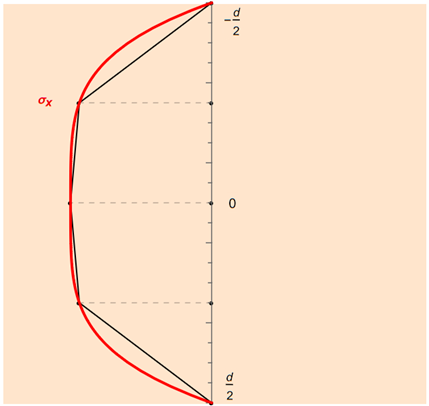
W przypadku wariantu kumulacyjnej reguły trapezów stosowanej w programie RFEM, po wybraniu n punktów całkowania, przedział całkowania jest dzielony na n − 1 przedziałów częściowych, a do każdego z nich zostaje zastosowana reguła trapezów.
Poniższy rysunek przedstawia przykład zsumowanej reguły trapezów dla pięciu punktów całkowania.
metoda Simpsona
Reguła Simpsona' jest równaniem kwadraturowym trzeciego rzędu wykorzystującym trzy punkty całkowania – dwa na krawędziach i jeden w środku obszaru całkowania. Wagi są dobrane w taki sposób, aby przybliżone rozwiązanie odpowiadało całce po paraboli przebiegającej przez te trzy punkty. Jeżeli z1 = −d/2, z2 = 0 i z3 = d/2, otrzymujemy kształt:
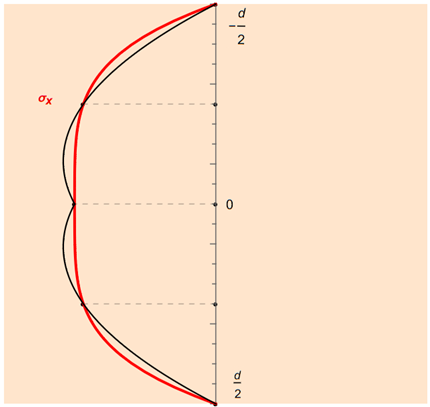
Program RFEM wykorzystuje tu również kwadraturę złożoną. Jeżeli istnieje nieparzysta liczba n punktów podparcia, uzyskuje się (n − 1)/2 jednakowo długie przedziały częściowe, do których można zastosować regułę Simpsona's. Rysunek pokazuje przykład dla pięciu punktów całkowania.
kwadratura Gaussa-Lobatto
W kwadraturze Gaussa-Lobatto jako punkty podparcia zawsze podaje się dwa punkty graniczne z1 = −d/2 i zn = d/2, a wszystkie pozostałe punkty całkowania są wybierane w taki sposób, aby uzyskać najwyższy możliwy rząd. To jest p = 2n − 3. Dla n = 3, kwadratura Gaussa-Lobatto jest równoważna regule Simpsona's; dla n = 5, na przykład: