Методом интегрирования по умолчанию в программе RFEM является квадратура Гаусса-Лобатто с девятью точками интегрирования. В большинстве случаев данной настройки по умолчанию достаточно. Для отображения нелинейных диаграмм напряжения-деформации с достаточной точностью (например, у сталефибробетона) может быть полезно увеличить количество точек интегрирования. Поэтому при использовании нелинейного материала можно настроить количество точек интегрирования в каждом слое в диапазоне от трех до 99 точек (см.|изображение042051|Настройка точек интеграции для слоёв#). Пожалуйста, обратите внимание, что большее количество точек интегрирования приводит к увеличению времени вычисления.
Кроме того, для выбора доступны три различных метода интеграции (см.|изображение039558|Задание метода интеграции#):
- Квадратура Гаусса-Лобатто
- Правило Симпсона
- Трапециевидное правило
Эти методы интегрирования, также известные как квадратурные формулы, объясняются ниже. В общем случае можно предположить, что квадратура Гаусса-Лобатто с фиксированным количеством точек интегрирования обеспечивает наивысшую точность без значительного увеличения вычислительной работы. Правило трапеции или правило Симпсона' приводят к лучшему результату только в особых случаях.
Квадратурные формулы
Целью квадратурной формулы является численное приближение интеграла. Для этого выберем в области интегрирования опорные точки, и в них зададим взвешенные оценки функции. Расчет момента будет использован в качестве примера в последующих пояснениях.
d - высота любого слоя многослойной поверхности Программа затем попытается аппроксимировать интеграл следующим образом:
Для этого нужно n точек решетки −d/2 ≤ z1 < z2 < . . . < zn ≤ d/2 от высоты слоя, а также скалярные веса ω1, . . . , ωn специфичные для соответствующей квадратурной формулы.
RFEM всегда использует нечетное количество n = 2k + 1 точек решетки, а в качестве точек интегрирования выбирается, как минимум, верхняя, средняя и нижняя часть слоя. Таким образом, мы получим z1 = −d/2 , zk = 0 и zn = d/2. Это необходимо для того, чтобы значения напряжений в данных местах можно было точно рассчитать и затем отобразить в программе. При установке четного количества точек решетки, для расчета используется следующий по величине нечетный номер.
Степень точности квадратурной формулы дается в ее порядке p. Это высшая степень точно интегрированного полинома.
Трапециевидное правило
Простым примером квадратурной формулы является правило трапеций. В качестве мест расположения опор выберем два внешних края области интегрирования, то есть z1 = -d/2 и z2 = d/2. Правило трапеций имеет первый порядок, поскольку линейные функции интегрируются точно, а квадратичные - нет.
В случае варианта кумулятивного правила трапеции, используемого в RFEM, при выборе n точек интегрирования будет интервал интегрирования эквидистантно разделен на n - 1 частичных интервалов, и к каждому из них будет применяться правило трапеции.
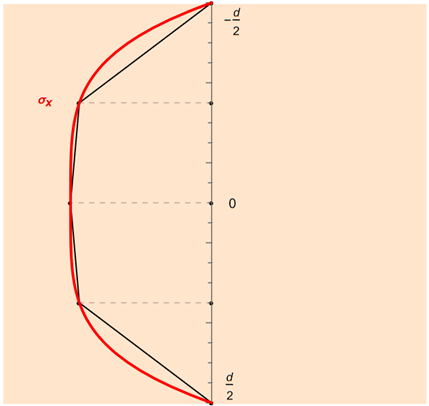
На следующем рисунке показан пример суммированного правила трапеции для пяти точек интеграции.
Правило Симпсона
Правило Симпсона' - это квадратурная формула третьего порядка, в которой используются три точки интегрирования - две на краях и одна в центре области интегрирования. Веса выбираются таким образом, чтобы приближенное решение соответствовало интегралу по параболе, которая проходит через эти три точки. С z1 = -d/2 , z2 = 0 и z3 = d/2, мы получаем форму:
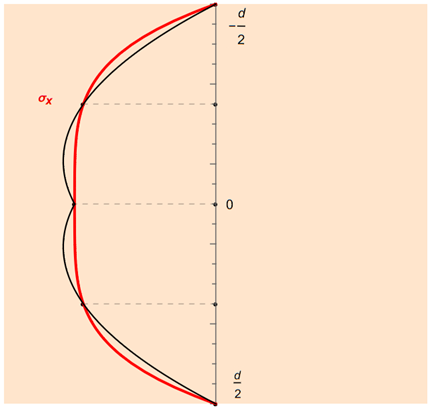
Здесь программа RFEM также применяет каркасную квадратуру. При нечетном количестве n опорных точек получается (n - 1)/2 частичных интервалов одинаковой длины, к которым можно применить правило Симпсона. На рисунке это снова показано для примера для пяти точек интеграции.
Квадратура Гаусса-Лобатто
В квадратуре Гаусса-Лобатто две граничные точки z1 = -d/2 и zn = d/2 всегда задаются как опорные, а все остальные точки интегрирования выбираются таким образом, чтобы можно было достичь максимально возможного порядка. Это p = 2n - 3, При n = 3 квадратура Гаусса-Лобатто эквивалентна правилу Симпсона; для n = 5, например: