La méthode d’intégration par défaut dans RFEM est une quadrature de Gauss-Lobatto avec neuf points d’intégration. Ce paramètre par défaut est suffisant dans la plupart des cas. Afin de représenter les diagrammes contrainte-déformation non linéaires avec une précision suffisante (par exemple, dans le cas du béton fibré), augmenter le nombre de points d’intégration peut être utile. Par conséquent, lors de l’utilisation d’un matériau non linéaire, il est possible de personnaliser le nombre de points d’intégration dans chaque couche entre trois et 99 points (voir l’image Ajustement des points d’intégration pour les couches ). Veuillez cependant noter qu’un nombre plus élevé de points d’intégration allonge le temps de calcul.
De plus, trois méthodes d’intégration différentes sont disponibles (voir l’image Spécification de la méthode d’intégration ) :
- Quadrature de Gauss-Lobatto
- Méthode de Simpson
- Méthode des trapèzes
Ces méthodes d’intégration, également appelées formules quadratiques, sont expliquées ci-dessous. En général, on peut supposer que la quadrature de Gauss-Lobatto avec un nombre fixe de points d’intégration fournit la plus grande précision sans augmenter considérablement l’effort de calcul. La méthode des trapézes ou de Simpson ne permet d’obtenir un meilleur résultat que dans des cas particuliers.
Formules de quadrature
Le but d’une formule de quadrature est de calculer une approximation numérique d’une intégrale. Pour ce faire, des points d’appui sont sélectionnés dans le domaine d’intégration et les évaluations de fonction pondérées y sont ajoutées. Le calcul d’un moment est utilisé comme exemple pour les explications suivantes.
Ici, « d » est la hauteur d’une couche dans une surface multicouche. Le logiciel essaie alors l’approximation de l’intégrale comme suit :
Pour cela, « n » points de grille −d/2 ≤ z1 < z2 < . . . < zn ≤ d/2 sur la hauteur de la couche, ainsi que les poids scalaires ω1, . . . , ωn sont nécessaires et spécifiques à la formule de quadrature correspondante.
RFEM utilise toujours un nombre impair n = 2k + 1 de points de grille et au moins le haut, le milieu et le bas de la couche sont sélectionnés comme points d’intégration. Il en résulte donc que z1 = -d/2, zk = 0 et zn = d/2. C’est nécessaire pour que les valeurs de contrainte à ces positions puissent être calculées précisément et affichées dans le logiciel. Si vous définissez un nombre pair de points de grille, le nombre impair le plus élevé est utilisé pour le calcul.
Le degré de précision d’une formule de quadrature est donné dans son ordre « p ». Il s’agit du degré le plus élevé d’un polynôme, qui est exactement intégré.
Méthode des trapèzes
La méthode des trapèzes est un exemple simple de formule de quadrature. Dans ce cas, les deux bords extérieurs du domaine d’intégration sont sélectionnés comme points de grille, c’est-à-dire z1 = -d/2 et z2 = d/2. La méthode des trapèzes est du premier ordre, car les fonctions linéaires sont intégrées exactement, mais les fonctions quadratiques ne le sont pas.
Dans le cas de la variante de la méthode des trapèze additionnée utilisée dans RFEM, si vous sélectionnez « n » points d’intégration, l’intervalle d’intégration est divisé de manière équidistante en n - 1 intervalles partiels et la méthode des trapèzes est appliquée à chacun.
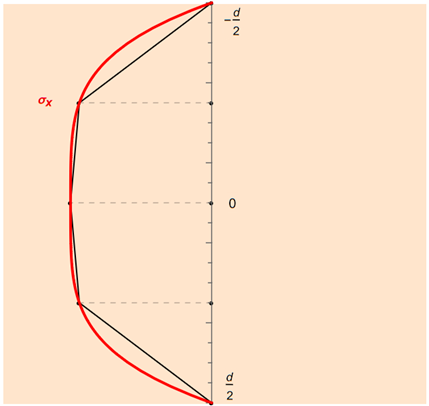
La figure suivante montre un exemple de la méthode des trapèzes additionnée pour cinq points d’intégration.
Méthode de Simpson
La méthode de Simpson est une formule de quadrature du troisième ordre qui utilise trois points d’intégration, deux sur les bords et un au centre de la zone d’intégration. Les poids sont sélectionnés de sorte que la solution approximative corresponde à l’intégrale sur une parabole traversant ces trois points. Avec z1 = -d/2, z2 = 0 et z3 = d/2, on obtient :
RFEM utilise également une quadrature composée. Si le nombre « n » impair de points de grille est obtenu, (n - 1)/2 intervalles partiels de même longueur auxquels la méthode de Simpson peut être appliquée. La figure le montre à nouveau à titre d’exemple pour les cinq points d’intégration.
Quadrature de Gauss-Lobatto
Dans la quadrature de Gauss-Lobatto, les deux points de contour z1 = -d/2 et zn = d/2 sont toujours définis comme des points de grille et tous les autres points d’intégration sont sélectionnés de manière à obtenir le plus haut ordre possible. Cela nous donne p = 2n − 3. Pour n = 3, la quadrature de Gauss-Lobatto est équivalente à la méthode de Simpson. Pour n = 5, par exemple :