Back to Online Manuals

10319x

000076

Dipl.-Ing. Frank Faulstich

2023-12-14

Select Manual

Overview

Graphical User Interface and Settings

Dlubal Center

Model Base Data

Structure

Imperfections

Load Cases and Combinations

Load Wizards

Loads

Result Objects

Costs and Emissions

Calculation

Results

Guide Objects

Digital Twins

Program Functions

Result Evaluation

Printout Reports

Drawing Sheets

Nonlinear Material Behavior

Material Models

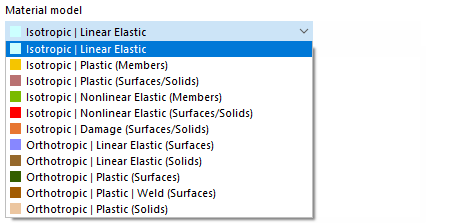
If the analysis add-on Nonlinear material behavior is activated in the Model base data (license required), further options are available in the list of material models in addition to the Isotropic | Linear elastic and Orthotropic | Linear elastic material models.

Material Models for Nonlinear Material Behavior Add-on

Calculation Method

When using a nonlinear material model, an iterative calculation is always performed. Depending on the material model, a different relation between stresses and strains is defined.

The stiffness of the finite elements is adjusted repeatedly during the iterations until the stress-strain relation is fulfilled. The adjustment is always applied to an entire surface or solid element. Therefore, when evaluating the stresses, the smoothing type Constant in finite elements should always be used.

Result Smoothing

Plastic and Nonlinear Elastic Material Models

Some material models are labeled "plastic" in RFEM, others "nonlinear elastic". If a component with a nonlinear elastic material is unloaded again, the strain returns along the same path. After complete load relief, no strain remains.

Stress-Strain Diagram for Nonlinear Elastic

When unloading a component with a plastic material model, a strain remains after complete load relief.

Stress-Strain Diagram for Plastic

Loading and unloading can be simulated with the add-on Construction Stages Analysis.

Tip

For more information on nonlinear elastic material models, see the technical article Yield laws in the material model Isotropic nonlinear elastic.

Surface Internal Forces

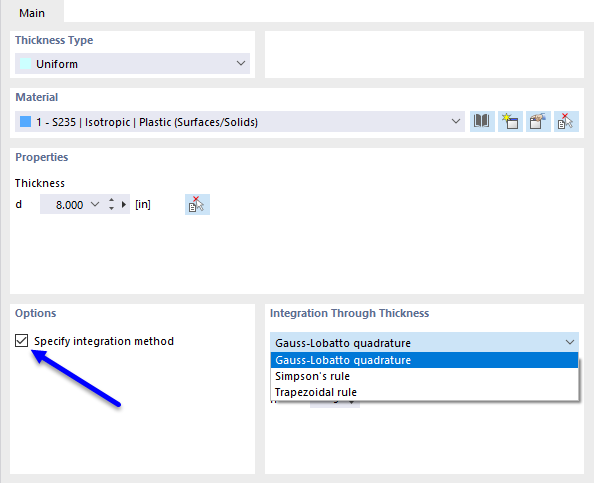
The internal forces in slabs with nonlinear material result from the numerical integration of the stresses over the plate thickness. To define the integration method for the thickness, check the option Specify integration method in the 'Edit thickness' dialog. This provides the following integration methods for selection:

Gauss-Lobatto quadrature
Simpson's rule
Trapezoidal rule

Defining Integration Method for Surface Thickness

Furthermore, you can specify the 'number of integration points' over the plate thickness from 3 to 99.

Tip

Theoretical background on the individual integration methods can be found in the manual Multilayer Surfaces.

Isotropic | Plastic (Members)

If you select the entry Isotropic | Plastic (Members) in the 'Material model' drop-down list, the tab for entering the nonlinear material parameters becomes active.

Activating Nonlinear Material Model

Defining Nonlinear Material Parameters

In this tab, you define the stress-strain diagram. The following options are available for selection:

Standard
Bilinear
Diagram

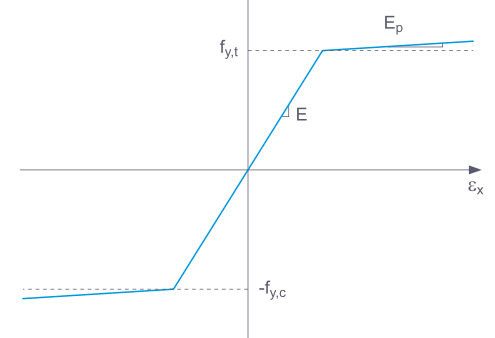
If Standard is selected, RFEM uses a bilinear material model. The values for the modulus of elasticity E and the yield strength f_y are taken from the material library. For numerical reasons, the branch does not run exactly horizontally, but has a small slope E_p.

If you want to change the values for the yield strength and the modulus of elasticity, activate the User-defined material check box in the 'Basic' tab.

Activating User-Defined Material

With the bilinear definition, you can also enter the value for E_p.

You define more complex relations between stress and strain by means of a stress-strain diagram. If you select this option, the 'Stress-strain diagram' tab is displayed.

Entering a user-defined stress-strain diagram

Entering User-Defined Stress-Strain Diagram

Define a point for the stress-strain relation in each row. How the diagram should continue after the last definition point can be selected in the 'Diagram end' list below the diagram:

Distribution after the last definition point

Distribution After Last Definition Point

With 'Failure', the stress jumps back to zero after the last definition point (for example, when the material tears). 'Yielding' means that the stress remains constant with increasing strain. 'Continuous' means that the curve continues with the slope of the last section.

Info

In this material model, the stress-strain diagram refers to the longitudinal stress σ_x. Different yield strengths for tension and compression cannot be taken into account with this material model.

Isotropic | Plastic (Surfaces/Solids)

If you select the entry Isotropic | Plastic (Surfaces/Solids) in the 'Material model' drop-down list, the tab for entering the nonlinear material parameters becomes active.

Selecting Plastic Material Model

First, select the 'stress failure hypothesis'. The following hypotheses are available:

von Mises (distortion energy hypothesis)
Tresca (shear stress hypothesis)
Drucker-Prager
Mohr-Coulomb

Defining Stress Failure Hypothesis

If you select von Mises, the following stresses are used in the stress-strain diagram:

Surfaces

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Equivalent Stress from Basic Stresses According to von Mises

Solids

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Equivalent Stress σ_v,Mises from Basic Stresses

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Equivalent Stress σ_v,Mises from Principal Stresses

According to the Tresca hypothesis, these stresses are used:

Surfaces

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Equivalent Stress According to Tresca

Solids

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Equivalent Stress σ_v,Tresca

According to the Drucker-Prager hypothesis, this stress is used for surfaces and solids:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Limit stress for compression
σ_t	Limit stress for tension

Yield Criterion According to Drucker-Prager

According to the Mohr-Coulomb hypothesis, the following stress is used for surfaces and solids:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr – Coulomb

Isotropic | Nonlinear Elastic (Members)

The mode of operation largely corresponds to that of the Plastic (Members) material model. However, in contrast to this model, no plastic strain remains after load relief.

Isotropic | Nonlinear Elastic (Surfaces/Solids)

The mode of operation largely corresponds to that of the Plastic (Surfaces/Solids) material model. However, in contrast to this model, no plastic strain remains after load relief.

Isotropic | Damage (Surfaces/Solids)

In contrast to other material models, the stress-strain diagram for this material model is not antisymmetric about the origin. Thus, this material model can be used, for example, to represent the behavior of steel fiber reinforced concrete. For detailed information on modeling steel fiber reinforced concrete, see the technical article Material properties of steel fiber reinforced concrete.

Material Model "Isotropic | Damage"

The isotropic stiffness is reduced by a scalar damage parameter. This damage parameter is determined by the course of the stress defined in the diagram. The direction of the principal stresses is not taken into account; rather, the damage occurs in the direction of the equivalent strain, which also covers the third direction perpendicular to the plane. The tension and compression areas of the stress tensor are treated separately. Different damage parameters apply in each case.

The 'reference element size' controls how the strain in the crack area is scaled to the length of the element. With the preset value of zero, no scaling is performed. This represents the material behavior of steel fiber reinforced concrete realistically.

Tip

Theoretical background on the material model 'Isotropic Damage' can be found in the technical article Nonlinear damage material model.

Orthotropic | Anisotropic Damage

Timber materials exhibit direction-dependent properties. The anisotropic principal directions run in the grain direction, radially, and tangentially. In the Orthotropic | Anisotropic Damage tab, you can define the nonlinear properties.

Material Model "Orthotropic | Anisotropic Damage"

This material model implements the damage model by Sandhaas [2] with eight failure criteria for timber. Timber behaves quasi-brittle under tension and shear and ductile under compression, and it fails in planes defined by the grain direction. The model according to [2] describes eight separate failure criteria (one per quadrant of the stress space) that govern nine stiffness reduction factors.

The local axis x runs in the grain direction, axis y radially, and axis z tangentially. Each criterion is a stress function F that reaches the value 1 at the onset of damage. Four of them are simple maximum stress criteria. The four criteria for tensile stress perpendicular to the grain and shear are elliptical: splitting in a plane can be triggered by tension perpendicular to it, by shear along the plane, or by any combination thereof.

Specify the limit strengths of the material as well as the tensile fracture energy and the shear fracture energy for each direction.

Info

In contrast to the material model Orthotropic | Plastic, the forces are not redistributed, but decoupled by the failure of the grain plane. This allows the splitting behavior of timber to be represented. The deformations are usually smaller.

Deformations for the Orthotropic | Plastic (left) and Orthotropic | Anisotropic damage (right) material model

Deformations for Material Model Orthotropic | Plastic (Left) and Orthotropic | Anisotropic Damage (Right)

Orthotropic | Plastic (Surfaces) / Plastic (Solids)

The material model according to Tsai-Wu combines plastic and orthotropic properties. This allows special modeling of materials with anisotropic characteristics such as fiber-reinforced plastics or timber.

When the material yields, the stresses remain constant. A redistribution takes place depending on the stiffnesses present in the individual directions.

Material Model "Orthotropic | Plastic (Surfaces)"

Material Model "Orthotropic | Plastic (Solid)"

The elastic range corresponds to the material model Linear elastic (Solids). The following yield condition according to Tsai-Wu applies to the plastic range:

Surfaces

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, State of Plane Stress

Solids

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, Spatial State of Stress

All strengths must be defined as positive.

The yield condition can be imagined as an elliptical surface in the six-dimensional stress space. If one of the three stress components is assumed to be a constant value, the surface can be projected onto a three-dimensional stress space.

If the value for f_y(σ) according to equation Tsai-Wu, state of plane stress is less than 1, the stresses are in the elastic range. The plastic range is reached as soon as f_y(σ) = 1. Values greater than 1 are not permitted. The model behaves in an ideally plastic manner, that is, no stiffening takes place.

Orthotropic | Plastic | Weld (Surfaces)

This material model is used in analyses with the Steel Joints add-on in order to represent the behavior of welds in accordance with the standards. In the substitute surface, only stresses arise that correspond to the stress components σ_⊥, τ_⊥, and τ_|| of the weld. In the other stress directions, the stiffness of the substitute surface tends toward zero.

Material Model "Orthotropic | Plastic | Weld (Surfaces)"

In the 'Orthotropic | Plastic | Weld (Surfaces)' tab, you can define the parameters for taking into account the plastic material hardening of welds, for example the limit values f_ekv and f_x for the stress check according to the "directional method" according to EN 1993-1-8 [1] for welds, modified by a plastic component (see also the technical article Design of fillet welds).

Concrete

For the 'Concrete' material type, the nonlinear material models Anisotropic | Damage and Isotropic | Damage (Surfaces/Solids) are available for selection.

Material Models for Concrete

These material models are described in the chapter Anisotropic | Damage of the Concrete manual or above in the section Damage (Surfaces/Solids).

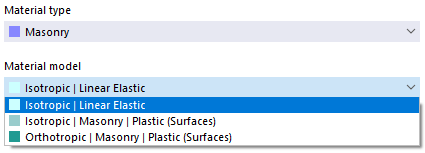
Masonry

If the design add-on Masonry Design is activated in the Model base data (license required), the nonlinear material models Isotropic | Masonry | Plastic (Surfaces) and Orthotropic | Masonry | Plastic (Surfaces) are available for the 'Masonry' material type.

Material Models for Masonry

The two material models are described in the chapter Materials of the Masonry Design manual.

Fabric

The material library contains two series for the 'Fabric' material type:

Glass-PTFE: glass fabric coated with polytetrafluoroethylene (PTFE)
PES-PVC: polyester fabric coated with polyvinyl chloride (PVC)

Info

For films such as ETFE, the 'Layer' material type is provided.

For fabric materials, in addition to the orthotropic linear material model, the nonlinear material model Orthotropic | Fabric | Nonlinear elastic (Surfaces) is available.

Material Models for Fabric

This material model enables a realistic representation of the orthotropic behavior of prestressed fabric membranes in which the stiffnesses in warp and weft directions are different. It describes the fabric by means of a representative volume element (RVE) of its microstructure. By taking the fabric geometry into account, the model captures the associated Poisson's ratio effect for all force states in the membrane. Since the load-dependent stiffness development of the fabric is also taken into account, an accurate analysis of membrane structures is possible.

The properties of fabrics are determined in biaxial tests, from which the moduli of elasticity E_x and E_y as well as the shear modulus G_xy result. However, the coupling between warp and weft directions arises from the geometry of the threads: under load, the waviness (ondulation) of the threads changes in both directions. This effect is referred to in English as crimp interchange.

The material model therefore derives the material response from a unit cell of the fabric structure. This unit cell also captures its own geometric nonlinearity. Poisson's ratios are not used in this model. The coupling of the two directions is controlled by the parameter R.

As with all nonlinear elastic material models, the strain returns along the same path when the load is relieved. The calculation is iterative.

Material Model "Orthotropic | Fabric | Nonlinear Elastic (Surfaces)"

In the 'Fabric structures' list, select the manufacturing method of the fabric. Two options are available:

Plain weave
Panama weave

Specify the modulus of elasticity in the x-direction (warp) and in the y-direction (weft). Since the shear moduli G_yz and G_xz are always zero for fabric, only the input field G_xy is offered for the Poisson's ratio in the fabric plane. This shear modulus may also be zero.

The factor R describes the ratio of height to length of the representative volume element (RVE). The value must be between 0 and 1.

If necessary, adjust the coefficients of thermal expansion of the fabric α_x in the warp direction and α_y in the weft direction. They may also be zero.

In the 'Material properties' tab, the properties of a fabric are specified as is customary in the membrane industry. The x-direction corresponds to the warp direction, the y-direction to the weft direction.

References

European Committee for Standardization. (2010). Eurocode 3: Design of Steel Structures – Part 1-8: Design of Joints. Brussels: CEN.
Sandhaas, C., Mechanical Behaviour of Timber Joints with Slotted-in Steel Plates. Dissertation, TU Delft, 2012.

Parent Chapter