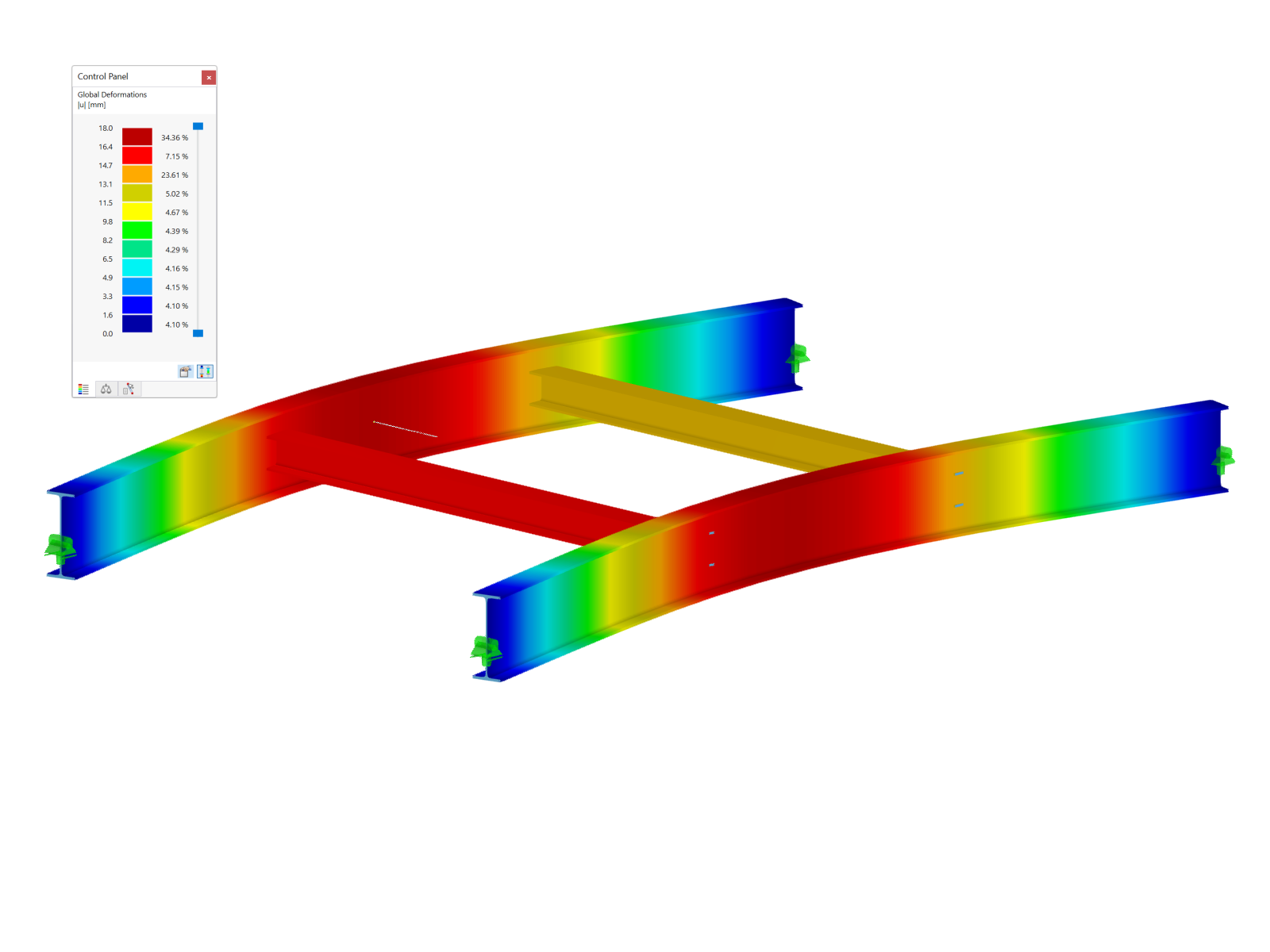
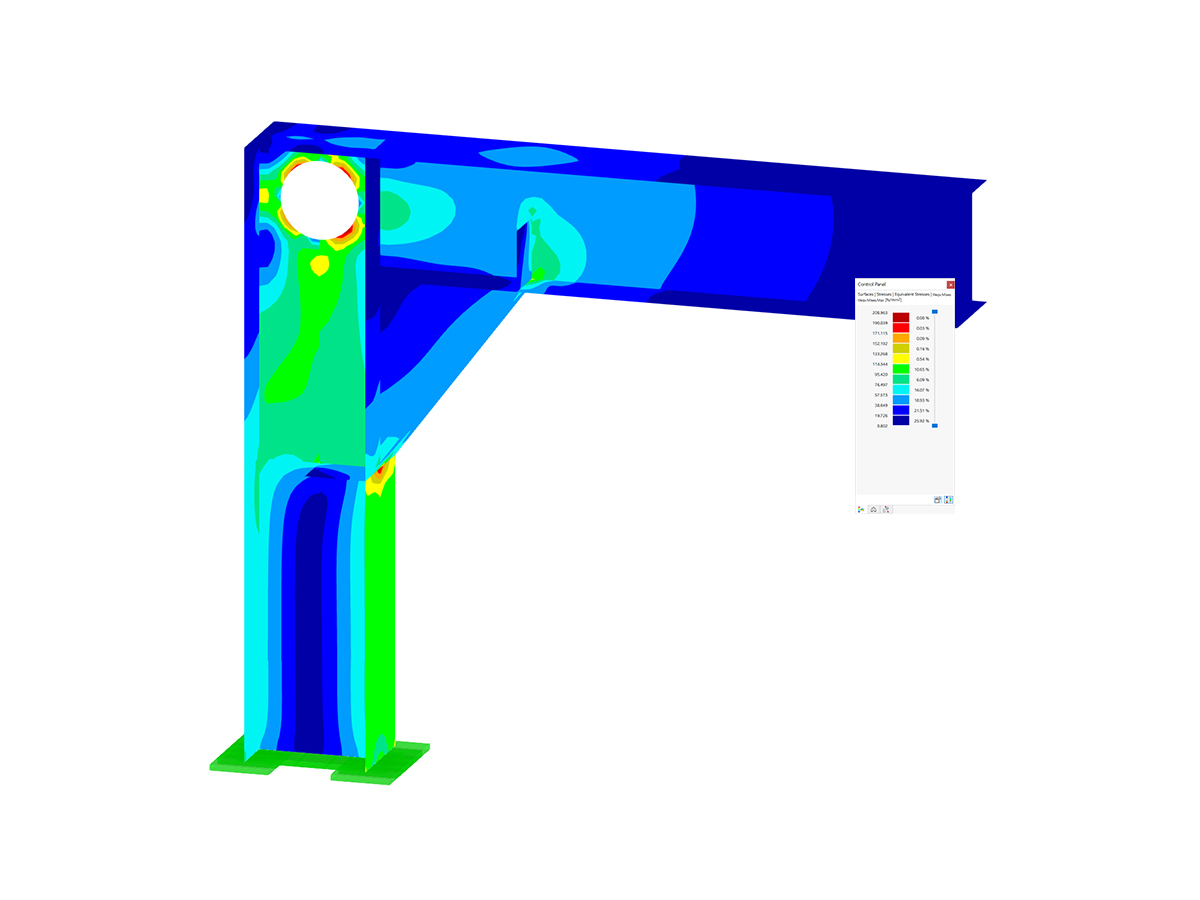
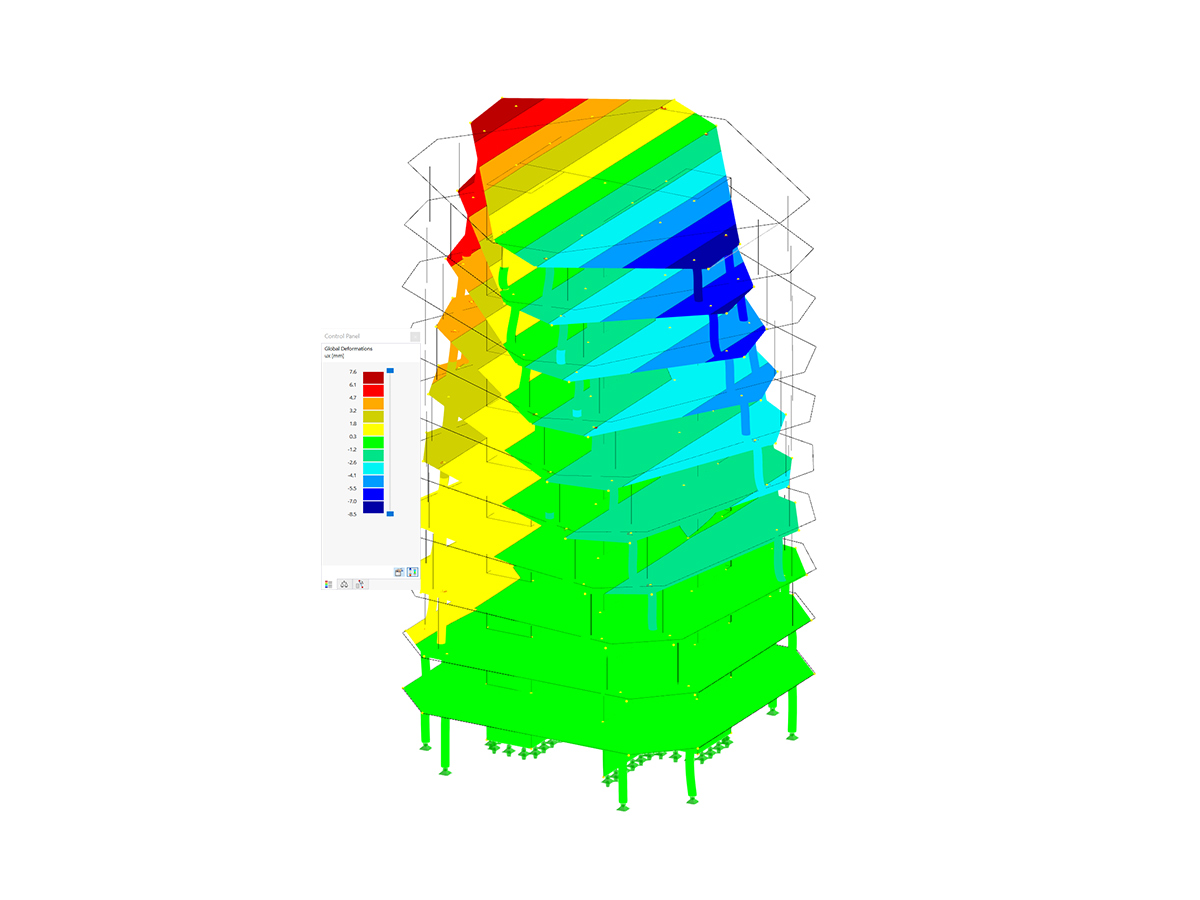
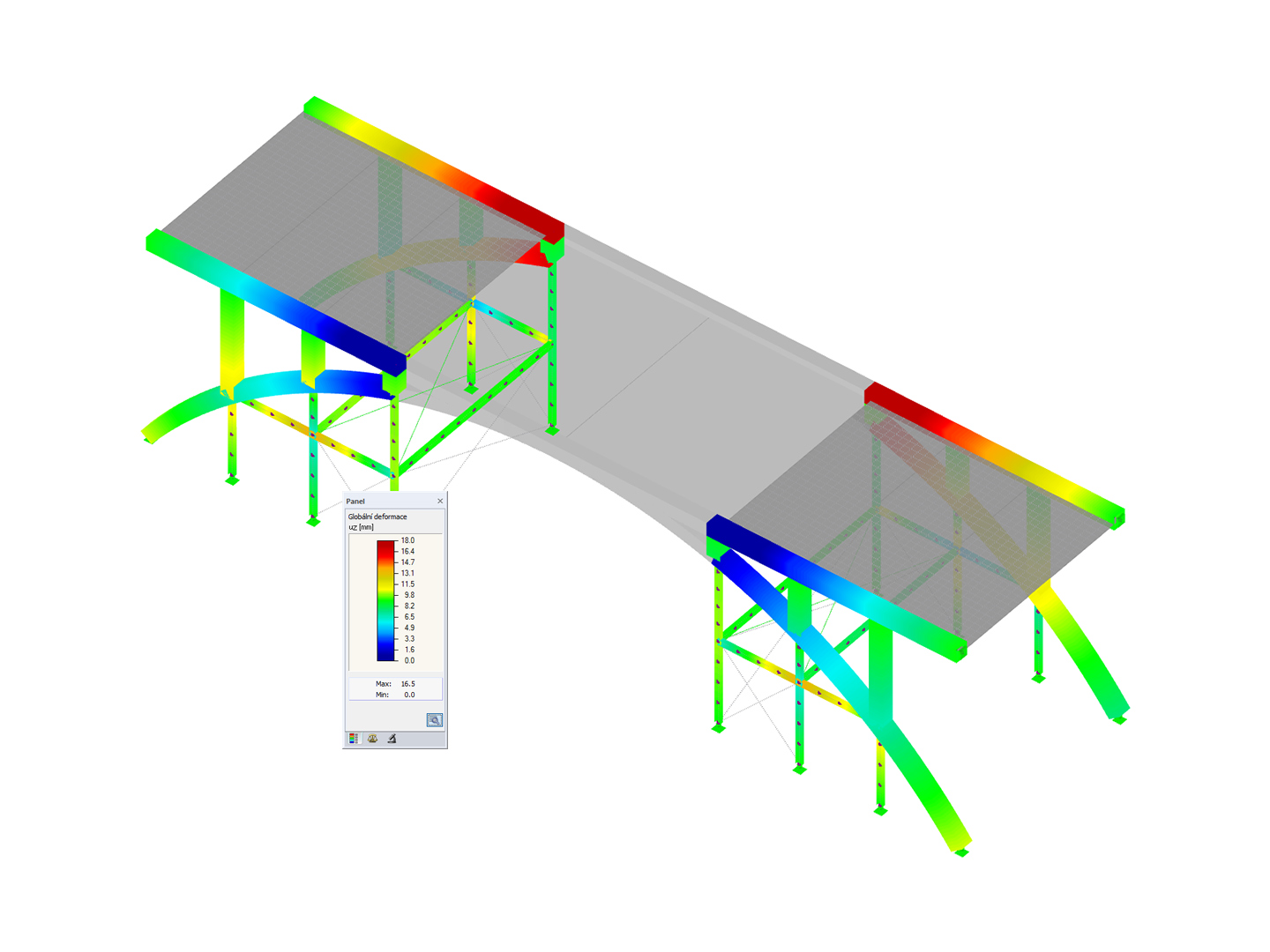
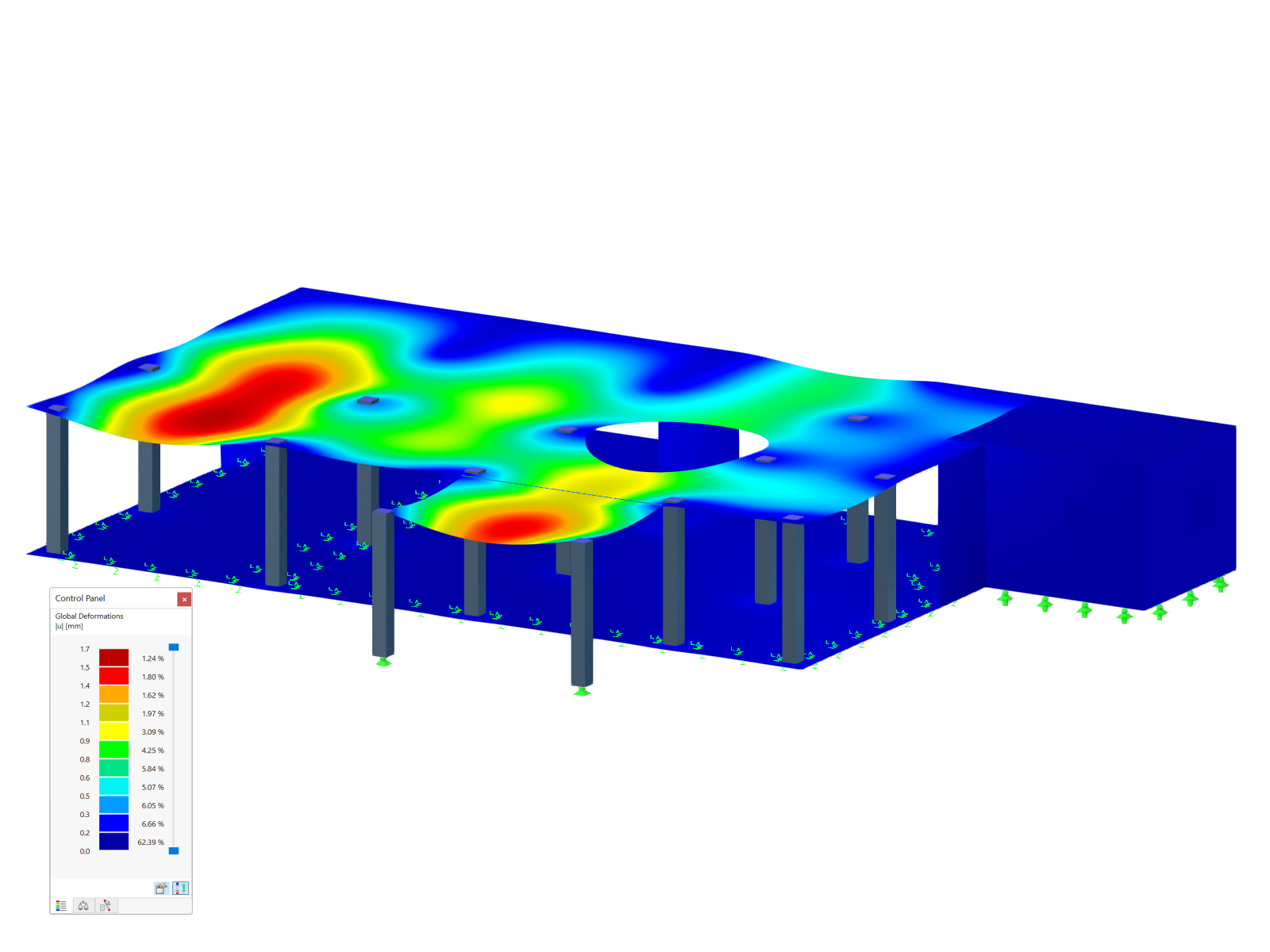
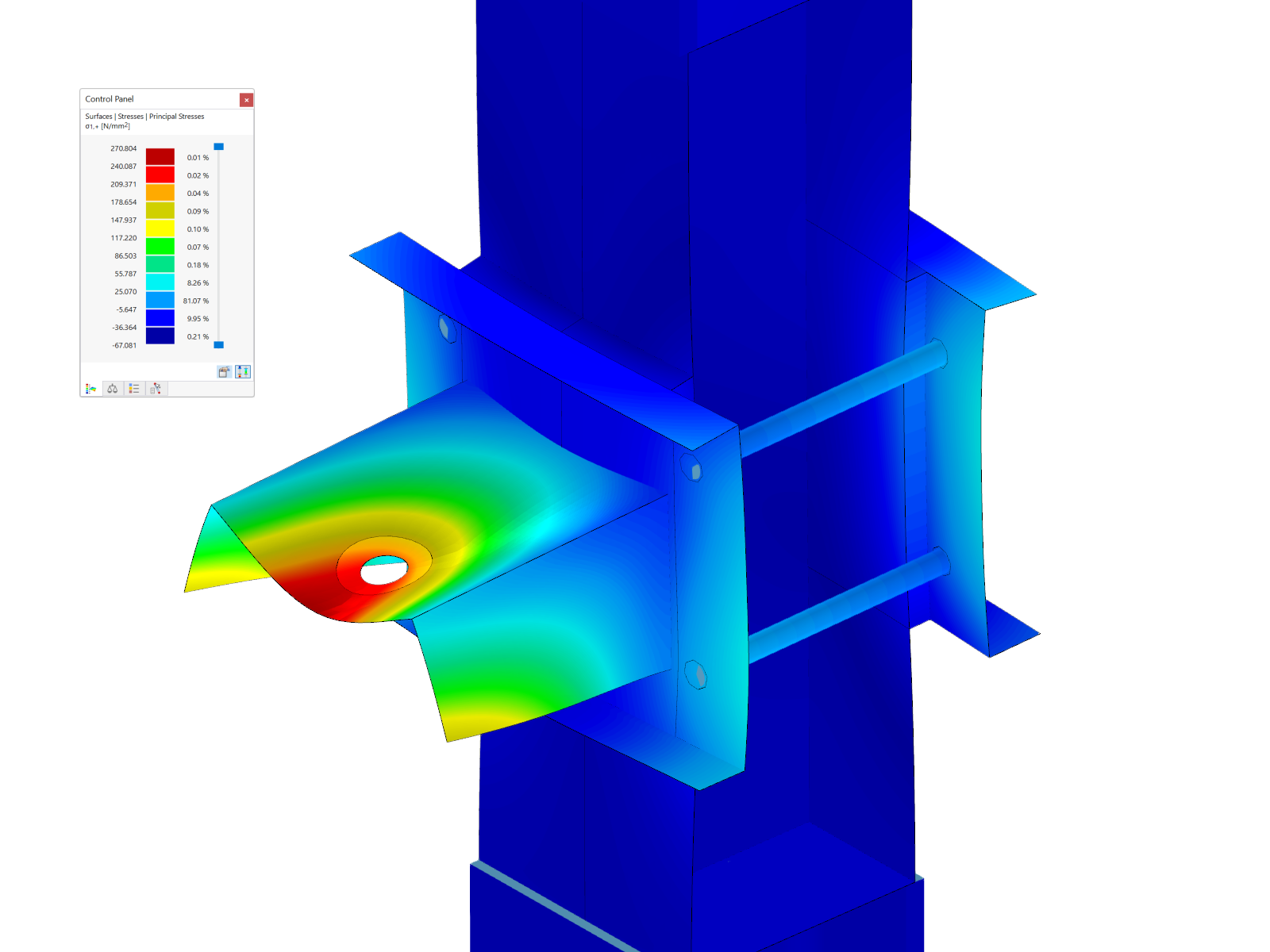
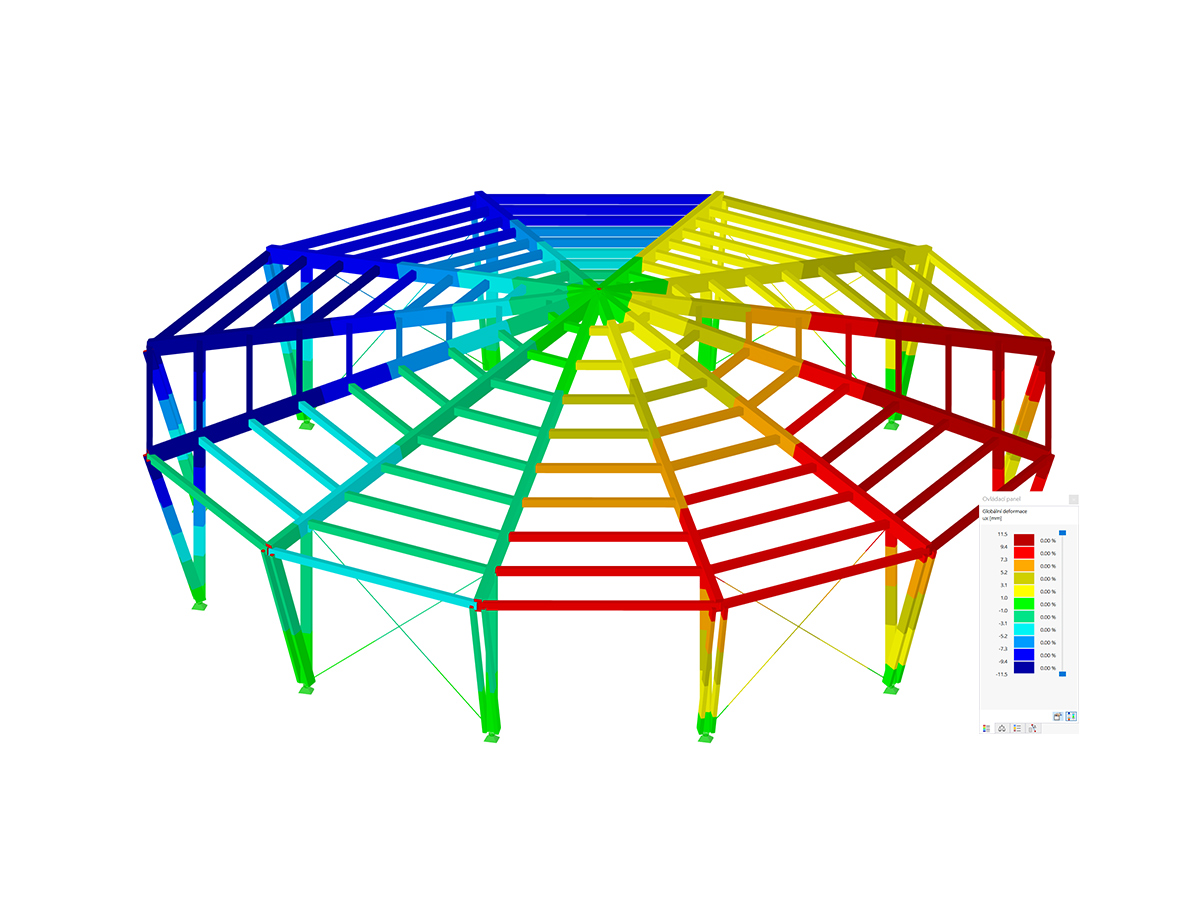
In the case of the yield stress rule according to von Mises, the yield criterion as a circular cylinder with hydrostatic axis is in the principal stress space. All stress states within this space are entirely elastic. Stress states outside this space are not allowed.
Alternatively, you can define the yield rule according to Tresca; in this case, the plastic yielding occurs as a result of the maximum shear stress.
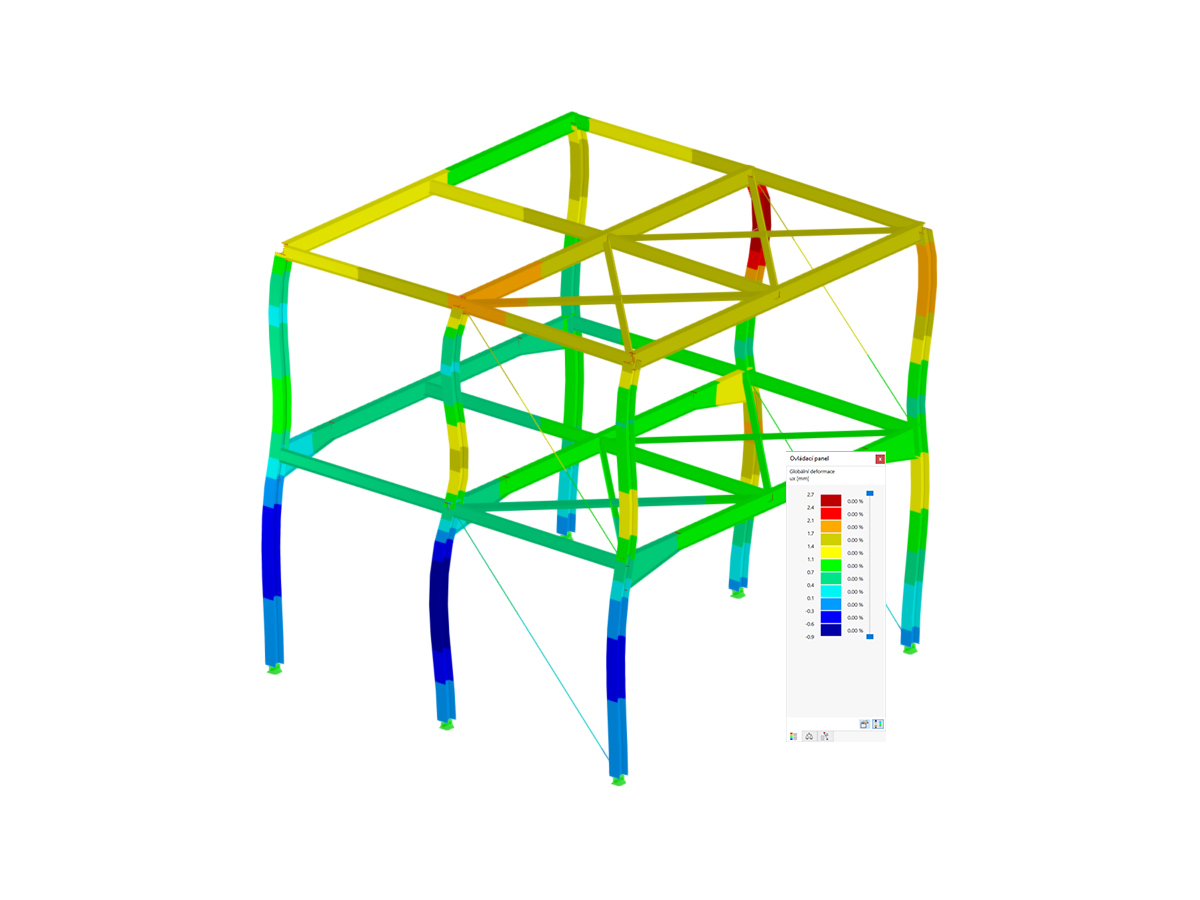
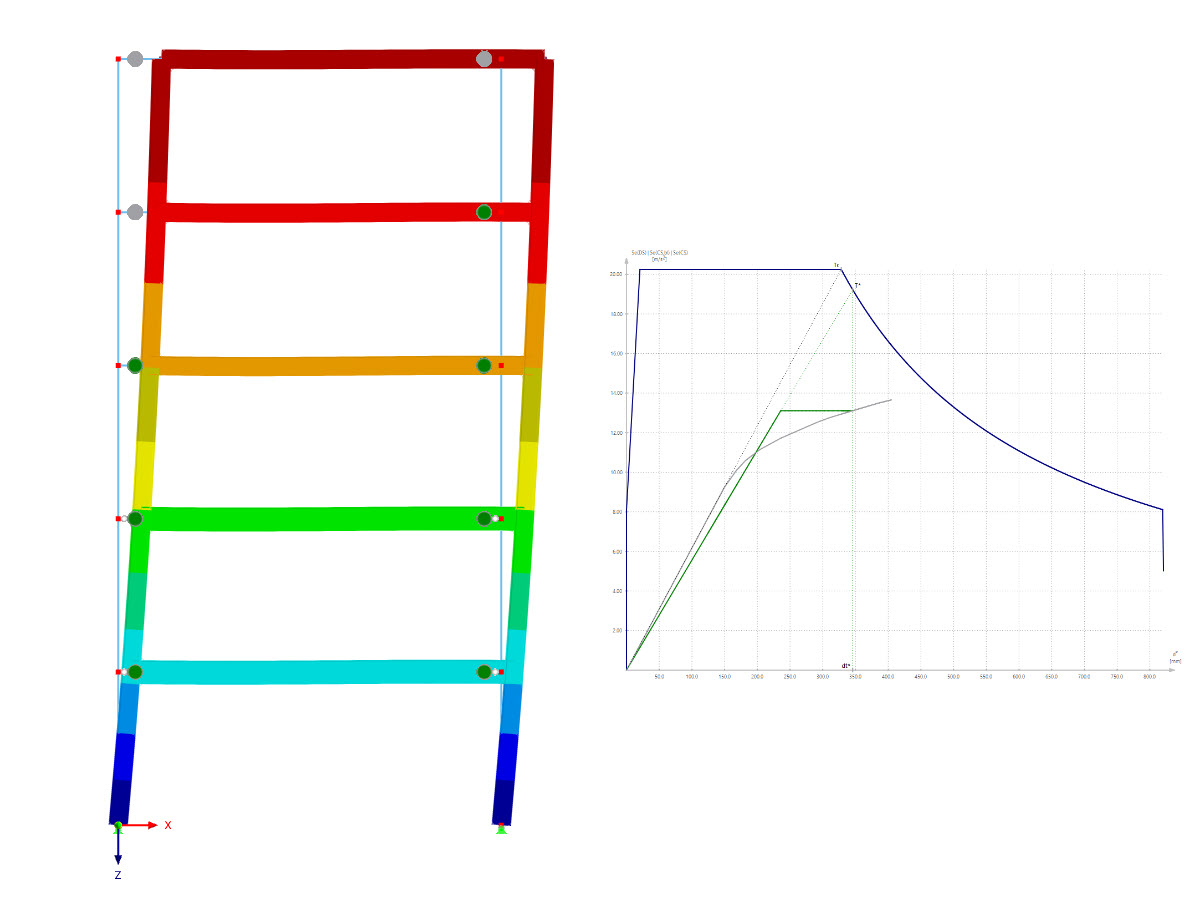
Both yield rules require that - due to the shape of the circular cylinder - the stress-strain relations must be symmetrical in the negative and in the positive zones. Using a time discretization, the yield criteria are numerically integrated by the implicit Euler method. In RFEM, the discretization is implemented in the individual load steps.
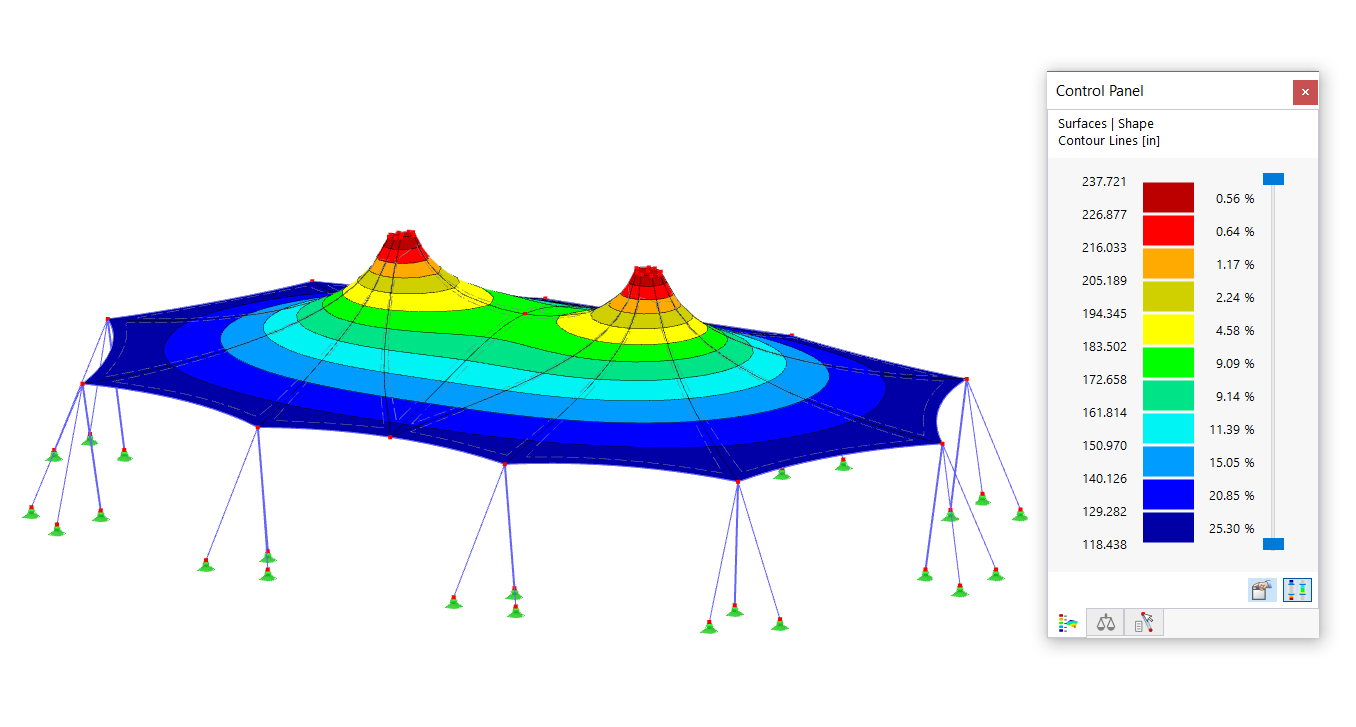
As an extension of the yield criteria, there are the yield rules according to Drucker-Prager and Mohr-Coulomb. In this case, plastic yielding occurs when the maximum shear stress is locally exceeded. In the case of the rule according to Drucker-Prager, there is a continuous surface area in the principal stress space. In the case of the yield rule according to Mohr-Coulomb, there is a discontinuous surface area with a hexagonal cone.
Due to this yield surface, you can define the stress-strain relation of the diagram in the negative zone as asymmetrical. However, the relation must always be within the surface area of the yield rule. The image above shows the surface area for the yield rule according to Drucker-Prager.
















.png?mw=350&hash=c6c25b135ffd26af9cd48d77813d2ba5853f936c)
















.png?mw=512&hash=4a84cbc5b1eacf1afb4217e8e43c5cb50ed8d827)
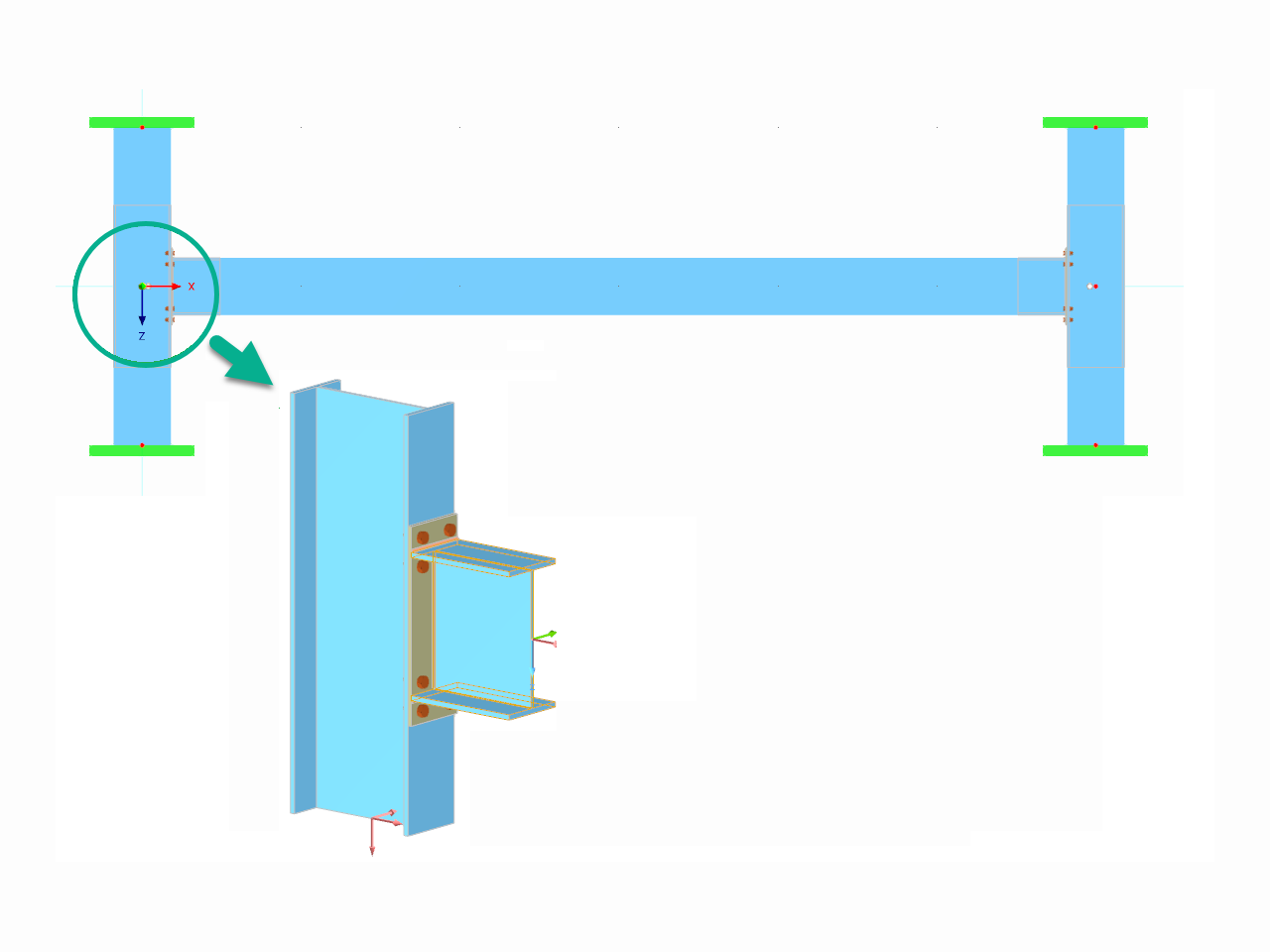








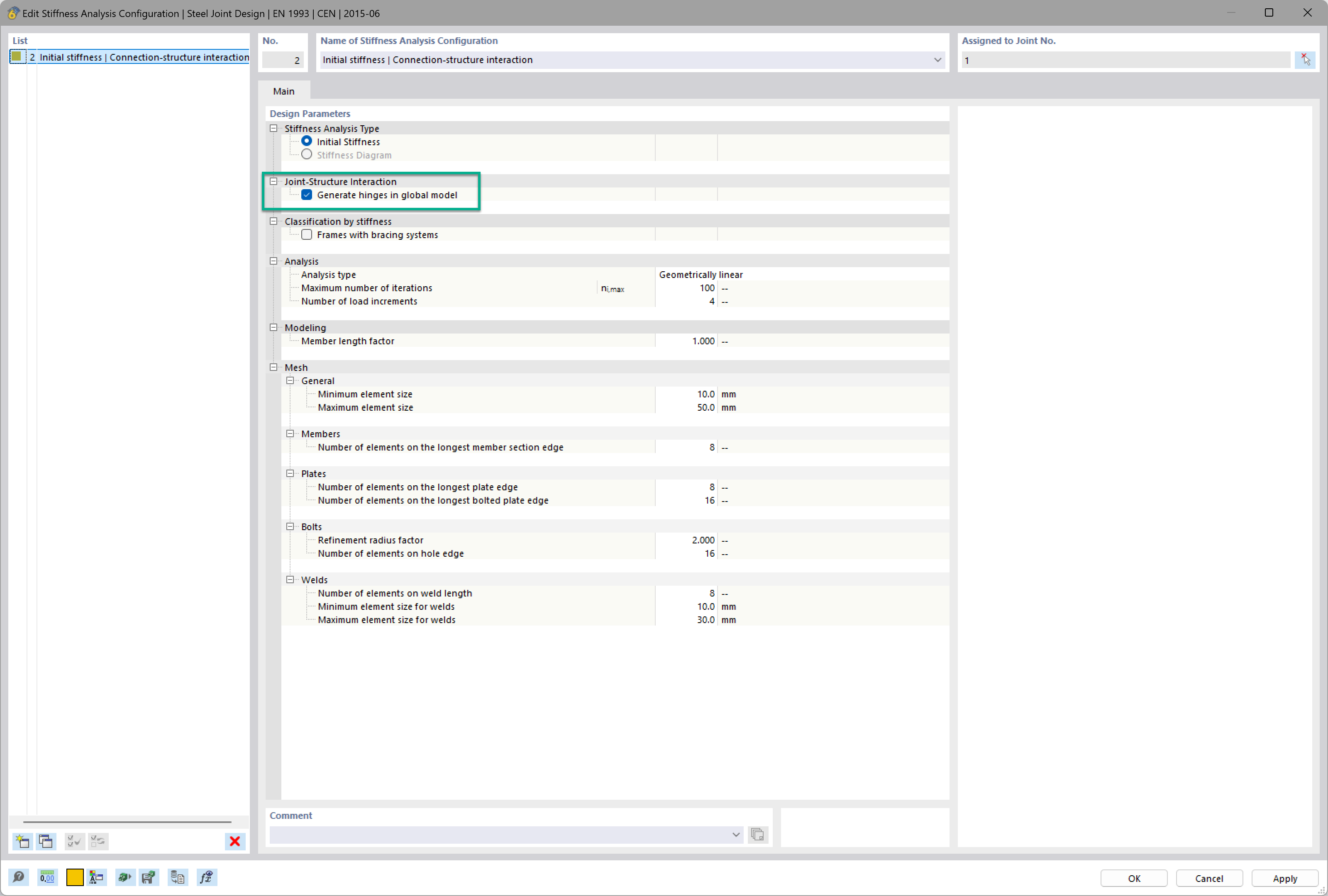

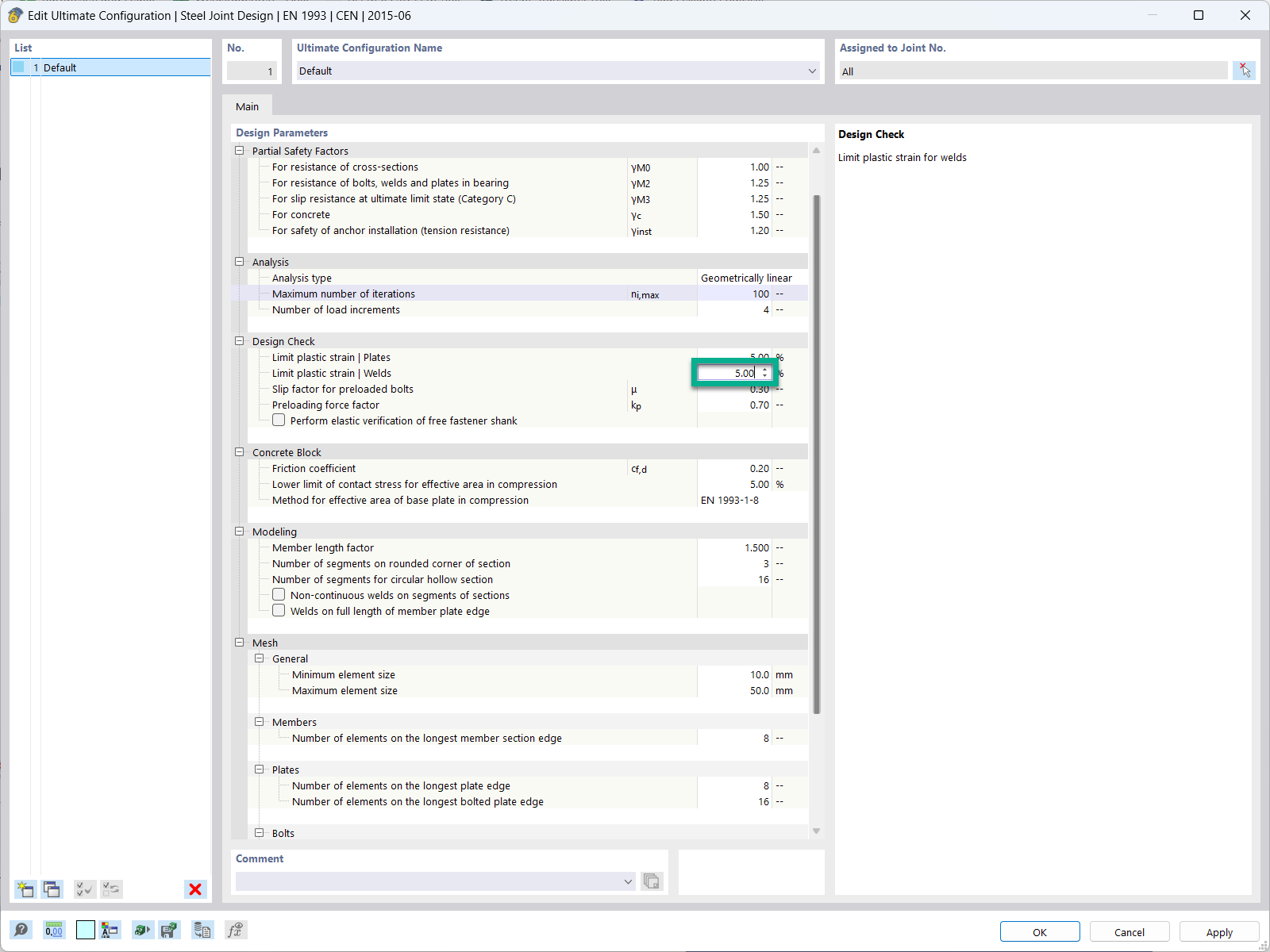




_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)




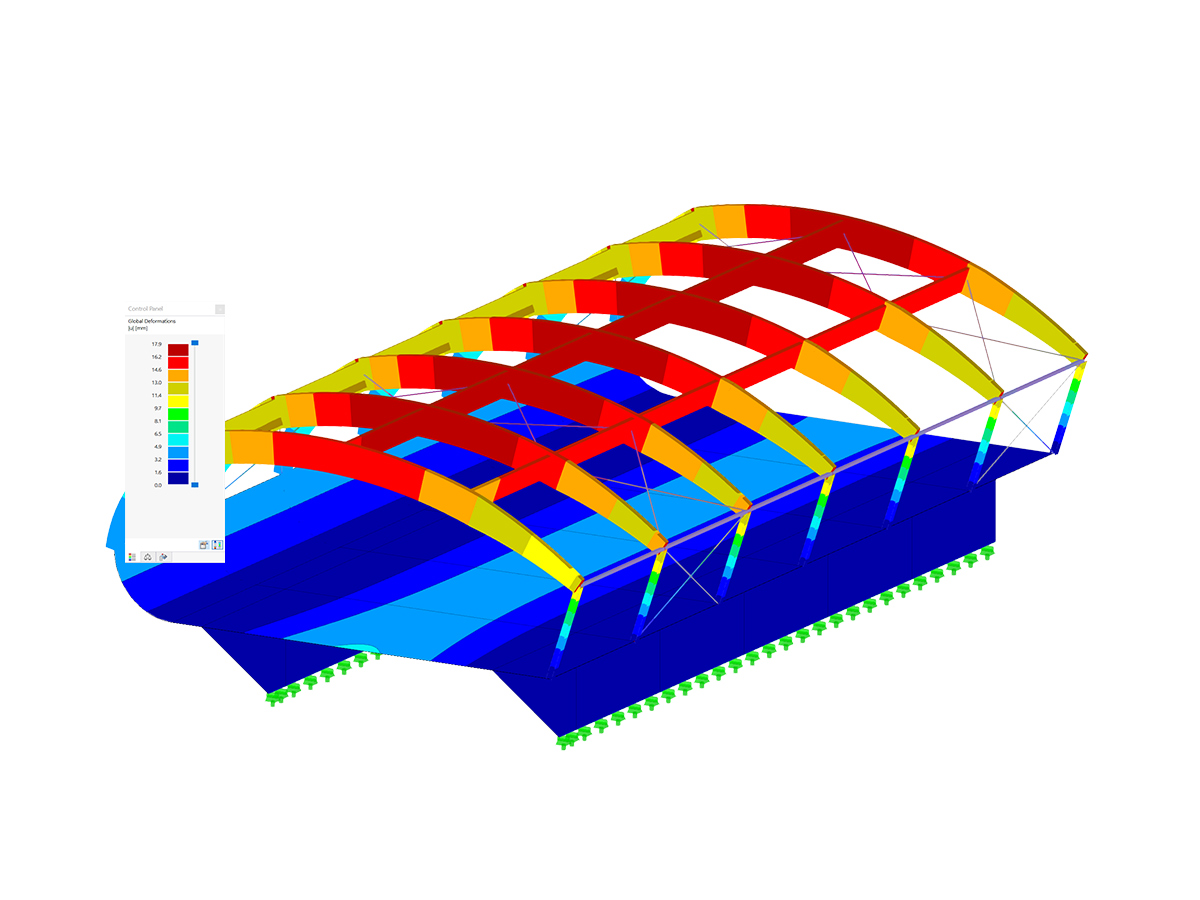
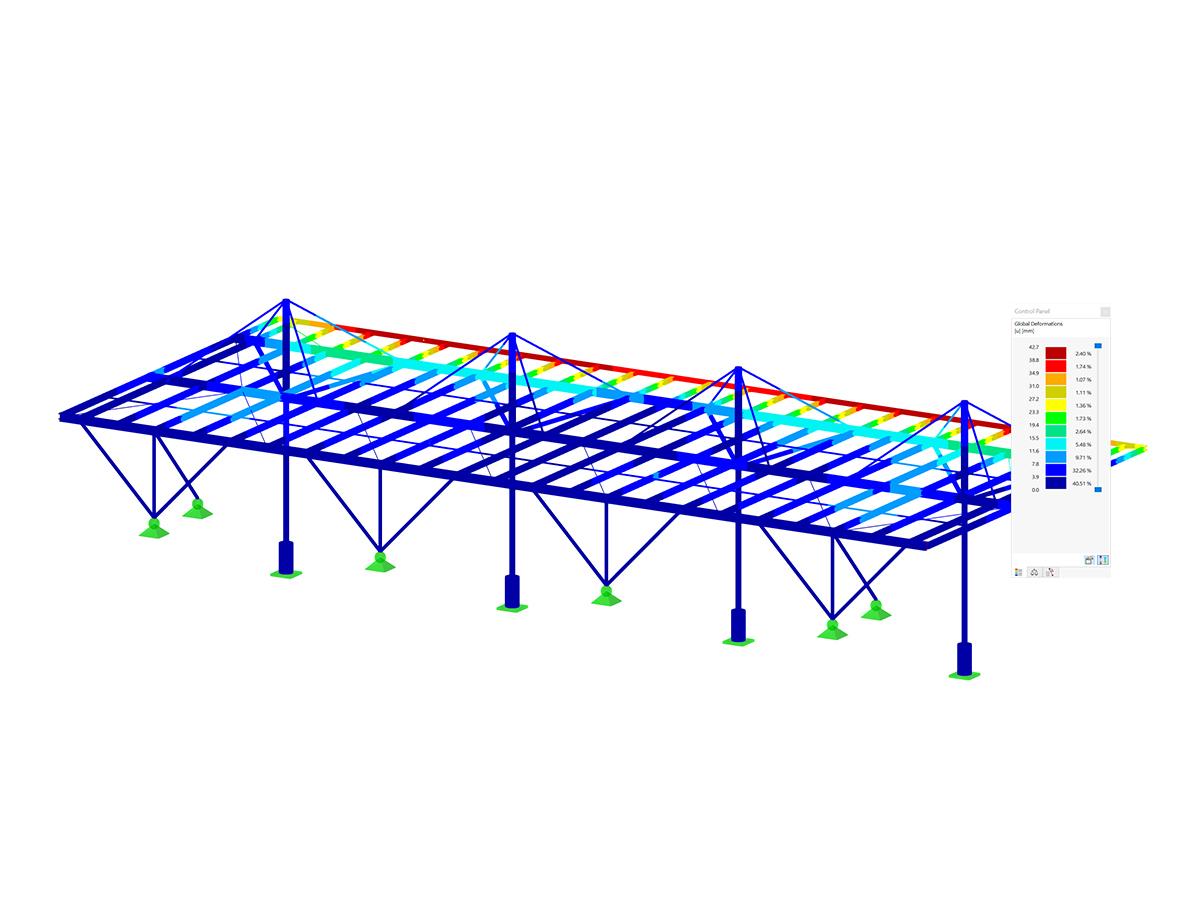
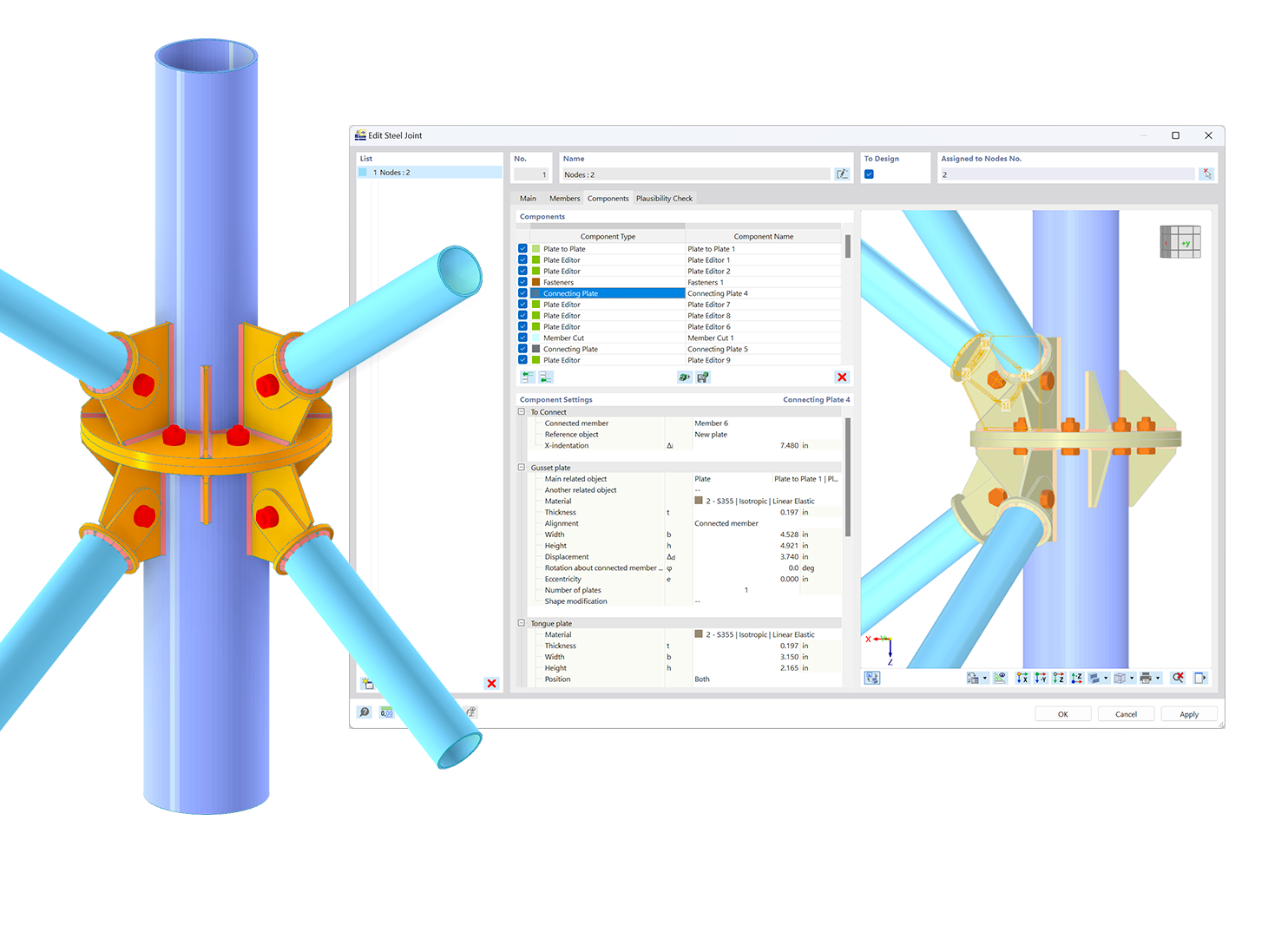.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)