Materials are required to define surfaces, cross-sections, and solids. The material properties affect the stiffnesses of these objects.
Name
You can define any name for the material. If the description matches an entry in the library, RFEM imports the stored material properties. To select a material from the library, click the
![]() button at the end of the input line. The import of materials is described in the chapter Material Library.
button at the end of the input line. The import of materials is described in the chapter Material Library.
For materials from the library, the "Basic Material Properties" are set by default and cannot be changed. If you want to use user-defined properties of the material, select the User-defined material check box in the "Options" section (see the section User-Defined Material).
Main
The Main tab manages the basic material parameters.
Material Type
The material type is used to define the category of the material. It controls the parameters and factors relevant for the design. The material type also defines the partial safety factors of the material, which are taken into account for the design, depending on the standard.
For a material taken from the library, one of the following material types is preset.
Material Model
The following material models are available for selection in the list:
Isotropic Linear Elastic
The linear-elastic stiffness properties of the material do not depend on directions. They can be described as follows:
|
E |
Modulus of elasticity |
|
G |
Shear modulus |
|
ν |
Poisson's ratio |
The following conditions apply:
- E > 0
- G > 0
- −1 < ν ≤ 0.5 (for surfaces and solids; no upper limit for members)
The elasticity matrix (inverse of stiffness matrix) for surfaces is the following:
Orthotropic Linear Elastic (Surfaces)
For this type of material model you can define stiffness properties that appear differently in both surface directions x and y. This allows you to represent the properties of, for example, glass-fiber reinforced plastic, ribbed floors, or the stress directions of reinforced ceilings. The surface axes x and y are perpendicular to each other in the surface plane.
To define different material properties for the x- and y-directions, activate the User-defined material check box in the "Options" section. Then, in the "Orthotropic – Linear Elastic (Surfaces)" tab, you can define the parameters of the material.
The following conditions must be met for a positively definite stiffness matrix:
- Ex > 0; Ey > 0
- Gyz > 0; Gxz > 0; Gxy > 0
Orthotropic Linear Elastic (Solids)
In a three-dimensional orthotropic material model, you can define elastic stiffnesses separately in all directions of the solid. To define different material properties for each direction, activate the User-defined material check box in the "Options" section. Then, in the "Orthotropic – Linear Elastic (Solids)" tab, you can define the parameters of the material.
The stiffness matrix elements determined from the entered data are specified in the "Orthotropic – Linear Elastic (Solids) – Stiffness Matrix" tab.
Isotropic Timber Linear Elastic (Members)
This material model can be selected for materials of the "Timber" type. It allows you to represent, for example, the properties of an oriented strand board (OSB) in a member model, including different stiffnesses depending on the installation position. You can define the position of the board in the "Isotropic Timber | Linear Elastic (Members)" tab using the two lists.
Orthotropic Timber Linear Elastic (Surfaces)
This material model can be used for "Timber" type materials to control the modulus of elasticity with regard to the load-bearing capacity as a wall or panel as well as the shear modulus Gxy: For example, oriented strand boards have directional stiffnesses depending on the position of installation in the model.
The stiffness parameters can be defined in the "Orthotropic Timber | Linear Elastic (Surfaces)" tab. Default values are preset for timber materials from the library. To define different material properties for each direction, first activate the User-defined material check box in the "Options" section (see the section User-Defined Material).
Modulus of Elasticity
The modulus of elasticity E describes the ratio between normal stress and strain.
Shear Modulus
The shear modulus G, also known as the sliding modulus, is the second parameter for describing the elastic behavior of a linear, isotropic, and homogenous material. In this case, the deformation is based on shear stress.
Poisson's Ratio
Poisson's ratio ν is required to determine the transverse strain. Generally, Poisson's ratio for isotropic materials is between 0.0 and 0.5. Therefore, for a value of 0.5 or higher (for example, rubber), it is assumed that the material is not isotropic.
The relation between the modulus of elasticity, shear modulus, and Poisson's ratio for an isotropic material is described in the equation Poisson's Ratio.
When entering a user-defined material with its isotropic properties, RFEM determines the Poisson's ratio based on the values of the modulus of elasticity and the shear modulus. If necessary, you can change this presetting in the "Definition type" list.
Definition Type for Material Properties
| E | G | (ν) | The Poisson's ratio is determined from the modulus of elasticity and the shear modulus. |
| E | (G) | ν | The shear modulus is determined from the modulus of elasticity and the Poisson's ratio. |
| E | G | ν | The modulus of elasticity, shear modulus, and Poisson's ratio are independent of each other. |
Specific Weight / Mass Density
The specific weight γ describes the weight of the material per volume unit. The specification is especially important for the "Self-weight" load type. The automatic self-weight of the model is determined from the specific weight and the cross-sectional areas of the used members or surfaces and solids.
The density ρ describes the mass of the material per volume unit. This information is required for dynamic analyses.
Coefficient of Thermal Expansion
The coefficient of thermal expansion α describes the linear correlation between changes in temperature and length (elongation of material due to heating, shortening due to cooling).
The coefficient of thermal expansion is relevant for the "Temperature" and "Temperature change" load types.
User-Defined Material
The material properties for materials from the library are preset. Therefore, they cannot be changed directly in the text boxes.
To adjust the properties of a material, select the User-defined material check box in the "Options" dialog section. Then, the text boxes in the "Basic Material Properties" dialog section of the "Main" tab become accessible. Use the "Material Values" tab to also change design-specific properties.
If there is a material with orthotropic properties, you can use the "Orthotropic" tab to adjust the modulus of elasticity and the shear modulus as well as the Poisson's ratios (see the image Stiffness Matrix for Orthotropic Linear Elastic Material). If you activate the "Set stiffness matrix elements" option, you can also define the stiffness matrix elements manually.
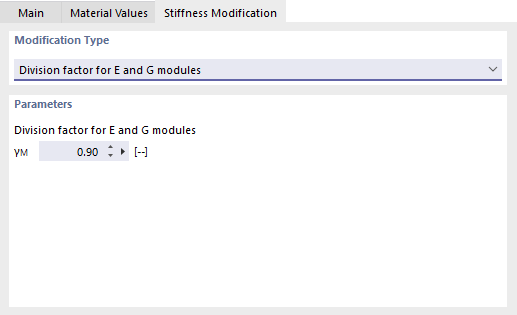
Stiffness Modification
In the case of a user-defined material, you can adjust the stiffness, for example, to consider safety factors or reduced material properties. Two options are available for selection in the "Modification Type" list:
- Division factor for E and G moduli
- Multiplier factor for E and G moduli
In the "Parameters" section, enter the factor by which the material stiffness is to be adjusted.
Temperature-Dependent
To define a linear elastic material with temperature-dependent stress-strain properties, select the User-defined and Temperature-dependent check boxes in the "Options" section. Then, you can define the temperature-dependent material properties in the "Temperature-Dependent" tab. These material properties are taken into account for objects that are thermally stressed by temperature or temperature change. When calculating the temperature loads, the final temperature of the respective step is used.
In the "Temperature-Dependent Property" list, select a material property; for example, the modulus of elasticity. Then, use the
![]() button to create the required table rows so that you can enter the temperatures with the corresponding values row by row. You can use the
button to create the required table rows so that you can enter the temperatures with the corresponding values row by row. You can use the
![]() button to import data from an Excel spreadsheet.
button to import data from an Excel spreadsheet.
The "Reference Temperature" defines the stiffnesses for the objects that have no temperature loads. When a reference value, for example, of 300 °C is set, the reduced modulus of elasticity of that point of the temperature curve is applied for all members and surfaces.