Параметры статического расчета ( SA ) задают правила, по которым рассчитываются загружения и сочетания нагрузок. Предустановлены три стандартных типа анализа.
Основное
Вкладка Основные управляет настройками расчета конструкций и параметрами элементарного расчета.
Тип расчёта
Этот раздел диалога управляет теорией расчета, в соответствии с которой анализируются загружения и сочетания нагрузок. В списке 'Тип анализа' доступны для выбора три подхода.
Геометрически линейный
При расчете по геометрически линейному расчету (первый порядок) равновесие анализируется на недеформированной конструктивной системе. Линейный расчет выполняется, поскольку деформации компонентов не учитываются.
Загружения по умолчанию рассчитываются согласно геометрически линейному расчету.
Нелинейный (P-Δ)
В «конструктивном» анализе второго порядка равновесие определяется на деформированной конструктивной системе. Деформации предполагаются небольшими. Осевые силы в системе влияют на увеличение изгибающих моментов. Таким образом, этот расчет вступает в силу, когда осевые силы значительно превышают силы сдвига.
Сочетания нагрузок по умолчанию рассчитываются нелинейно в соответствии с анализом второго порядка.
Большие деформации
При расчете больших деформаций (третий порядок или теория больших деформаций) учитываются продольные и поперечные силы. После каждого шага итерации создается матрица жесткости деформируемой системы. Нагрузки обрабатываются дифференцированно: Нагрузка, заданная в общем направлении, сохраняет свое направление при кручении конечных элементов. Если нагрузка действует в направлении оси местного стержня или поверхности, она меняет свое направление в соответствии с кручением элемента '.
Если модель включает в себя вантовые стержни, предварительно задан расчет по расчету больших деформаций.
Итерационный метод для нелинейного расчета
В зависимости от типа анализа, существуют различные методы решения нелинейной алгебраической системы уравнений.
Ньютона-Рафсона
Решение в соответствии по Ньютону-Рафсону предуставновлен для большого анализа деформаций. Нелинейная система уравнений решается численно с помощью итерационных приближений с касательными. Матрица тангенциальной жесткости определяется как функция текущего состояния деформации; он инвертируется в каждом цикле итераций. В большинстве случаев, достигается быстрая (квадратичная) конвергенция.
Расчет по Ньютону-Рафсону и по Пикару
Сначала применяется подход по picard Picard . После нескольких итераций выполняется переключение на метод newton-raphson Newton-Raphson . Основная идея этого подхода состоит в том, чтобы использовать относительно «нечувствительный» метод Пикара для первых шагов итерации, чтобы избежать сообщений о нестабильности. За данным начальным приближением следует быстрый метод согласно Ньютона-Рафсона для нахождения пределного состояния равновесия.
по Пикару
Метод по Пикару, также известный как метод секущих, можно понимать как разностную аппроксимацию метода newton-raphson Ньютона-Рафсона . Учитывается разница между текущей и исходной итерацией на шаге приращения текущей нагрузки. Часто сходимость происходит медленнее, чем в методе расчета по Ньютону-Рафсону. Однако он также оказывается менее чувствительным к нелинейным задачам, что делает расчет более устойчивым.
Ньютона-Рафсона с посткритическим расчётом
Этот метод полезен для решения посткритических проблем, требующих преодоления ряда нестабильностей. Если имеется неустойчивость и матрица жесткости не может быть инвертирована, используется матрица жесткости последнего стабильного шага итерации. Расчет с помощью матрицы продолжается до тех пор, пока снова не будет достигнут диапазон устойчивости.
Динамическая релаксация
Последний метод подходит для расчетов по методу больших деформаций и для решения посткритических проблем. В этом подходе вводится искусственный параметр времени. С учетом инерции и затухания, ошибка может быть обработана как динамическая проблема. В этом подходе используется явный метод интегрирования по времени; матрица жесткости не инвертируется. Никакой части модели не разрешается иметь равный нулю удельный при расчете с динамической релаксацией.
Этот метод также включает в себя затухание Рэлея, которое может быть определено с помощью констант α и β в соответствии со следующим уравнением с производными по времени:
| M | Матрица сосредоточенных (диагональных) масс |
| C | Диагональная матрица затухания C = α M + βdiag [K11 ( u ), K22 ( u ), ..., Knn ( u )] |
| K | Матрица жесткости |
| f | Вектор внешних сил |
| U | Дискретный вектор перемещения |
Проверки для нелинейного расчета
' Максимальное количество итераций ' определяет, сколько прогонов вычислений выполняется не более чем для анализа по второму порядку. или расчет больших деформаций, а также для нелинейно действующих объектов. Когда расчет достигает предела без достижения равновесия, появляется соответствующее сообщение. Затем вы можете решить, хотите ли вы отобразить результаты.
' Количество приращений нагрузки ' актуально для расчетов по второму порядку или расчёт по большим деформациям. Часто бывает трудно найти равновесие при учете больших деформаций. Нестабильности можно избежать, применив нагрузку в несколько этапов. Например, если вы укажете два приращения нагрузки, на первом шаге будет приложена половина нагрузки. Потом будут осуществляться итерации до тех пор, пока не будет найдено равновесие. Затем, на втором этапе, к уже деформированной системе прилагается полная нагрузка, и итерации повторяются до тех пор, пока не будет достигнуто равновесие.
Опции I
В этом разделе диалога вы можете активировать различные 'специальные настройки' для управления вычислениями в соответствии со вторым порядком или расчёт по большим деформациям.
Изменение стандартных настроек точности и допуска
Когда вы устанавливаете флажок ' Изменить настройки стандартной точности и допуска ', в диалоговое окно добавляется вкладка precisionAndToleranceTab . Здесь вы можете настроить критерии сходимости.
Игнорировать все нелинейности
С помощью флажка 'Игнорировать все нелинейности' можно отключить нелинейные свойства элементов для расчета. Таким образом, например, растянутые стержни остаются в модели, как только возникают сжимающие силы. Однако вы должны подавлять нелинейные свойства только в тестовых целях; например, чтобы найти причину нестабильности. Неправильно определенные критерии отказов иногда приводят к обрывам в расчетах.
Опции II
Изменить нагрузку множителем
После установки флажка вы можете определить коэффициент k, на который должны быть умножены все нагрузки.
В расчете на устойчивость для увеличения эффектов согласно расчету по методу второго порядка, старые стандарты предполагают умножение нагрузки в целом на определенный коэффициент. С другой стороны, расчет должен быть выполнен с характерными нагрузками. Оба требования могут быть выполнены, если ввести коэффициент больше 1 и установить флажок ' Разделить результаты по коэффициенту нагрузки '.
Для расчетов в соответствии с действующими стандартами нагрузку не следует редактировать с помощью коэффициентов. Вместо этого в расчетных ситуациях следует учитывать частичные коэффициенты надежности и сочетания для наложения.
Учет благоприятного эффеккта от растяжения в стержнях
Растягивающие усилия благоприятно влияют на предварительно деформированные констурктивные системы. Таким образом, деформация снижается, а конструкция стабилизируется. Обычно этот эффект используется в расчетах по методу второго порядка и расчету больших деформаций; например, для залов с подкосами или общих конструкций, подверженных изгибу. Разгрузка от эффектов силы растяжения для балок, скрепленных снизу (балки с опорными стяжками или тросами), может привести к нежелательному уменьшению деформаций и внутренних сил.
Проверка устойчивости по скорости деформации
Если вы установите флажок, RFEM проверяет, как деформации развиваются в ходе итераций во время расчета. Если смещения или повороты резко увеличиваются и превышают внутренний предел программы, расчет прерывается с сообщением о нестабильности.
Попробовать расчитать неустойчивую конструкцию
С помощью этого флажка вы можете попытаться сделать нестабильную модель рассчитываемой: На первом этапе расчета программа RFEM применяет небольшие пружины, стабилизирующие модель для первой итерации. По достижении стабильного начального состояния пружины снимают для последующих итераций.
Перемещения от нагрузки на стержень типа ' Внутреннее давление трубы '
Флажок актуален для нагрузки на стержень, называемой внутренним давлением трубы. Эффект Бурдона описывает усилие изогнутой трубы выпрямиться под действием давления. Как напряжения по периметру, так и осевые напряжения, вызванные нагрузкой от внутреннего давления, приводят к продольной деформации трубы с учетом жесткости материала и поперечной деформации.
См. Техническую статью, в которой описан пример расчета внутреннего давления в трубопроводах.
Сохранить результаты всех приращений нагрузок
Если нагрузка применяется постепенно (см. Loadteps Controls for Nonlinear Analysis ), вы можете использовать этот флажок для принудительного вывода промежуточных результатов, чтобы проверить результаты отдельных приращений нагрузки.
Несимметричный прямой решатель
Решатель несимметричного прямого уравнения используется для нелинейной модели материала (см. Главу Нелинейное поведение материала ) с асимметричными свойствами для растяжения и сжатия. Флажок позволяет вам использовать это средство решения уравнений также для других моделей материала, таких как модель изотропного нелинейного упругого материала.
Равновесие для недеформированной конструкции
Флажок позволяет анализировать недеформирующуюся конструкцию, то есть конструктивную систему, деформации которой остаются нулевыми. Этот вариант расчета может быть полезен, когда система находится под напряжением, например, из-за загружения, в то время как результирующие деформации можно рассматривать как исчезающие.
Одна из областей применения для расчета равновесия недеформированной конструкции - это первичное напряженное состояние геотехнического расчета. В рамках загружения или сочетания нагрузок необходимо определить действующие напряжения, возникающие в результате предварительного нагружения грунта. Однако деформации такого загружения или сочетания не представляют интереса и, следовательно, не являются предметом дальнейшего использования.
Основные параметры
Вкладка Основные параметры управляет основными характеристиками для расчета.
Соотношение постоянной нагрузки
Флажок 'Определить для сочетаний нагрузок' предлагает возможность определить соотношение постоянно действующей нагрузки в сочетании нагрузок. Выберите сочетание нагрузок в списке или создайте новое сочетание нагрузок с помощью кнопки
![]() . Затем в списке 'Сравнить результирующее значение' вы можете определить соотношения, которые имеют статический или переменный эффект.
. Затем в списке 'Сравнить результирующее значение' вы можете определить соотношения, которые имеют статический или переменный эффект.
Соотношение постоянной нагрузки можно рассматривать как соответствующее нормативам при расчете.
Метод для системы уравнений
Обе опции управляют методами, используемыми для решения системы уравнений. Для предотвращения недоразумений: Даже когда система уравнений решается напрямую, итерационный расчет выполняется при наличии нелинейностей или если расчеты выполняются по методу второго порядка. или расчёт по большим деформациям. ' Прямое 'и' Итеративное ' относятся к управлению данными во время расчета.
Какой метод решателя матриц быстрее приводит к результатам, зависит от сложности модели, а также от размера доступной основной памяти (ОЗУ). Для малых и средних систем более эффективен прямой метод.
Для очень больших и сложных систем итерационный метод приводит к более быстрым результатам.
Теория изгиба пластин
Поверхности можно рассчитать по теориям изгиба 'Миндлина' или ' Кирхгофа '. В расчете по Миндлину учитываются деформации сдвиговой силы; по словам Кирхгофа, они не учитываются. Таким образом, вариант расчета Mindlin подходит для относительно толстых пластин и оболочек, используемых в прочном строительстве, а вариант Кирхгофа рекомендуется для относительно тонких поверхностей, таких как металлические листы в стальных конструкциях.
Параметры итерационного метода
Флажки в этом разделе диалога важны для анализа ' второго порядка (P-Δ) '.
Отнести внутренние силы к деформированной конструкции
Внутренние силы и моменты стержней обычно отображаются по отношению к измененному положению систем координат стержня, возникающих в деформированной системе. Если вы хотите, чтобы выходные данные относились к недеформированной исходной системе, вы можете определить соответствующие внутренние силы и моменты на стержне, сняв соответствующие флажки.
Процент итераций метода Ньютона-Рафсона в сочетании с методом Пикара
Метод по Пикару основан на секущих жесткостях, а метод Ньютона-Рафсона - на касательных. Когда выбран вариант расчета Ньютон-Пикард Ньютон-Рафсон в сочетании с опцией расчета Пикара , на первых итерациях используются секущие жесткости, а затем для остальных итераций применяются касательные жесткости. Отношение первых итераций с секущими жесткости связано с общим количеством итераций.
Пребразование массы в нагрузку
Нагрузки можно определять не только как силы и моменты, но и в виде масс. Однако массы не влияют на расчет конструкций. Если вы хотите их учитывать, установите флажок ' Активная масса '. Затем введите коэффициент ' в направлении ', чтобы описать влияние массы. Таким образом, массы преобразуются в силы до начала расчета, и они включаются в определение внутренних сил и моментов.
Используйте кнопку
![]() для переключения между вводом коэффициента массы и непосредственным вводом ускорения. Соответственно изменяются названия полей ввода.
для переключения между вводом коэффициента массы и непосредственным вводом ускорения. Соответственно изменяются названия полей ввода.
Возобновление
Вкладка Реактивация становится доступной, как только в модели существует стержень с нелинейными свойствами. На этой вкладке вы можете управлять тем, как будут обрабатываться в расчете вышедшие из строя стержни.
Выходящие из строя стержни часто являются причиной проблем, связанных с неустойчивостью, например, когда модель стержня усиливается за счет растянутых стержней. Из-за сжатия колонны рамы из-за вертикальной нагрузки на растянутые элементы на первом этапе расчета действуют небольшие сжимающие силы. Они будут удалены из системы. На втором этапе модель становится неустойчивой без этих растянутых стержней. С помощью параметров в разделе диалога 'Повторная активация неисправных элементов' можно попытаться выполнить расчет без сообщения об ошибке.
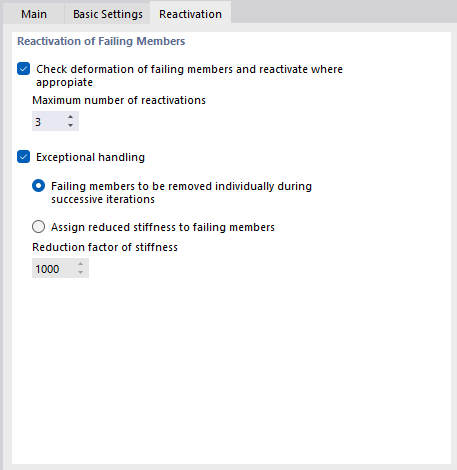
Проверить деформации стержней, вышедших из строя и при необходимости включить их в работу
RFEM анализирует узловые перемещения на каждой итерации. Например, если концы стержней вышедшего из строя растянутого стержня отодвигаются друг от друга, стержень снова используется в матрице жесткости.
В некоторых случаях повторная активация стержней может быть проблематичной: Член удаляется после первой итерации, повторно активируется после второй, снова удаляется после третьей итерации и т.д. Расчет будет запускать этот цикл до тех пор, пока не будет достигнуто максимально возможное количество итераций, без сходимости. ' Максимальное количество повторных активаций ' предотвращает этот эффект. Вы можете определить, как часто элемент стержня может быть повторно вставлен, прежде чем он будет окончательно удален из матрицы жесткости.
Особая настройка параметров
Если вы отметите флажок ' Особая обработка ', вы можете выбрать один из двух методов работы с неисправными стержнями. Их можно комбинировать с реактивацией, описанной выше.
- Вышедшие из работы стержни отстранять индивидуально в последовательных итерациях
После первой итерации программа RFEM удаляет, например, не все растянутые стержни с силой сжатия, а только растянутый стержень с наибольшей сжимающей силой. Затем, во второй данной итерации, в матрице жесткости отсутствует только один стержень. Затем снова удаляют растянутый элемент с наибольшей сжимающей силой. Таким образом, система часто показывает лучшее поведение сходимости из-за эффектов перераспределения.
Этот вариант вычисления длится по времени дольше из-за требуемых в данной программе множественных итераций. Кроме того, необходимо убедиться, что на вкладке 'Основные' указано достаточное loadteps Максимальное количество итераций .
- Стержням, выходящим из строя,
придать редуцированную жесткость
Вышедшие из строя стержни не удаляются из матрицы жесткости, а вместо этого им присваивается очень небольшая жесткость. Вы можете задать его в поле ' Понижающий коэффициент жесткости ': Коэффициент 1000 означает, что жесткость стержня уменьшена до 1/1000.
Точность и допуски
Вкладка « Точность и допуск » позволяет влиять на параметры сходимости и допуска в расчете. Однако изменять настройки по умолчанию следует только в исключительных случаях.
Точность критериев конвергенции в нелинейном расчете МКЭ
Если действуют нелинейные эффекты или если или выполняется расчет на большие деформации, на расчет можно повлиять с помощью критерия сходимости.
Происходит последовательное сравнение по стержням данного изменения осевых сил двух последних итераций. При достижении данного изменения определенной части суммы максимальной осевой силы вычисление останавливается. Однако во время итераций может случиться так, что осевые силы будут колебаться между двумя значениями. Вы можете предотвратить этот эффект маятника, отрегулировав «чувствительность».
Точность также влияет на критерий сходимости изменений деформации в расчетах, выполняемых по методу больших деформаций, где учитываются геометрические нелинейности. Значение по умолчанию - 1,00. Минимальный коэффициент - 0,01, максимальное значение - 100,00. Чем меньше значение, тем ближе должен быть член сходимости к члену сравнения. Соответственно повышается точность результата.
Допуск для определения потери устойчивости
Существуют разные подходы к анализу поведения модели на устойчивость. Однако ни один из них не может с абсолютной надежностью обнаружить сингулярные матрицы жесткости.
RFEM использует две процедуры для определения нестабильности: С одной стороны, элементы на главной диагонали матрицы жесткости всегда сравниваются абсолютно с одинаковыми номерами в итерациях. С другой стороны, каждый элемент главной диагонали анализируется относительно соседнего числа. Допуск можно отрегулировать в полевых условиях. Чем меньше значение допуска, тем ближе предел неустойчивости модели ' смещен к точному местоположению неустойчивости. Соответственно повышается точность результата.
Относительная установка шага времени для динамической релаксации
Параметр времени управляет расчетом по методу динамическая релаксация . Чем меньше значение, тем меньше шаг по времени, с помощью которого регистрируются все колебания реакции. Соответственно повышается точность результатов.
Корректность итерационного расчета
В случае проблем сходимости с методом Ньютона-Рафсона, устойчивость может быть усилена, чтобы предотвратить «пропуск» решения. При уменьшении значения количество возможных решений уменьшается в случае наличия несходящейся горизонтальной ветви решения, и, таким образом, уменьшается также возможность получения действительного результата в пределах заданных итераций. Возможно, потребуется увеличить максимальное количество итераций.