Ортотропия формы

На вкладке « Ортотропия формы » можно описать ортотропные свойства с помощью геометрических параметров. Программа определяет элементы матрицы жесткости на основе этих спецификаций.

Диалоговое окно 'Новая толщина ', вкладка' Ортотропия формы '

Тип ортотропии

Для выбора в списке доступны различные типы (см. Рисунок выше). Задайте геометрическую форму, которая соответствует ортотропным свойствам толщины.

Раздел диалога 'Параметры' адаптирован к типу ортотропии, поэтому вы можете описать геометрию соответствующим образом. Отдельные типы описаны ниже в описании Parameters .

направление ортотропии

Ортотропные свойства относятся к системе осей xy соответствующих поверхностей (см. Графику в диалоговом окне). Если жесткости не соответствуют ориентации системы осей поверхности, вы можете настроить направление в этом разделе диалога.

Отрегулируйте ортотропное направление

Положительный угол β поворачивает ортотропные элементы жесткости по часовой стрелке вокруг положительной оси z поверхности. Матрицы преобразуются соответствующим образом и отображаются на вкладке transformed-matrix Transformed Stiffness Matrix .

Учет собственного веса

При использовании ортотропии формы обычно бывает разная толщина в обоих направлениях. Укажите толщину, которую программа должна применить при определении собственного веса. В списке представлены следующие параметры ' определения собственного веса ':

• Определяется по параметрам: Условная толщина определяется из параметров x- и y-направлений.
• Пользовательская фиктивная толщина: Задайте толщину d_g вручную.
• Пользовательский собственный вес: Введите собственный вес w_g как массу на единицу площади.

параметры

В этом разделе диалога задайте геометрические свойства типа ортотропии.

Полезные толщины

Вы можете задать разные толщины в направлениях ортотропии x и y, чтобы представить неравные соотношения жесткостей (см. Изображение image030874 Новая толщина ).

Соединение

С помощью этого типа ортотропии можно представить соединения между поверхностями или стержнями, которые доступны благодаря элементам связи.

Тип ортотропии ' соединение '

Введите толщину соединительных элементов d_p, а также межосевое расстояние a и ширину соединительных элементов b согласно схеме. Дается реалистичная модель соединения, когда расстояние между соединенными элементами больше их ширины.

ребристая плита

Ортотропные свойства ребристого перекрытия основаны на принципе одноосно напряженной плиты Т-образного профиля.

Ортотропия типа ' ребристая плита '

Задайте толщину плиты d_p, высоту ребра d_r, шаг ребра a и ширину ребра b по схеме. На основе этих параметров программа RFEM определяет жесткость для каждого направления.

двунаправленная ребристая плита

Этот тип потолка характеризуется наличием перемычек, которые ортогонально пересекаются друг с другом в виде единой решетки, таким образом, разделяя пол на ящики.

Ортотропный тип ' кессонного потолка '

Задайте толщину плиты d_p и высоту ребра d_r, а также шаг ребра a и ширину ребра b для двух направлений в соответствии со схемой.

Трапециевидный профлист

Трапециевидный лист можно отобразить не только как стержень, но и как поверхность с ортотропными свойствами.

Тип ортотропии ' профлист '

Введите толщину листового металла t, общую высоту профиля h, расстояние между центрами ребер a, а также ширину борта над b_t и ширину борта b_b в соответствии со схемой.

многопустотная плита

Пустотелые блоки, встроенные в потолок, уменьшают собственный вес, но обеспечивают ортотропные свойства конструкции.

Тип ортотропии ' Многопустотная плита '

Введите толщину плиты d_p, шаг впадин a и диаметр впадин b по схеме.

решетчатый настил

Вы можете отобразить ростверк не только как модель стержня, но и как поверхность с ортотропными свойствами.

Тип ортотропии ' Балочная решетка '

Введите толщину плиты d_p, расстояние от центра до центра ребра a и ширину b ребра для двух осей согласно диаграмме.

Матрица жесткости

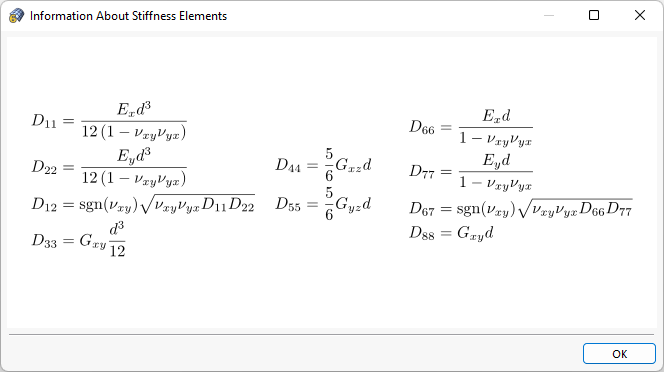
На вкладке «Матрица жесткости » диалогового окна 'Новая толщина' отображаются элементы матрицы жесткости (см. Изображение # extbookmark manual|image020637|Задайте матрицу жесткости №). Записи не могут быть изменены.

Преобразованная матрица жесткости

Если оси ортотропии не согласуются с осями системы координат элементов, необходимо преобразовать матрицы. Соответствующие значения отображаются на вкладке « Трансформированная матрица жесткости ».

Трансформированные элементы матрицы жесткости

Используйте кнопку , чтобы открыть диалоговое окно с информацией для определения элементов матрицы.

Информация об элементах жесткости