2.8.4.1 Berücksichtigung von Kriechen

Berücksichtigung von Kriechen

Das Kriechen beschreibt die zeitabhängige Verformung des Betons unter Belastung über einen bestimmten Zeitraum. Die wesentlichen Einflussgrößen ähneln denen des Schwindens (siehe Kapitel 2.8.4.2). Zusätzlich übt die so genannte „kriecherzeugende Spannung“ einen wichtigen Einfluss auf die Kriechverformungen aus.

Für das Kriechen sind die Dauer der Belastung, der Zeitpunkt der Lastaufbringung sowie die Höhe der Beanspruchung zu beachten. Das Kriechen wird durch die Kriechzahl φ(t,t₀) zum Zeitpunkt t erfasst.

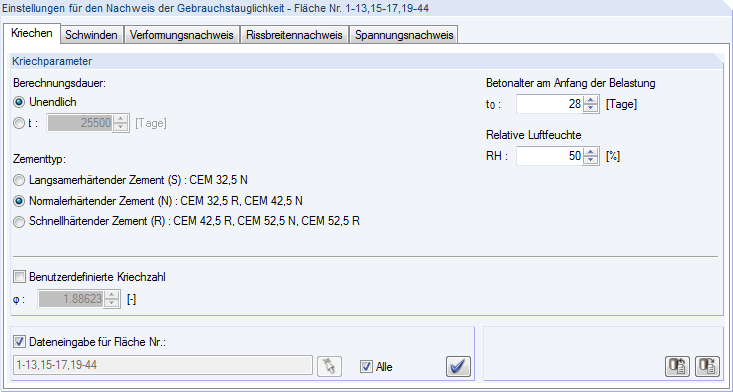
In RF-BETON Flächen erfolgen die Angaben zur Ermittlung des Kriechbeiwerts in der Maske 1.3 Flächen. Dort sind das Betonalter zum betrachteten Zeitpunkt und zu Belastungsbeginn, die relative Luftfeuchte sowie der Zementtyp zu bestimmen. Aus diesen Angaben wird die Kriechzahl φ vom Programm ermittelt.

Die Ermittlung der Kriechzahl φ wird kurz gemäß EN 1992-1-1, Abschnitt 3.1.4 vorgestellt. Voraussetzung für nachfolgend beschriebene Gleichungen ist, dass die kriecherzeugende Spannung σ_c der einwirkenden Dauerlast folgenden Wert nicht überschreitet.

${\sigma }_c \le 0.45 · f_{ckj }$

mit

Tabelle 2.2

fckj	Zylinderdruckfestigkeit des Betons zum Zeitpunkt des Aufbringens der kriecherzeugenden Spannung

Unter Annahme eines linearen Kriechverhaltens (σ_c < 0.45 ⋅ f_ckj) kann das Kriechen des Betons durch eine Abminderung des Beton-Elastizitätsmoduls erfasst werden.

$E_{c,\text{eff}} = \frac{E_{cm}}{1.0 + \phi (t,t_0)}$

mit

Tabelle 2.2

Ecm	mittlerer Elastizitätsmodul nach EN 1992-1-1, Tabelle 3.1
φ (t,t0)	Kriechzahl
t	Betonalter zum untersuchten Zeitpunkt in Tagen
t0	Betonalter zu Belastungsbeginn in Tagen

Gemäß EN 1992-1-1, Abschnitt 3.1.4 darf die Kriechzahl φ(t,t₀) zum untersuchten Zeitpunkt t wie folgt berechnet werden.

$\varphi \left(t,t_0\right) = {\varphi }_{RH} · \beta \left(f_{cm}\right) · \beta \left(t_0\right) · \beta \left(t,t_0\right)$

mit

${\phi }_{RH} = \left[1 + \frac{1 - {\displaystyle \frac{RH}{100}}}{0.10 · \sqrt[3]{h_0}} · {\alpha }_1\right] · {\alpha }_{2 }$

Tabelle 2.2

RH	Relative Luftfeuchte [%]
$h_0 = \frac{2 · A_c}{u}$	Wirksame Bauteildicke [mm] (bei Flächen: h0 = h) Ac  Querschnittsfläche u    Querschnittsumfang
${\alpha }_1 = {\left(\frac{35}{f_{cm}}\right)}^{0.7}$	Anpassungsfaktor fcm  Mittelwert der Zylinderdruckfestigkeit
${\alpha }_2 = {\left(\frac{35}{f_{cm}}\right)}^{0.2}$	Anpassungsfaktor
$\beta \left(f_{cm}\right) = \frac{16.8}{\sqrt{f_{cm}}}$	Beiwert zur Berücksichtigung der Betondruckfestigkeit
$\beta \left(t_0\right) = \frac{1}{0.1 + t_{0.eff}^{0.2}}$	Beiwert zur Berücksichtigung des Betonalters

$t_{0.eff} = t_0 {\left[1 + \frac{9}{2 + t_0^{1.2}}\right]}^{\alpha } \ge 0.5 · d$

Tabelle 2.2

$\beta \left(t,t_0\right) = {\left[\frac{t - t_0}{{\beta }_H + t - t_0}\right]}^{0.3}$	Beiwert zur Berücksichtigung der Belastungsdauer
$t$	Betonalter zum betrachteten Zeitpunkt in Tagen
$t_0$	Betonalter zu Belastungsbeginn in Tagen

${\beta }_H = 1.5 · {\left[1 + {\left(0.012 · RH\right)}^{18}\right]}^{\alpha } · h_0 + 250 · {\alpha }_3 \le 1500 · {\alpha }_{3 }$

Tabelle 2.2

$RH$	Relative Luftfeuchte [%]
$h_0$	Wirksame Bauteildicke [mm]
${\alpha }_3 = {\left(\frac{35}{f_{cm}}\right)}^{0.5}$	Anpassungsfaktor

Der Einfluss des Zementtyps auf die Kriechzahl des Betons kann berücksichtigt werden, indem das Belastungsalter t₀ mithilfe folgender Gleichung verändert wird.

$t_0 = t_{0,T} · {\left(1 + \frac{9}{2 + {\left(t_{0,T}\right)}^{1.2}}\right)}^{\alpha } \ge 0.5$

mit

Tabelle 2.2

t0 = tT	wirksames Betonalter bei Belastungsbeginn unter Berücksichtigung des Einflusses der Temperatur
α	Exponent in Abhängigkeit vom Zementtyp:
	-1 : langsam erhärtende Zemente (S) (32,5) 0 : normal oder schnell erhärtende Zemente (N) (32,5 R; 42,5) 1 : schnell erhärtende hochfeste Zemente (R) (42,5 R; 52,5)

Sind die Dehnungen zum Zeitpunkt t = 0 sowie zu einem späteren Zeitpunkt t bekannt, kann der Kriechbeiwert φ zur rechnerischen Berücksichtigung im Modell bestimmt werden.

${\phi }_t = \frac{{\epsilon }_t}{{\epsilon }_{t=0}} - 1$

Diese Gleichung wird nach der Dehnung zum Zeitpunkt t umgestellt. Es ergibt sich folgender Zusammenhang, der für konstante Spannungen (vgl. Gleichung 2.96) Gültigkeit besitzt:

${\epsilon }_t = {\epsilon }_{t=0} · \left({\phi }_t + 1\right)$

Für größere Spannungen als etwa 0.4 ⋅ f_ck steigen die Dehnungen überproportional an, wodurch der linear angenommene Bezug verloren geht.

Die Berechnung in RF-BETON NL benutzt eine gängige, für baupraktische Zwecke sinnvolle Lösung. Die Spannungs-Dehnungs-Linie des Betons wird um den Faktor (1 + φ) verzerrt.

Wie im Bild 2.146 ersichtlich, handelt es sich bei der Berücksichtigung des Kriechens um den Fall konstanter kriecherzeugender Spannungen über die Belastungszeit. Diese Annahme führt infolge nicht berücksichtigter Spannungsumlagerungen zu einer leichten Überschätzung der Verformung. Der Spannungsabbau ohne eine Dehnungsänderung (Relaxation) wird in diesem Modell nur bedingt erfasst. Geht man von einem linear elastischen Verhalten aus, so könnte eine Proportionalität unterstellt werden und die horizontale Verzerrung würde die Relaxation im Verhältnis (1 + φ) ebenfalls widerspiegeln. Bei der nichtlinearen Spannungs-Dehnungsbeziehung geht dieser Zusammenhang jedoch verloren.

Damit wird deutlich, dass diese Vorgehensweise als Näherung zu verstehen ist. Eine Verminderung der Spannungen infolge Relaxation sowie nichtlineares Kriechen können somit nicht oder nur näherungsweise abgebildet werden.