2.4.1 Bemessungsschnittgrößen

Bemessungsschnittgrößen

Die wesentlichen Formeln zur Bestimmung der Bemessungsnormalkräfte aus den Hauptnormalkräften sind in Gleichung 2.5 bis Gleichung 2.7 im Kapitel 2.3 vorgestellt. Nach Baumann [1] können diese Formeln auch für Momente angewandt werden, da diese nichts anderes sind als ein vom Betrag her gleiches Kräftepaar in einem gewissen Abstand und mit diametraler Richtung.

Platten unterscheiden sich unter anderem dadurch von Wänden, dass die Einwirkungen zu Spannungen unterschiedlichen Vorzeichens auf zwei gegenüberliegenden Plattenseiten führen. Deshalb wäre es sinnvoll, Platten mit Bewehrungsnetzen unterschiedlicher Richtungen für die beiden Plattenseiten auszustatten. Da die Hauptmomente m₁ und m₂ in der Flächen-Schwerebene ermittelt werden, müssen sie auf die Plattenseiten verteilt werden, um die Bemessungsmomente für die Bewehrung der jeweiligen Plattenseite bestimmen zu können.

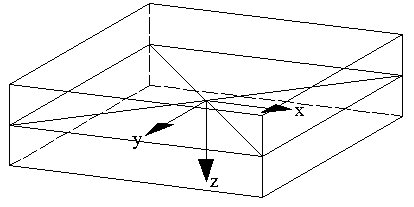
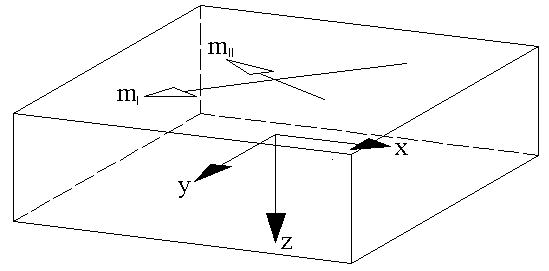
Es wird ein Plattenelement mit seiner Beanspruchung betrachtet. Das lokale Flächen-Koordinatensystem befindet sich in der Schwerebene der Platte.

Die Flächenachsen lassen sich im Zeigen-Navigator über Modell → Flächen → Flächen-Achsensysteme x,y,z oder das Kontextmenü der Flächen einblenden (siehe Bild 3.28).

Die Hauptschnittgrößen m₁ und m₂ werden in RFEM für die Plattenschwerebene ermittelt.

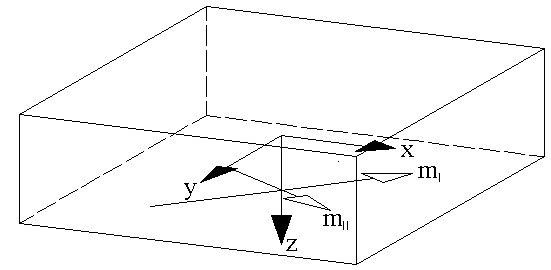
Die Hauptmomente werden als einfache Pfeile dargestellt. Sie sind so orientiert wie die Bewehrung, die zu ihrer Aufnahme nötig wäre.

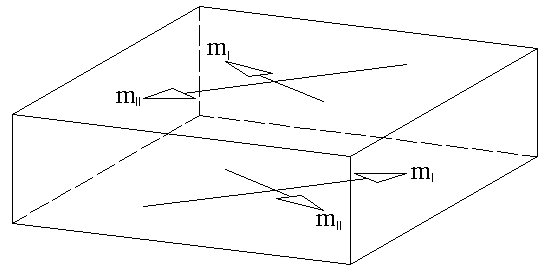
Um aus diesen Hauptmomenten Bemessungsmomente für das Bewehrungsnetz an der Plattenunterseite zu erhalten, werden die Hauptmomente unverändert zur Plattenunterseite verschoben. Diese werden für die Bemessung mit römischen Indizes als m_I und m_II bezeichnet.

Um die Hauptmomente zur Bestimmung der Bemessungsmomente für das Bewehrungsnetz an der Plattenoberseite zu erhalten, werden die Hauptmomente an die Plattenoberseite verschoben. Gleichzeitig wird ihre Richtung um 180° gedreht.

Da üblicherweise das Hauptmoment als m₁ bezeichnet wird, das unter Beachtung des Vorzeichens größer ist (siehe Bild 2.27), müssen die Bezeichnungen der Hauptmomente an der Plattenoberseite noch vertauscht werden.

Die Hauptmomente zur Bestimmung der Bemessungsmomente an den beiden Plattenseiten stellen sich somit wie folgt dar:

Sind die Hauptmomente für beide Plattenseiten bekannt, können die Bemessungsmomente bestimmt werden. Dazu werden in einem ersten Schritt die Differenzwinkel der Bewehrungsrichtungen zur Richtung des Hauptmoments an jeder Plattenseite ermittelt.

Der kleinste Differenzwinkel gibt den positiven Umfahrungssinn vor. Alle anderen Winkel werden in diesem positiven Umfahrungssinn ermittelt und anschließend der Größe nach sortiert. In RF-BETON Flächen erhalten sie wie in folgendem Beispiel dargestellt die Bezeichnungen α_m,+z, β_m,+z und γ_m,+z. Mit dem Index +z wird die Flächenunterseite gekennzeichnet.

Anschließend werden Gleichung 2.5 bis Gleichung 2.7 nach Baumann [1] verwendet, um die Bemessungsmomente zu bestimmen:

$$\begin{gathered} m_{\alpha } = m_l · \frac{\sin \beta · \sin \gamma + k · \cos \beta · \cos \gamma }{\sin (\beta - \alpha ) · \sin (\gamma - \alpha )} \\ {m}_{\beta } = m_l · \frac{\sin \alpha · \sin \gamma + k · \cos \alpha · \cos \gamma }{\sin (\beta - \alpha ) · \sin (\beta - \gamma )} \\ {m}_{\gamma } = m_l · \frac{-\sin \alpha · \sin \beta + k · \cos \alpha · \cos \beta }{\sin (\beta - \gamma ) · \sin (\gamma - \alpha )} \end{gathered}$$

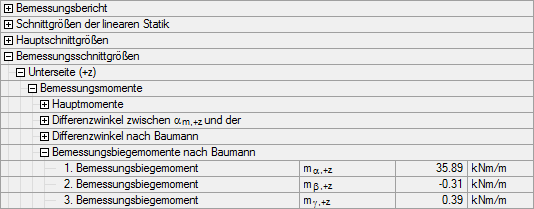
In RF-BETON Flächen werden die Bemessungsmomente m_α,+z, m_β,+z und m_γ,+z für die Plattenunterseite wie folgt ausgegeben:

In diesem Beispiel ist eines der Bemessungsmomente kleiner als Null. Es wird nun ein Bewehrungsnetz aus zwei Bewehrungslagen gesucht, das durch eine Betondruckstrebe ausgesteift wird.

Das erste angenommene Bewehrungsnetz besteht aus den beiden Bewehrungsscharen in die Richtungen α_m und β_m. Die Richtung γ der aussteifenden Betondruckstrebe (des aussteifenden, an dieser Plattenseite druckerzeugenden Moments) wird genau zwischen diesen Bewehrungsscharen angenommen.

${\gamma }_{1,am} = \frac{{\alpha }_m + {\beta }_m}{2}$

Es werden mit adaptierter Gleichung 2.5 bis Gleichung 2.7 erneut die Bemessungsmomente in den gewählten Bewehrungsscharen des Netzes und das sie aussteifende Moment bestimmt. Im Beispiel führt dies für die untere Plattenseite zur folgenden Ausgabe.

Die Annahme des Bewehrungsnetzes führt zu einer brauchbaren Lösung, da die Druckstrebenrichtung zulässig ist.

Die Analyse weiterer Druckstrebenrichtungen muss zeigen, ob es sich dabei um die energetisch kleinste Lösung mit dem geringsten Bewehrungsbedarf handelt. Diese Untersuchungen erfolgen analog.

Sind alle sinnvollen Möglichkeiten für ein Bewehrungsnetz aus zwei Bewehrungsscharen und einer aussteifenden Betondruckstrebe untersucht, werden die Summen der absoluten Bemessungsmomente bilanziert. Für das obige Beispiel sieht die Übersicht wie folgt aus.

Es wird die Kleinste Energie für alle zulässigen Fälle ∑_min,+z als minimale absolute Summe der ermittelten Bemessungsmomente angegeben. Im Beispiel liefert das Bewehrungsnetz aus den Bewehrungslagen für den Differenzwinkel β_m,+z,2a die günstigste Lösung für die untere Plattenseite.

Bei den Bemessungsdetails wird auch die Richtung der maßgebenden Druckstrebe angegeben. Diese Richtung bezieht sich auf die Definition der Differenzwinkel nach Baumann. Deshalb wird zusätzlich die Richtung φ_strebe bezogen auf die Bewehrungsrichtung ausgegeben. Im Beispiel wird für die untere Plattenseite folgender Druckstrebenwinkel ermittelt:

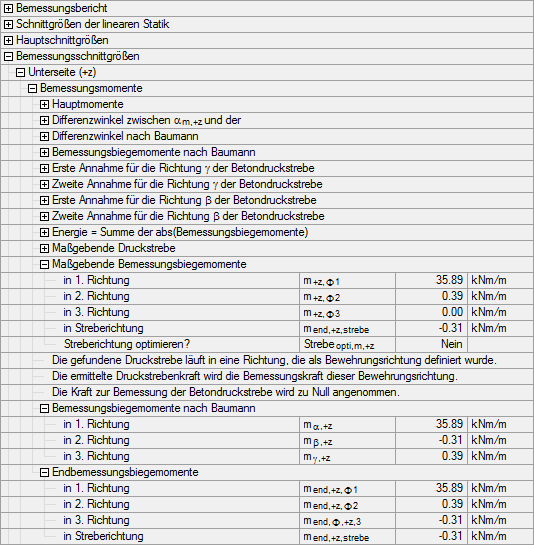
Bei optimierter Richtung des Bemessungsmoments, das das Bewehrungsnetz aussteift (siehe Bild 3.47), ergeben sich für obiges Beispiel die Bemessungsmomente nach Baumann. Diese Bemessungsmomente werden wie in folgendem Bild gezeigt auf die definierten Bewehrungsrichtungen übertragen.