Berücksichtigung von Schwinden
Als Schwinden wird eine zeitabhängige Änderung des Volumens ohne Einwirkung von äußeren Lasten oder Temperatur bezeichnet. Auf die weitere Verzweigung des Schwindproblems in einzelne Erscheinungsformen (Trocknungsschwinden, autogenes Schwinden, plastisches Schwinden und Karbonatisierungsschwinden) wird hier nicht näher eingegangen.
Wesentliche Einflussgrößen des Schwindens sind relative Luftfeuchte, wirksame Bauteildicke, Gesteinskörnung, Betonfestigkeit, Wasserzementwert, Temperatur sowie Art und Dauer der Nachbehandlung. Die Größe, durch die das Schwinden erfasst wird, ist die Gesamtschwinddehnung εcs zum betrachteten Zeitpunkt t.
Gemäß EN 1992-1-1, Abschnitt 3.1.4 setzt sich die Gesamtschwinddehnung εcs zusammen aus den Komponenten Trocknungsschwinden εcd und autogenes Schwinden εca:
εcs = εcd + εca
Gleichung 2.101 [7] Gl. (3.8)
Der Anteil aus Trocknungsschwinden εcd ermittelt sich wie folgt.
εcd(t) = βds(t,ts) · kh · εcd,0
Gleichung 2.102 [7] Gl. (3.9)
mit
|
t |
Betonalter zum betrachteten Zeitpunkt in Tagen |
|
ts |
Betonalter zu Beginn des Schwindens in Tagen |
|
h0 |
Wirksame Bauteildicke [mm] (bei Flächen: h0 = h) |
|
kh |
Koeffizient gemäß [4] Tabelle 3.3 in Abhängigkeit von der wirksamen Querschnittsdicke h0 |
|
εcd,0 |
Grundwert gemäß [4] Tabelle 3.2 oder Anhang B, Gl. (B.11) |
|
αds1, αds2 |
Beiwerte zur Berücksichtigung der Zementart (siehe Tabelle 2.3) |
|
fcm |
Mittlere Zylinderdruckfestigkeit des Betons in [N/mm2] |
|
fcmo |
= 10 N/mm2 |
| 32,5 N | S | Langsam erhärtend | 3 | 0,13 |
| 32,5 R; 42,5 R | N | Normal erhärtend | 4 | 0,12 |
| 42,5 R; 52,5 N/R | R | Schnell erhärtend | 6 | 0,11 |
Die autogene Schwinddehnung εca ermittelt sich wie folgt.
εca(t) = βas(t) · εca(∞) [7] Gl. (3.11)
mit
t - in Tagen
Erfassung des Schwindens in RF-BETON NL (mit Berücksichtigung der Bewehrung)
Die Angaben zur Schwinddehnung erfolgen in Maske 1.3 Flächen. Dort sind das Betonalter zum betrachteten Zeitpunkt und bei Schwindbeginn, die relative Luftfeuchte sowie der Zementtyp anzugeben. Aus diesen Vorgaben ermittelt RF-BETON NL dann die Schwinddehnung εcs.
Die Schwinddehnung εcs(t,ts) lässt sich auch normenunabhängig manuell vorgeben.
Die Schwinddehnung wird nur auf die Betonlayer angesetzt; die Bewehrungslayer bleiben unberücksichtigt. Somit besteht ein Unterschied zur klassischen Temperaturbelastung, die auch auf die Bewehrungslayer wirkt. Das in RF-BETON NL verwendete Modell für Schwinden berücksichtigt somit die Behinderung der Schwinddehnung εsh, die durch die Bewehrung oder die Querschnittsverkrümmung bei unsymmetrischer Bewehrung ausgeübt wird. Die resultierenden Lasten aus der Schwinddehnung werden automatisch als virtuelle Lasten auf die Flächen aufgebracht und berechnet. Je nach statischem System führt die Schwinddehnung zu zusätzlichen Spannungen (statisch unbestimmtes System) oder zusätzlichen Verformungen (statisch bestimmtes System). RF-BETON NL berücksichtigt den Einfluss der statischen Randbedingungen deshalb in unterschiedlicher Weise für den Ansatz des Schwindens.
Die aus Schwinden resultierenden Lasten werden automatisch der in Maske 1.1 Basisangaben definierten Belastung für Gebrauchstauglichkeit zugeordnet und gehen somit in die nichtlineare Berechnung ein.
Das Schwinden hängt von der korrekten Verteilung der Steifigkeit im Querschnitt ab. Daher ist für den Zugbereich des Betons die Berücksichtigung von Tension Stiffening (Betonrestzugfestigkeit nach Quast) und ein kleiner Wert für Dämpfung zu empfehlen.
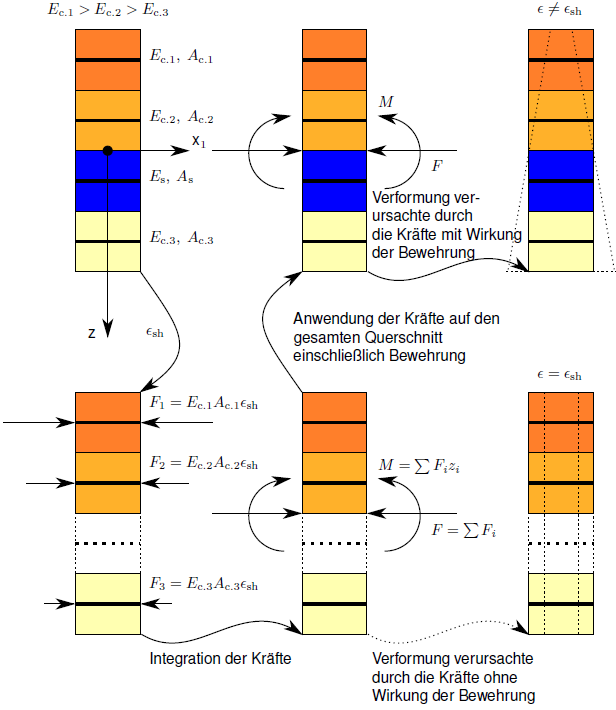
Das im Bild 2.148 dargestellte 1D-Modell veranschaulicht, wie das Schwinden im Programm erfasst wird.
Vereinfacht werden vier Schichten betrachtet: Die dunkelorangen Schichten repräsentieren den wenig beschädigten Beton, die hellorangen Schichten den stärker beschädigten Beton. Die blaue Schicht entspricht der Bewehrung. Jede Betonschicht wird mit dem tatsächlichen E-Modul Ec,i gekennzeichnet, jede Querschnittsfläche mit Ac,i. Die Bewehrung ist durch den tatsächlichen E-Modul Es und die Querschnittsfläche As charakterisiert. Jede Schicht ist anhand der Koordinate zi beschrieben.
Erfassung des Schwindens als äußere Last
Die Schwinddehnung kann auch in RFEM als äußere Last aufgebracht werden: Im RFEM-Dialog Neue Flächenlast ist über die links dargestellte Schaltfläche der Dialog Flächenlast infolge Schwinden generieren zugänglich.
In diesem Dialog können die Parameter zur Ermittlung der Schwinddehnung eingegeben werden. Mit [OK] wird das ermittelte Schwindmaß dann als Lastgröße in den Ausgangsdialog Neue Flächenlast übernommen. Die Lastart wird dabei automatisch auf Längenänderung gesetzt. Dabei ist zu beachten, dass die Schwinddehnung auf den gesamten Querschnitt wirkt und etwaige Behinderungen oder Querschnittsverkrümmungen durch die Bewehrung nicht berücksichtigt werden.
Literatur
[4] Quast, Ulrich. Zur Mitwirkung des Betons in der Zugzone. Beton und Stahlbetonbau, Heft 10, 1981.
[7] EN 1992-1-1: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken – Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2004