2.8.3.3 Versteifende Wirkung des Betons in Zugzone

Versteifende Wirkung des Betons in Zugzone

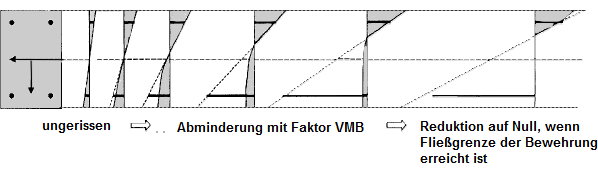
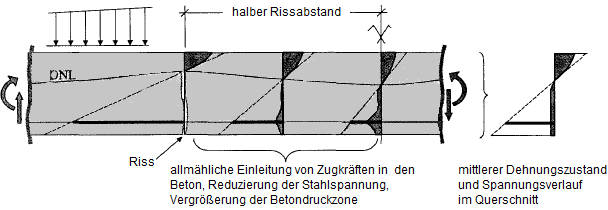
Bei gerissenen Stahlbetonteilen werden die Zugkräfte im Riss allein durch die Bewehrung aufgenommen. Zwischen zwei Rissen werden jedoch Zugspannungen über den (verschieblichen) Verbund in den Beton eingeleitet. Somit beteiligt sich der Beton an der Aufnahme innerer Zugkräfte, was zu einer Erhöhung der Steifigkeit des Bauteils führt. Dieser Effekt wird als versteifende Mitwirkung des Betons auf Zug zwischen den Rissen oder auch als Tension Stiffening bezeichnet.

Die Berücksichtigung einer Erhöhung der Bauteilsteifigkeit durch die Zugversteifung kann auf zwei Arten erfolgen:

• Es kann eine verbleibende, konstante Restzugspannung, welche nach der Rissbildung erhalten bleibt, in der Betonarbeitslinie involviert werden.

Die Restzugspannung ist dabei deutlich kleiner als die Zugfestigkeit des Betons. Alternativ können auch modifizierte Spannungs-Dehnungs-Beziehungen für den Zugbereich eingeführt werden, die über einen abfallenden Ast nach Erreichen der Zugfestigkeit das Mitwirken des Betons auf Zug zwischen den Rissen beachten.

• Eine weitere Variante stellt die Änderung der „nackten“ Arbeitslinie des Betonstahls dar.

Hierbei wird im betrachteten Querschnitt eine verringerte Stahldehnung ε_sm, die sich aus ε_s2 und einem Abzugsterm infolge der Zugversteifung ergibt, angesetzt.

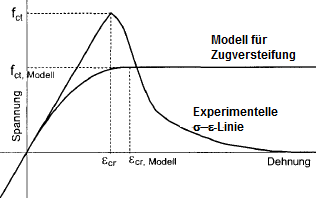
RF-BETON NL verwendet für die Berücksichtigung von Tension Stiffening den Ansatz über die Modellierung der Betonzugfestigkeit nach Quast [4]. Dieses Modell basiert auf einer definierten Spannungs-Dehnungs-Linie des Betons im Zugbereich (Parabel-Rechteck-Diagramm). Die grundlegenden Annahmen des Ansatzes von Quast können folgendermaßen zusammengefasst werden:

• Volle Mitwirkung des Betons auf Zug bis zum Erreichen der Rissdehnung ε_cr bzw. der rechnerischen Betonzugfestigkeit f_ct,R.
• Reduzierte versteifende Mitwirkung des Betons in der Zugzone entsprechend der vorhandenen Betondehnung
• Kein Ansatz von Tension Stiffening nach dem Einsetzen des Fließens des maßgebenden Bewehrungsstabes

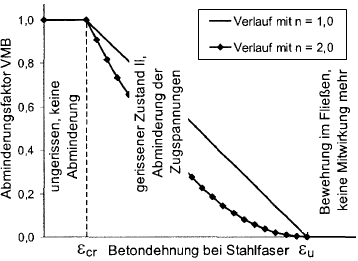
Zusammenfassend bedeutet dies, dass die rechnerische Zugfestigkeit f_ct,R keine fixe Größe ist, sondern sich auf die vorhandene Dehnung in der maßgebenden Stahl(zug)faser bezieht. Die maximale Zugfestigkeit f_ct,R nimmt ab der definierten Rissdehnung ε_cr bis zum Erreichen der Fließdehnung des Bewehrungsstahls in der maßgebenden Stahlfaser linear auf null ab. Erreicht wird dies durch die in Bild 2.137 gezeigte Spannungs-Dehnungs-Linie im Zugbereich des Betons (Parabel-Rechteck-Diagramm) und die Ermittlung eines Reduktionsfaktors VMB ( Versteifende Mitwirkung des Betons).

Die Spannungs-Dehnungslinie im Zugbereich kann mit folgenden Gleichungen beschrieben werden:

$$\begin{gathered} {\sigma }_c =\text{ VMB }· \left[f_{ct,R} · \left(1 - {\left(1 - \frac{\epsilon }{{\epsilon }_{cr}}\right)}^{n_{PR}}\right)\right] \text{ für} 0 < \epsilon < {\epsilon }_{cr} \\ {\sigma }_c =\text{ VMB} · f_{ct,R} \text{für} \epsilon > {\epsilon }_{cr } \text{(konstanter} \text{Verlauf}) \end{gathered}$$

Die Völligkeit der Parabel im ersten Abschnitt kann durch den Exponenten n_PR gesteuert werden. Der Exponent sollte so angepasst werden, dass der Übergang vom Druck- in den Zugbereich möglichst mit gleichem E-Modul erfolgt.

Zur Bestimmung des Reduktionsfaktors VMB wird die Dehnung an der am stärksten gezogenen Stahlfaser verwendet. Die Lage des Referenzpunkts ist in Bild 2.139 dargestellt.

Der Abminderungsfaktor VMB nimmt mit steigender Stahldehnung ab. Im Diagramm für den Faktor VMB (siehe Bild 2.140) ist ersichtlich, dass der Faktor VMB genau zum Fließbeginn der Bewehrung auf null reduziert wird.

Der Verlauf für den Abminderungsfaktor VMB im Zustand II (ε > ε_cr) kann über den Exponenten n_VMB gesteuert werden. Erfahrungswerte sind nach Pfeiffer [5] die Werte n_VMB = 1 (linear) bis n_VMB = 2 (Parabel) für biegebeanspruchte Bauteile. Quast [6] benutzt in seinem Modell den Exponenten n_VMB = 1(linear) und erzielt damit gute Übereinstimmungen bei der Nachrechnung von Stützenversuchen. Nach Pfeiffer [5] lassen sich mit n_VMB = 2 reine Zugversuche mit akzeptabler Übereinstimmung abbilden.

Die Annahme eines Parabel-Rechteck-Diagramms für die gerissene Betonzugzone ist als Rechenhilfe zu betrachten. Auf den ersten Blick bestehen große Unterschiede zu experimentell ermittelten Spannungs-Dehnungslinien auf der Zugseite des reinen Betons.

Bei der Betrachtung der vorhandenen Spannungen im biegebeanspruchten Stahlbetonquerschnitt zeigt sich, dass das Parabel-Rechteck-Diagramm durchaus besser in der Lage ist, die Dehnungen und Spannungen im Mittel zu beschreiben.

Bei einem Biegebalken bildet sich zwischen zwei Rissen ein Betonkörper. Dieser wirkt als eine Art Scheibe, in die durch die Bewehrung allmählich wieder Zugkräfte eingeleitet werden. Dadurch stellt sich ein sehr unregelmäßiger Verlauf von Spannung und Dehnung ein. Im Mittel lässt sich jedoch eine Dehnungsebene mit einem Parabel-Rechteck-Verlauf erstellen, durch den die mittlere Verkrümmung erfasst werden kann.

Die Höhe des anzusetzenden Rechenwertes für die Zugfestigkeit f_ct,R und die Rissdehnung ε_cr,R für das Modell von Quast hat dieser folgendermaßen vorgeschlagen.

$f_{ct,R} = \left|\frac{1}{20} · f_{cm}\right| {\epsilon }_{cr,R} = \left|\frac{1}{20} · {\epsilon }_{c1}\right|$

Der Rechenwert für die Zugfestigkeit f_ct,R ist somit kleiner als die Vorgaben des Eurocodes. Dies ist begründet durch die Beschreibung der Arbeitslinie und der Ermittlung des Reduktionsfaktors VMB, bei der die angenommene Zugspannung und die resultierende Zugkraft nach Überschreitung der Zugdehnung nur langsam abgemindert werden. Bei einer Dehnung von 2 ⋅ ε_cr ergibt sich noch eine wirkende Zugspannung von etwa 0.95 ⋅ f_ct,R. Damit kann bei Biegebeanspruchung die Reduzierung der Steifigkeit gut vorhergesagt werden. Bei einer reinen Zugbeanspruchung sind die o. g. Werte für f_ct,R zu gering. Hier sollten nach Pfeiffer [5] die Werte aus EC 2 für den Rechenwert der Zugfestigkeit angesetzt werden.

Die von Quast [6] empfohlenen Werte für f_ct,R = 1/20 ⋅ f_cm sind durch den Ansatz von 60 % der in EC 2 angegebenen Zugfestigkeiten zu erreichen. Bei dem Ansatz von f_ct,R = 0.6 ⋅ f_ctm wird einerseits das Aufreißen des Querschnittes zu früh vorhergesagt. Andererseits ist aber dadurch eine Reduktion der Zugfestigkeit unter Dauerlast (ca. 70 %) oder eine temporär höhere Last (z. B. das kurzzeitige Aufbringen der seltenen Einwirkungskombination), die zu einer geschädigten Zugzone führt, bereits berücksichtigt.

Die einzelnen Rechenwerte für die Zugzone des Betons lassen sich wie folgt beschreiben: