Considering Shrinkage

Considering Shrinkage

Shrinkage describes a time-dependent change of volume without the effect of external loads or temperature. This manual will not go into details regarding shrinkage problems and their individual types (drying shrinkage, autogenous shrinkage, plastic shrinkage, and carbonation shrinkage).
Significant influence values of shrinkage are relative humidity, effective thickness of structural components, aggregate, concrete strength, water-cement ratio, temperature, as well as the type and duration of curing. The shrinkage-determining value is the total shrinkage strain ε_cs at the considered point of time t.

According to EN 1992-1-1, Section 3.1.4, ([2] Eq. (3.8)), the total shrinkage strain ε_cs is composed of the components for drying shrinkage ε_cd and autogenous shrinkage ε_ca, as summarized in the equation below.

Drying Shrinkage

The component from drying shrinkage ε_cd is determined according to [2] Eq. (3.9) as follows.

where

• $${\mathrm{\beta }}_{\mathrm{ds}}(\mathrm{t}, {\mathrm{t}}_{\mathrm{s}}) =(\mathrm{t} - {\mathrm{t}}_{\mathrm{s}})/\left(\right(\mathrm{t} - {\mathrm{t}}_{\mathrm{s}}) + 0.4 · \sqrt{{{\mathrm{h}}_0}^3})$$

  t	Age of concrete at relevant point of time in days
  ts	Age of concrete when shrinkage starts in days
  h0	Effective thickness of the structural component [mm] (for surfaces: h0 = h)
  kh	Coefficient according to [1], Table 3.3, depending on the effective cross-section thickness h0
  εcd,0	Basic value according to [1] Table 3.2, or Annex B, Eq. (B.11)

  Factor β_ds (t,t_s)
• $${\mathrm{h}}_0 = \frac{2 · {\mathrm{A}}_{\mathrm{c}}}{\mathrm{u}}$$

  Ac	Cross-sectional area
  u	Cross-section perimeter

  Effective Thickness of Structural Component [mm] (for Surfaces: h₀ = h)
• $${\mathrm{\epsilon }}_{\mathrm{cd}, 0} = 0.85 · \left[(220 + 110 · {\mathrm{\alpha }}_{\mathrm{ds}1}) · \exp (-{\mathrm{\alpha }}_{\mathrm{ds}2} · \frac{{\mathrm{f}}_{\mathrm{cm}} }{{\mathrm{f}}_{\mathrm{cmo}} })\right] · {10}^{-6} · {\mathrm{\beta }}_{\mathrm{RH}}$$

  αds1, αds2	Factors for considering the type of cement
  fcm	Mean cylinder compressive strength of concrete in [N/mm²]
  fcmo	= 10 N/mm²

  Basic Value for Drying Shrinkage According to [1], Table 3.2, or Annex B, Eq. (B.11)
• $${\mathrm{\beta }}_{\mathrm{RH}} = 1.55 · \left[1 - \frac{\mathrm{R} {\mathrm{H}}^3}{\mathrm{R} {\mathrm{H}}_0}\right]$$

  RH	Relative humidity of environment [%]
  RH0	= 100%

  Formula β_RH

Autogenous Shrinkage Strain

The autogenous shrinkage strain ε_ca is determined according to [2] Eq. (3.11) as follows.

where

• $${\mathrm{\epsilon }}_{\mathrm{ca}}(\infty ) = 2.5 · ({\mathrm{f}}_{\mathrm{ck}} - 10) · {10}^{-6}$$

  Formula ε_ca(∞)
• $${\mathrm{\beta }}_{\mathrm{as}}\left(\mathrm{t}\right) = 1 - {\mathrm{e}}^{-0.2\sqrt{\mathrm{t}}}$$

  Formula β_as

Considering Shrinkage in Concrete Design (Taking Reinforcement into Account)

Specifications for the shrinkage strain are entered in the material dialog box in the Time-Dependent Properties of Concrete section. The age of concrete at the considered time and at the start of shrinkage, the relative humidity, and the cement type must be specified here. Based on these specifications, the program determines the shrinkage strain ε_cs.

The shrinkage strain ε_cs (t,t_s) can also be specified manually, independent of standards.
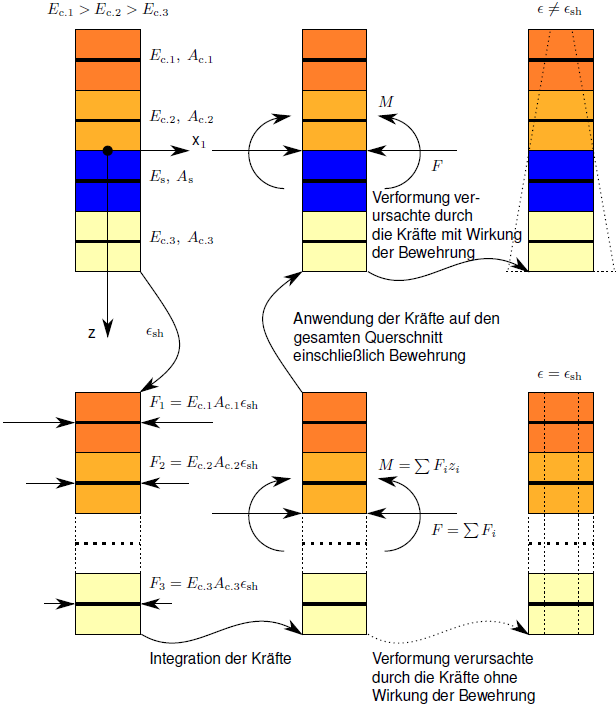
The shrinkage strain is only applied to the concrete layers; the reinforcement layers remain unconsidered. There is, therefore, a difference compared to the classical temperature loading, which also affects the reinforcement layers. Thus, the model for shrinkage used in the program considers the restraint of the shrinkage strain ε_sh that is exerted by the reinforcement or the cross-section curvature for an unsymmetrical reinforcement. The resulting loads from the shrinkage strain are automatically applied to the surfaces as virtual loads and calculated. Depending on the structural system, the shrinkage strain results in additional stresses (statically indeterminate system) or additional deformations (statically determinate system). Therefore, the program considers the influence of the structural boundary conditions in different ways for the shrinkage.

The shrinkage depends on the correct distribution of the stiffness in the cross-section. It is, therefore, recommended to take tension stiffening and a small value for damping into account for the tension areas of the concrete.
The 1D model in the image below illustrates how shrinkage is considered in the program.

Schematic Shrinkage Diagram in 1D Model

As a simplification, four layers are considered:

• The dark orange layers represent the concrete with little damage,
• the light orange layers represent the more heavily damaged concrete.
• The blue layer corresponds to the reinforcement.
• Each concrete layer is characterized by the actual modulus of elasticity E_c,i and each cross-sectional area by A_c,i.
• The reinforcement is characterized by the actual modulus of elasticity E_s and the cross-sectional area A_s.
• Each layer is described by means of the coordinate z_i.