Concrete Tensile Strength Modified According to Quast and Quast

Quast

This model that is used to determine the effectiveness of concrete on tension between cracks is based on a defined stress-strain curve of concrete in the tension zone (parabola-rectangle diagram).

The basic assumptions of Quast's approach can be summarized as follows:

• Full contribution of the concrete to tension until reaching the crack strain ε_cr or the calculational concrete tensile strength f_ct,R
• Reduced stiffening contribution of the concrete in the tension zone according to the existing concrete strain
• No application of tension stiffening after the governing rebar starts yielding

To sum up, this means that the tensile strength f_ct,R used for the calculation is not a fixed value, but relates to the existing strain in the governing steel (tension) fiber. The maximum tensile strength f_ct,R decreases linearly to zero, starting at the defined crack strain ε_cr until reaching the yield strain of the reinforcing steel in the governing steel fiber.
This can be achieved by the stress-strain relation in the tension area of the concrete (parabola-rectangle diagram), shown in the following image, and the determination of a reduction factor VMB (stiffening contribution of concrete).

Stress-Strain Diagram of Concrete in Tension with Reduction Factor VMB = 0.4

The next image shows a schematic view of stress states for increasing loading due to tension stiffening.

Stress States for Increasing Loads with Tension Stiffening

The stress-strain relation in the tension zone can be described with the following equations:

• The curvature of the parabola in the first section can be controlled by the exponent n_PR.
• The exponent should be adjusted in such a way that the transition from the compression zone to the tension zone is preferably achieved with the same modulus of elasticity.

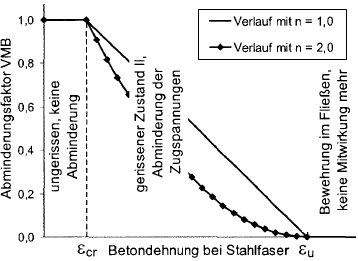
To determine the reduction factor VMB, the strain at the most tensioned steel fiber is used. The position of the reference point is illustrated in the graphic below.

Determination of Residual Tensile Strength for Tension Stiffening According to Quast

The reduction parameter VMB decreases with increasing steel strain. In the diagram for the VMB factor (see the image below), it is evident that the factor VMB is reduced to zero exactly at the point when the yielding of the reinforcement starts.

Reduction Factor VMB – Tension Stiffening According to Quast

The distribution for the reduction factor VMB in state II (ε > ε_cr) can be controlled by means of the exponent n_VMB.

• According to Pfeiffer [2], the values n_VMB = 1 (linear) to n_VMB = 2 (parabola) are experiential values for structural components subjected to bending.
• Quast [3] uses the exponent n_VMB = 1 (linear) in his model, thus achieving good concordance when recalculating column tests.
• According to Pfeiffer [2], it is possible to describe pure tension tests with acceptable concordance by using n_VMB = 2.

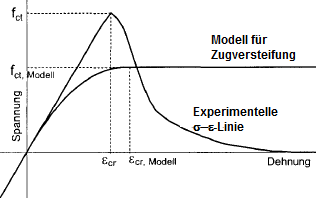
The assumption of a parabola-rectangle diagram for the cracked concrete tension zone can be regarded as a calculation aid. At first glance, there are great differences compared to the experimentally determined stress-strain diagrams on the tension side of the pure concrete.

Tension Stiffening According to Quast – Comparison of Model and Lab Test

The given stresses in the reinforced concrete cross-section in bending show that the parabola-rectangle diagram is indeed better suited to describe the mean of the strains and stresses.
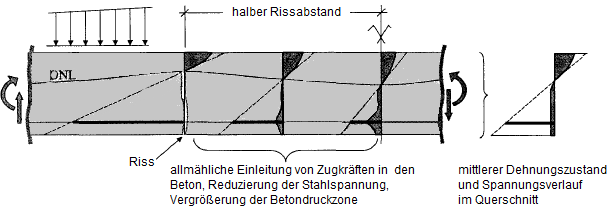
In a bending beam, a concrete body forms between two cracks. It acts as a sort of wall into which tension forces are gradually reintroduced by the reinforcement. This results in a very irregular distribution of stress and strain. On average, however, we can create a plane of strain with a parabola-rectangle distribution with which it is possible to consider the mean curvature.

Existing Stress State for Reinforced Concrete Under Bending

For the model by Quast, the calculation values to be applied were proposed as follows:

• For the tensile strength f_ct,R

• For the crack strain ε_cr,R

The calculational value for the tensile strength f_ct,R is thus smaller than specified by the Eurocode. This is due to the description of the stress-strain relation and the determination of the reduction parameter VMB, in which the assumed tension stress and the resulting tension force are only slowly reduced after exceeding the tension strain. For a strain of 2 ⋅ ε_cr, there is also an acting tension stress of about 0.95 ⋅ f_ct,R. Thus, in case of bending, the reduction of the stiffness can be predicted well. For pure tension, the above-mentioned values for f_ct,R are too small. According to Pfeiffer [2], the values from EC 2 should be applied for the calculation value of the tensile strength.
The values for f_ct,R = 1/20 ⋅ f_cm recommended by Quast [3] can be reached by applying 60 % of the tensile strengths given in EC 2. On the one hand, the cracking of the cross-section is predicted too early when applying f_ct,R = 0.6 ⋅ fctm. On the other hand, this already takes into account a reduction of the tensile strength under permanent load (about 70 %) or a temporarily higher load (e.g. the short-term application of the rare action combination) that results in a damaged tension zone.
The individual calculation values for the concrete's tension zone can be described as follows:

Modified Approach According to Quast