TS modificato secondo Quast e Quast

Quast

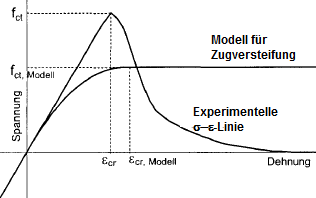
Questo modello per determinare il contributo del calcestruzzo alla trazione tra le fessure si basa su una curva tensione-deformazione definita del calcestruzzo nell'area di trazione (diagramma parabola-rettangolo).

Le ipotesi di base dell'approccio di Quast possono essere riassunte come segue:

• Contributo completo del calcestruzzo in trazione fino al raggiungimento della deformazione della fessura ε_cr o della resistenza a trazione del calcestruzzo fattorizzato f_ct,R .
• Contributo di irrigidimento ridotto del calcestruzzo nella zona di trazione in base alla deformazione del calcestruzzo esistente
• Nessun irrigidimento a trazione dopo che l'armatura determinante ha iniziato a snervarsi

In sintesi, ciò significa che la resistenza a trazione fattorizzata f_ct,R non è un valore fisso, ma si riferisce alla deformazione esistente nella fibra di acciaio determinante (trazione). La resistenza a trazione massima f_ct,R diminuisce linearmente a zero dalla deformazione della fessura definita ε_cr fino a quando non viene raggiunta la deformazione di snervamento dell'acciaio di armatura nella fibra di acciaio determinante.
Ciò si ottiene utilizzando la relazione tensione-deformazione nell'area di trazione del calcestruzzo (diagramma parabola-rettangolo), mostrata nell'immagine seguente e determinando un coefficiente di riduzione VMB (contributo di irrigidimento del calcestruzzo).

Curva tensione-deformazione del calcestruzzo in trazione con fattore di riduzione VMB = 0,4

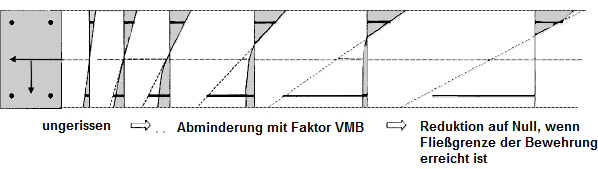
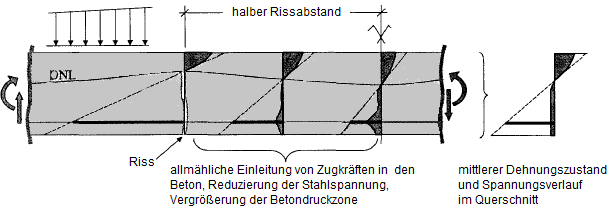
L'immagine successiva mostra una vista schematica degli stati di tensione per l'aumento del carico dovuto all'irrigidimento a trazione.

Stato di tensione per carico crescente con tension stiffening

La relazione tensione-deformazione nella zona di trazione può essere descritta con le seguenti equazioni:

• La curvatura della parabola nella prima sezione può essere controllata dall'esponente n_PR.
• L'esponente dovrebbe essere regolato in modo tale che la transizione dalla zona di compressione alla zona di trazione sia preferibilmente ottenuta con lo stesso modulo di elasticità.

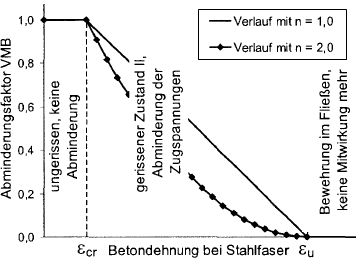
Per determinare il coefficiente di riduzione VMB, viene utilizzata la deformazione della fibra di acciaio più tesa. La posizione del punto di riferimento è illustrata nel grafico seguente.

Determinazione della resistenza residua a trazione per irrigidimento a trazione secondo Quast

Il parametro di riduzione VMB diminuisce con l'aumentare della deformazione dell'acciaio. Nel diagramma per il coefficiente VMB (vedi immagine sotto), è evidente che il coefficiente VMB è ridotto a zero esattamente nel punto in cui inizia lo snervamento dell'armatura.

Fattore di riduzione VMB - Irrigidimento a trazione secondo Quast

La distribuzione per il coefficiente di riduzione VMB nello stato II (ε > ε_cr ) può essere controllata mediante l'esponente n_VMB.

• Secondo Pfeiffer [2], i valori da n_VMB = 1 (lineare) a n_VMB = 2 (parabola) sono valori sperimentali per componenti strutturali soggetti a flessione.
• Quast [3] utilizza l'esponente n_VMB = 1 (lineare) nel suo modello, ottenendo così una buona concordanza durante il ricalcolo dei test delle colonne.
• Secondo Pfeiffer [2], le prove di trazione pura con conformità accettabile possono essere modellate con n_VMB = 2.

L'ipotesi di un diagramma parabola-rettangolare per la zona tesa del calcestruzzo fessurato deve essere considerata come un ausilio per il calcolo. A prima vista, ci sono grandi differenze rispetto alle curve tensione-deformazione determinate sperimentalmente sul lato teso del calcestruzzo puro.

Tension Stiffening secondo Quast – Confronto tra modello e test di laboratorio

Le tensioni date nella sezione trasversale in cemento armato in flessione mostrano che il diagramma parabola-rettangolo è effettivamente più adatto per descrivere la media delle deformazioni e delle tensioni.
In una trave flettente, si forma un corpo di calcestruzzo tra due fessure. Agisce come una sorta di muro in cui le forze di trazione vengono gradualmente reintrodotte dall'armatura. Ciò si traduce in una distribuzione molto irregolare di tensione e deformazione. In media, tuttavia, è possibile creare un livello di deformazione con una curva parabola-rettangolare, attraverso la quale è possibile determinare la curvatura media.

Stato tensionale esistente del calcestruzzo armato in flessione

Per il modello di Quast, i valori di calcolo da applicare sono stati proposti come segue:

• Per la resistenza a trazione f_ct,R

• Per la deformazione della fessura ε_cr,R

Il valore di calcolo per la resistenza a trazione f_ct,R è quindi inferiore a quanto specificato dall'Eurocodice. Ciò è dovuto alla descrizione della relazione tensione-deformazione e alla determinazione del parametro di riduzione VMB, in cui la tensione di trazione presunta e la forza di trazione risultante vengono ridotte solo lentamente dopo aver superato la deformazione a trazione. Per una deformazione di 2 ⋅ ε_cr, c'è anche una tensione di trazione agente di circa 0,95 ⋅ f_ct,R. Pertanto, in caso di flessione, la riduzione della rigidezza può essere ben prevista. Per la trazione pura, i valori sopra menzionati per f_ct,R sono troppo piccoli. Secondo Pfeiffer [2], i valori di EC 2 dovrebbero essere applicati per il valore di calcolo della resistenza a trazione.
I valori consigliati da Quast [3] per f_ct,R = 1/20 ⋅ f_cm possono essere ottenuti applicando il 60% delle resistenze a trazione fornite in EC 2. Quando si applica f_{ct ,R} = 0.6 ⋅ fctm, si prevede che la sezione trasversale si fessura troppo presto. Allo stesso tempo, questo tiene già conto di una riduzione della resistenza a trazione sotto carico permanente (circa 70%) o di un carico temporaneamente più alto (ad esempio l'applicazione a breve termine della rara combinazione di azioni) che porta a una zona di trazione danneggiata.
I singoli valori di calcolo per la zona di trazione del calcestruzzo's possono essere descritti come segue:

Approccio modificato secondo Quast