Manuali online RFEM 6 / RSTAB 9 | Verifica calcestruzzo

Torna a Manuali online

Questa pagina ti è stata utile?

60x

005923

Dipl.-Ing. Juliane Stopper-Akdag

2025-01-21

Seleziona il manuale

Panoramica

Add-on per la verifica di strutture in calcestruzzo

Resistenza a trazione del calcestruzzo modificata secondo Quast e Quast

Basi teoriche

Analisi non-lineare

Specifiche di analisi

Specifiche di progetto

Stato limite di esercizio

Controllo dell'inflessione
- Analisi degli spostamenti generalizzati diretti

progettazione

Risultati

Documentazione

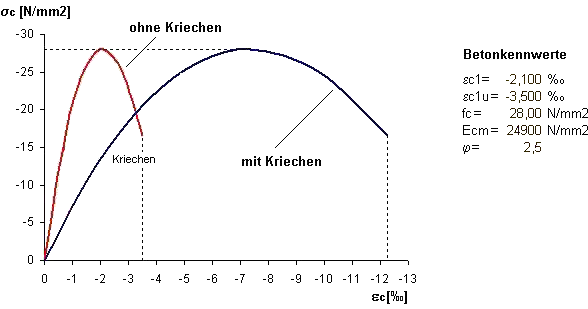
Considerando la viscosità

La viscosità descrive la deformazione del calcestruzzo dipendente dal tempo con il carico entro un particolare periodo di tempo. I valori di influenza essenziale sono simili a quelli del ritiro. Inoltre, la cosiddetta "tensione che produce viscosità" ha un effetto considerevole sulle deformazioni viscose.

È necessario prestare attenzione alla durata del carico, al tempo di applicazione del carico e all'entità del carico. La viscosità è presa in considerazione dal coefficiente di viscosità φ(t,t₀ ) nel momento t.

È possibile attivare la viscosità nella finestra di dialogo del materiale nella sezione Proprietà dipendenti dal tempo del calcestruzzo. Qui, è possibile specificare l'età del calcestruzzo nel momento considerato e all'inizio del carico, l'umidità relativa dell'aria e il tipo di cemento. Sulla base di queste specifiche, il programma determina il coefficiente di viscosità φ.

Determinazione del coefficiente di viscosità

Ora vedremo brevemente la determinazione del coefficiente di viscosità φ secondo EN 1992-1-1, punto 3.1.4. L'utilizzo delle seguenti equazioni richiede che la tensione di produzione di viscosità σ_c del carico permanente agente non superi il valore seguente.

σ_c ≤ 0,45 · f_ckj
dove
f_ckj - resistenza a compressione cilindrica del calcestruzzo nel momento in cui viene applicata la tensione che produce la viscosità

Diagramma delle tensioni σc e delle deformazioni del materiale nel tempo

Tensione di scorrimento σc

Assumendo un comportamento viscoso lineare (σ_c << 0.45 ⋅ f_ckj ), la viscosità del calcestruzzo' può essere determinata da una riduzione del modulo di elasticità del calcestruzzo's.

E_{c, eff} = \frac{E_{cm}}{1.0 + φ (t, t_{0})}

E_cm	Modulo di elasticità medio secondo EN 1992-1-1, Tabella 3.1
φ(t,t₀)	Coefficiente di viscosità
t	Età del calcestruzzo nel momento rilevante in giorni
t₀	Età del calcestruzzo quando inizia l'applicazione del carico in giorni

Viscosità del calcestruzzo

Secondo EN 1992-1-1, punto 3.1.4, il coefficiente di viscosità φ(t,t₀ ) nel momento analizzato t può essere calcolato come segue.

ϕ (t, t_{0}) = ϕ_{RH} \cdot β (f_{cm}) \cdot β (t_{0}) \cdot β (t, t_{0})

β(f_cm)	coefficiente per considerare la resistenza a compressione del calcestruzzo
β(t₀)	coefficiente per considerare l'età del calcestruzzo

Il coefficiente di viscosità φ(t,t₀ ) nel punto di tempo analizzato t

β (f_{cm}) = \frac{16 . 8}{\sqrt{f_{cm}}}

Coefficiente per considerare la resistenza a compressione del calcestruzzo

β (t_{0}) = \frac{1}{0.1 + {t_{0 . eff}}^{0.2}}

coefficiente per considerare l'età del calcestruzzo

φ_{RH} = 1 + \frac{1 - \frac{RH}{100}}{0.10 \cdot \sqrt[3]{h_{0}}} \cdot α_{1} \cdot α_{2}

h₀	Spessore efficace del componente strutturale [mm] (per superfici: h₀ = h)
α₁	coefficiente di adattamento
α₂	Anpassungsfaktor

Formula_φUR

h_{0} = \frac{2 \cdot A_{c}}{u}

A_c	area della sezione trasversale
u	Perimetro della sezione trasversale

Spessore efficace del componente strutturale [mm] (per superfici: h₀ = h)

α_{1} = {(\frac{35}{f_{cm}})}^{0.7}

f_cm	Resistenza a compressione cilindrica media

Coefficiente di correzione α₁

α_{2} = {(\frac{35}{f_{cm}})}^{0.2}

f_cm	Resistenza a compressione cilindrica media

Coefficiente di correzione α₂

t_{0 . eff} = t_{0} {[1 + \frac{9}{2 + {t_{0}}^{1.2}}]}^{α} \geq 0.5 \cdot d

Formel t_0.eff

β (t, t_{0}) = {[\frac{t - t_{0}}{β_{H} + t - t_{0}}]}^{0.3}

t	Età del calcestruzzo nel momento rilevante in giorni
t₀	Betonalter zu Belastungsbeginn in Tagen

Coefficiente per tener conto della durata del carico

β_{H} = 1.5 \cdot {[1 + {(0.012 \cdot RH)}^{18}]}^{α} \cdot h_{0} + 250 \cdot α_{3} \leq 1500 \cdot α_{3}

RH	umidità relativa [%]
h₀	spessore efficace del componente [mm]
α₃	coefficiente di adattamento

Formula β_H

α_{3} = {(\frac{35}{f_{cm}})}^{0.5}

f_cm	Valore medio della resistenza a compressione del cilindro

Coefficiente di correzione α_3°

L'influenza del tipo di cemento sul coefficiente di viscosità del calcestruzzo' può essere presa in considerazione modificando l'età di applicazione del carico t₀ con la seguente equazione:

t_{0} = t_{0, T} \cdot {(1 + \frac{9}{2 + {(t_{0, T})}^{1.2}})}^{α} \geq 0.5

t₀, t_T

età efficace del calcestruzzo quando inizia l'applicazione del carico, tenendo conto dell'influenza della temperatura

esponente a seconda del tipo di cemento:

-1 : cementi a indurimento lento (S) (32,5)
0 : cementi a indurimento normale o rapido (N) (32.5 R; 42.5)
1 : cementi ad alta resistenza a rapido indurimento (R) (42.5 R; 52.5)

Età del carico t₀

Considerando la viscosità nel calcolo

Se sono note le deformazioni nel momento t = 0 e in un momento successivo t, è possibile determinare il coefficiente di viscosità φ per una considerazione di calcolo nel modello.

φ_{t} = \frac{ε_{t}}{ε_{t = 0}} - 1

Coefficiente di viscosità

Questa equazione è riorganizzata alla deformazione nel punto di tempo t. Quindi, otteniamo la seguente relazione, che è valida per tensioni uniformi:

ε_{t} = ε_{t = 0} \cdot (φ_{t} + 1)

relazione che è valida per tensioni uniformi

Per tensioni superiori a circa 0.4 ⋅ f_ck, le deformazioni aumentano in modo sproporzionato, con conseguente perdita del riferimento linearmente assunto.

Il calcolo utilizza la soluzione consentita per scopi pratici di costruzione secondo EN 1992-1-1, 5.8.6 (3). Il diagramma tensione-deformazione del calcestruzzo è distorto dal coefficiente (1 + φ).

Linea tensione-deformazione nel cemento armato per rilevare l'effetto del creep

Deformazione della curva tensione-deformazione nel calcestruzzo armato

Quando si tiene conto della viscosità, si presuppongono tensioni che producono viscosità uniformi durante il periodo di applicazione del carico, come si può vedere nella figura sopra. A causa delle ridistribuzioni delle tensioni trascurate, la deformazione è leggermente sovrastimata a causa di questa ipotesi. La riduzione della tensione senza una variazione della deformazione (rilassamento) è presa in considerazione solo in misura limitata in questo modello. Se assumiamo un comportamento elastico lineare, si potrebbe presumere una proporzionalità e la distorsione orizzontale rifletterebbe anche il rilassamento con un rapporto di (1 + φ). Questa correlazione, tuttavia, è persa per la relazione non lineare tensione-deformazione.

Quindi, diventa chiaro che questa procedura deve essere intesa come un'approssimazione. Pertanto, una riduzione delle tensioni dovute al rilassamento e alla viscosità non lineare non può essere rappresentata o può essere rappresentata solo approssimativamente.

Capitolo principale

Comportamento dipendente dal tempo - viscosità e ritiro