混凝土抗拉强度按照规范和规范调整后

Quast

该模型基于裂缝间混凝土受拉区定义的应力-应变曲线（抛物线-矩形图），

Quast'的方法的基本假设可以总结如下：

• 混凝土在达到裂缝应变 ε_cr或计算抗拉强度 f_{ct,R 之前}的全部受拉作用。
• 根据现有的混凝土应变，受拉区混凝土刚度的折减。
• 在主导钢筋开始屈服后不应用受拉刚化。

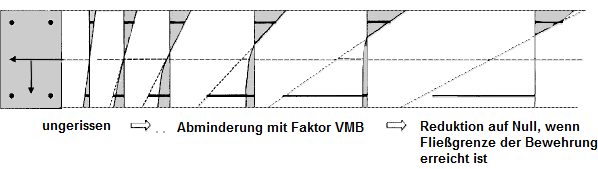
总之，这意味着用于计算的抗拉强度 f_ct，R不是一个固定值，而是与主导钢筋中存在的应变（受拉）有关。 主导钢筋中的最大抗拉强度 f_ct,R从定义的裂缝应变 ε_cr开始，直到达到主导钢筋的屈服应变为止，线性下降到零。
这可以通过下图所示的混凝土受拉区域的应力-应变图（抛物线-矩形图）并确定折减系数 VMB（混凝土的刚度贡献）来实现。

混凝土受拉区应力-应变曲线，减少系数 VMB = 0.4

下图显示了由于受拉刚化，增加荷载的应力状态视图。

考虑张力增强效果的应力状态

在受拉区的应力-应变曲线可以用下面的公式来描述：

• 抛物线在第一截面中的曲率可以通过指数 n_PR控制。
• 调整指数时，应考虑轴心受压区到受拉区的过渡区具有相同的弹性模量。

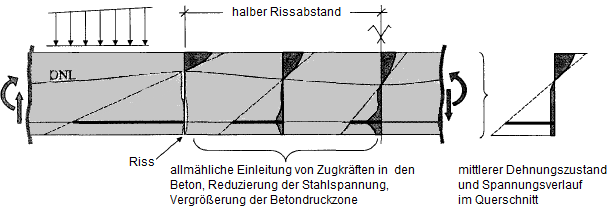
为了确定折减系数VMB，使用受拉最大的钢纤维处的应变。 下图显示了参考点的位置。

采用 Quast 方法确定拉伸硬化余抗

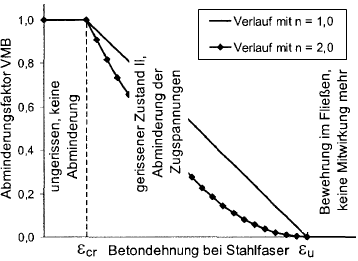
折减参数 VMB 随着钢筋应变的增加而减小。 在系数VMB 的图中（见下图）可以看出，在配筋开始屈服的那一点，系数VMB 减小为零。

下降系数 VMB – 拉伸刚度

在状态 II (ε >_cr ) 中折减系数 VMB 的分布可以通过指数 n_VMB控制。

• 根据规范 Pfeiffer]，n_VMB = 1（线性）至 n_VMB = 2（抛物线）的数值是指结构构件在受弯时的经验值。
• Quast [3] 在其模型中使用指数 n_VMB = 1（线性），从而在重新计算柱测试时获得良好的一致性。
• 根据 Pfeiffer {%于#参照 [2]]]，通过 n_VMB = 2 来描述纯拉力试验，并且一致性可以接受。

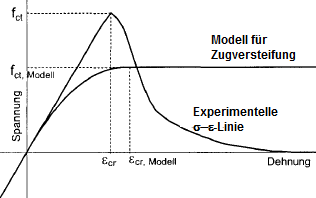
为了辅助计算， 乍一看，在受拉一侧的纯混凝土与实验确定的应力-应变图存在很大差异。

Quast 的受拉约束效应 - 模型与实验室试验比较

给出的钢筋混凝土截面受弯截面的应力表明，抛物线-矩形图更适合于描述应变的平均值和应力的平均值。
在受弯的梁中，两个裂缝之间形成混凝土主体。 它的作用类似于墙体，拉力会通过钢筋逐渐重新导入。 这会导致应力和应变的分布非常不规则。 一般情况下，我们可以创建一个呈抛物线-矩形分布的应变平面，通过它可以考虑平均曲率。

钢筋混凝土受弯的现有应力状态

对于Quast的模型，建议使用的计算值如下

• 抗拉强度 f_ct,R

• ε_cr,R用于裂缝应变

因此，抗拉强度的计算值 f_ct,R小于欧洲规范中规定的值。 这是由于应力-应变关系的描述和折减参数 VMB 的确定，其中假设的拉应力和合成拉力在超过拉应变后只会缓慢地减少。 对于应变 2 ⋅ ε_cr ，相应的拉应力作用为0.95 ⋅ f_ct,R 。 这样可以很好地预测构件受弯时的刚度折减。 对于纯受拉情况，上述的 f_ct,R数值过小。 #参见[2]]]时，抗拉强度的计算采用EC 2中的数值。
_Quast {%_！ ，当应用 f_ct,R = 0.6 ⋅ fctm 时，过早预测截面开裂。 另一方面，这已经考虑到在永久荷载作用下抗拉强度的降低（约 70 %）或暂时较高的荷载（例如短期内罕遇作用组合）会导致受拉区受损。
混凝土'受拉区的各个计算值如下：

根据 Quast 的修正方法