16190x

001513

Dipl.-Ing. (FH) Lukas Sühnel

2018-04-04

Pipes Under Internal Pressure Load

Piping systems are exposed to a variety of loads. One of the most decisive is internal pressure. This article will, therefore, deal with the stresses and deformations resulting from a pure internal compression load in the pipe wall or for the pipe.

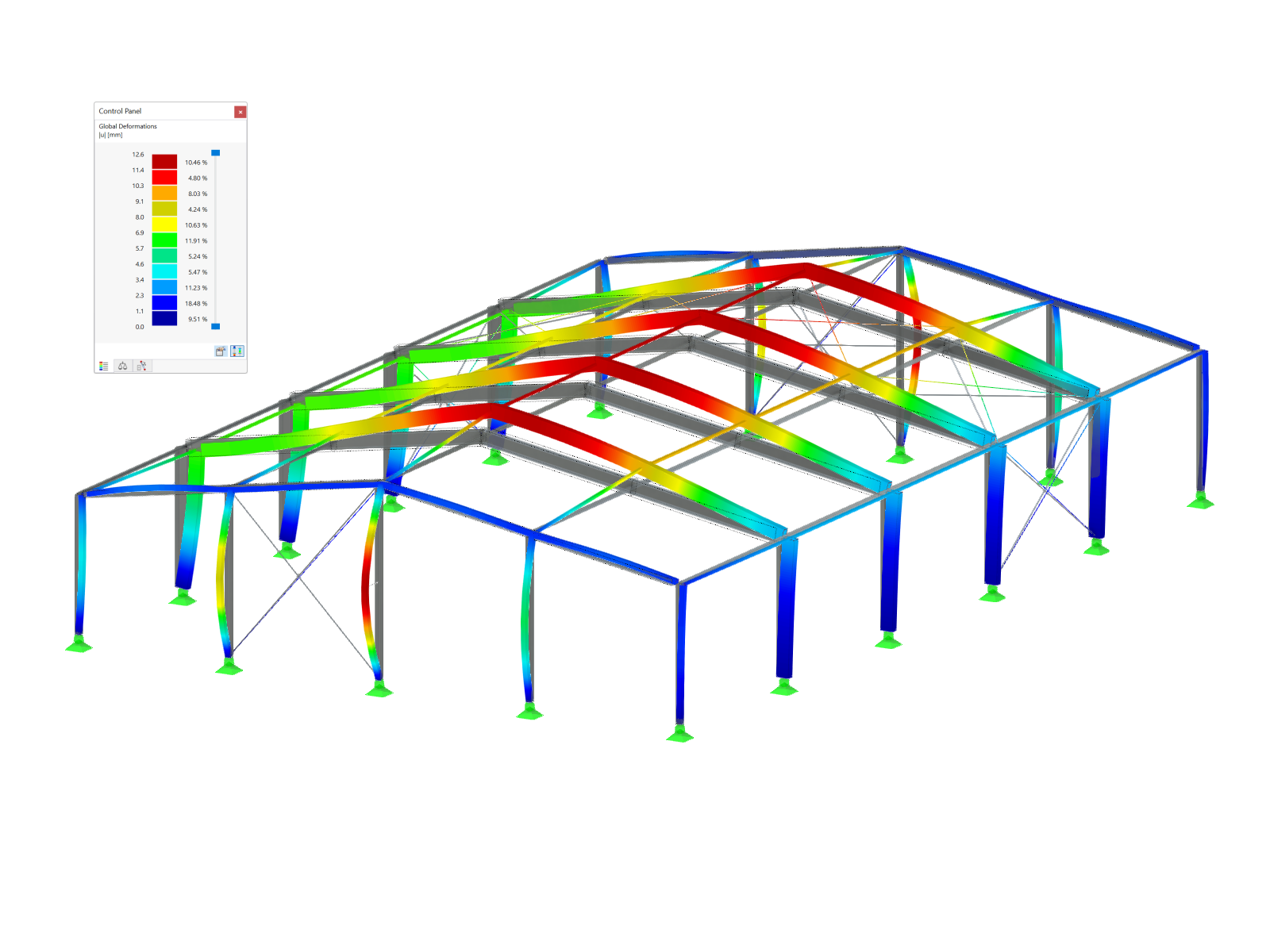
For the sake of traceability, the following example is used.

System

The tube is considered to be closed on both sides. As a result, on one hand, pressure is exerted perpendicular to the inner "lid surface".

Längsspannung

The resulting force must, in turn, be absorbed by the pipe wall. This results in longitudinal stress that can be calculated as follows:

σ_{l} = \frac{P \cdot r_{i}^{2}}{r_{e}^{2} - r_{i}^{2}}

Formula 1

where
r_i, r_e = inner and outer radius

On the other hand, the internal pressure acts perpendicular to the pipe's inner wall. This results in tangential and radial stress that can be determined by the following formulas:

σ_{t} = P \cdot \frac{{(\frac{r_{e}}{r})}^{2} 1}{{(\frac{r_{e}}{r_{i}})}^{2} - 1}

Formula 2

σ_{r} = - P \cdot \frac{{(\frac{r_{e}}{r})}^{2} - 1}{{(\frac{r_{e}}{r_{i}})}^{2} - 1}

Formula 3

where
r = radius in the limits r_i ≤ r ≤ r_e

It can be seen that the stresses depend on the considered radius r. This implies, conversely, that these run unevenly across the cross-section. For thin-walled tubes (outer diameter/inner diameter < 1.2), however, uniform stress distribution can be assumed. This results in the mean tangential or radial stress to:

\begin{array}{l} {\bar{σ}}_{t} = \frac{P \cdot r_{i}}{r_{e} - r_{i}} \\ {\bar{σ}}_{r} = \frac{P \cdot r_{i}}{r_{e} r_{i}} \end{array}

Formula 4

Inserting the input values into the formulas results in the following stresses:

\begin{array}{l} σ_{l} = \frac{2 \cdot 103 . 25^{2}}{109 . 55^{2} - 103 . 25^{2}} = 15.9 N / mm ² \\ {\bar{σ}}_{t} = \frac{2 \cdot 103.25}{109.55 - 103.25} = 32.8 N / mm ² \\ {\bar{σ}}_{r} = \frac{- 2 \cdot 103.25}{109.55 103.25} = - 1, 0 N / mm ² \end{array}

Formula 5

The internal pressure also results in a change in the length of the pipe. In general terms, the change in length is equal to the product of the length with the strain epsilon:
ΔL = L ∙ ε

The strain of the pipe results from the three stresses just calculated:

ε = \frac{(σ_{l} - v \cdot (σ_{t} σ_{r}))}{E} = \frac{(15.9 - 0.3 \cdot (32.8 - 1))}{212, 000} = 3 \cdot 10^{- 5}

Formula 6

The change in length is therefore:
ΔL = 10,000 mm ∙ 3 ∙ 10 ^-5 = 0.3 mm

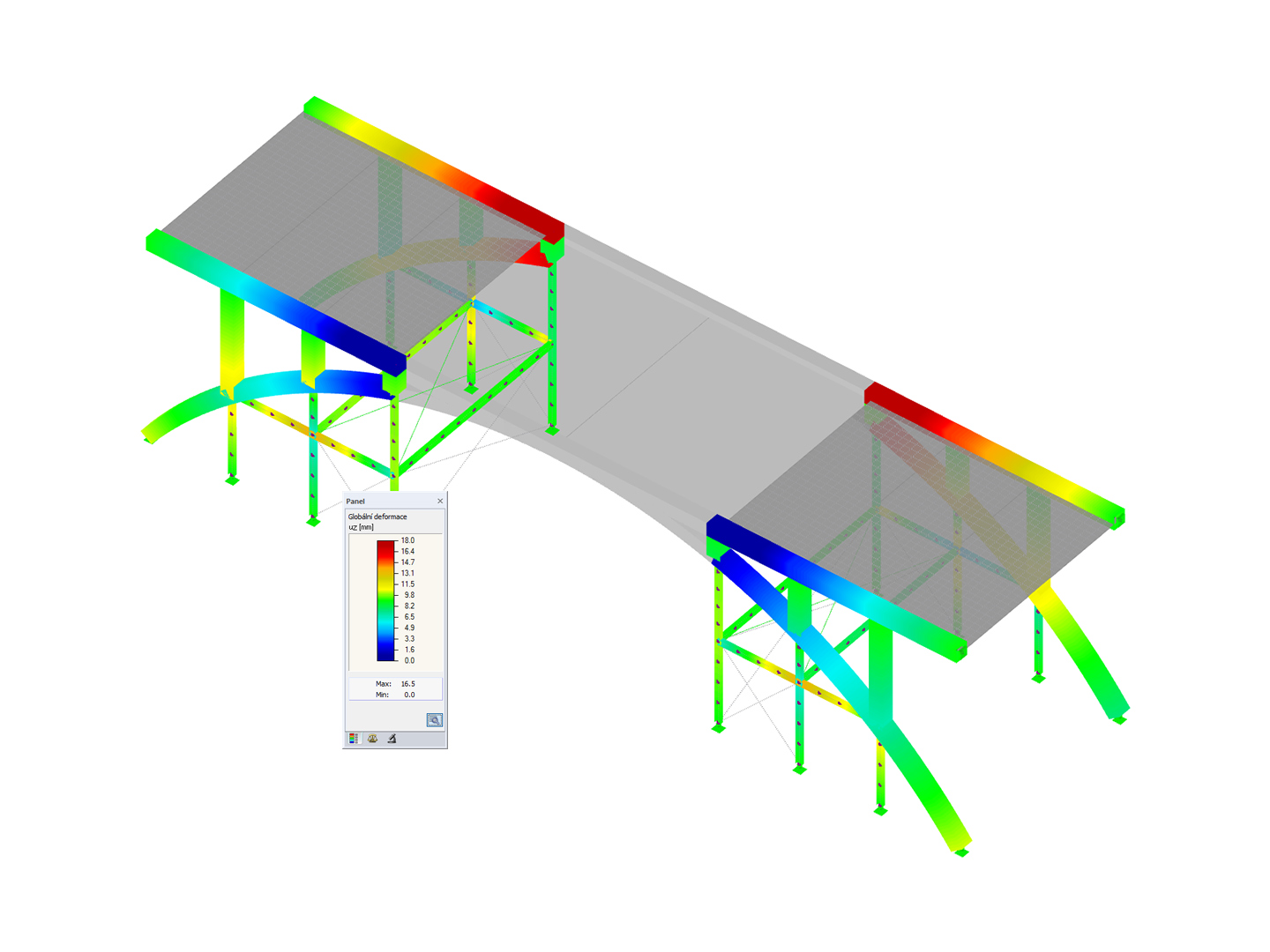
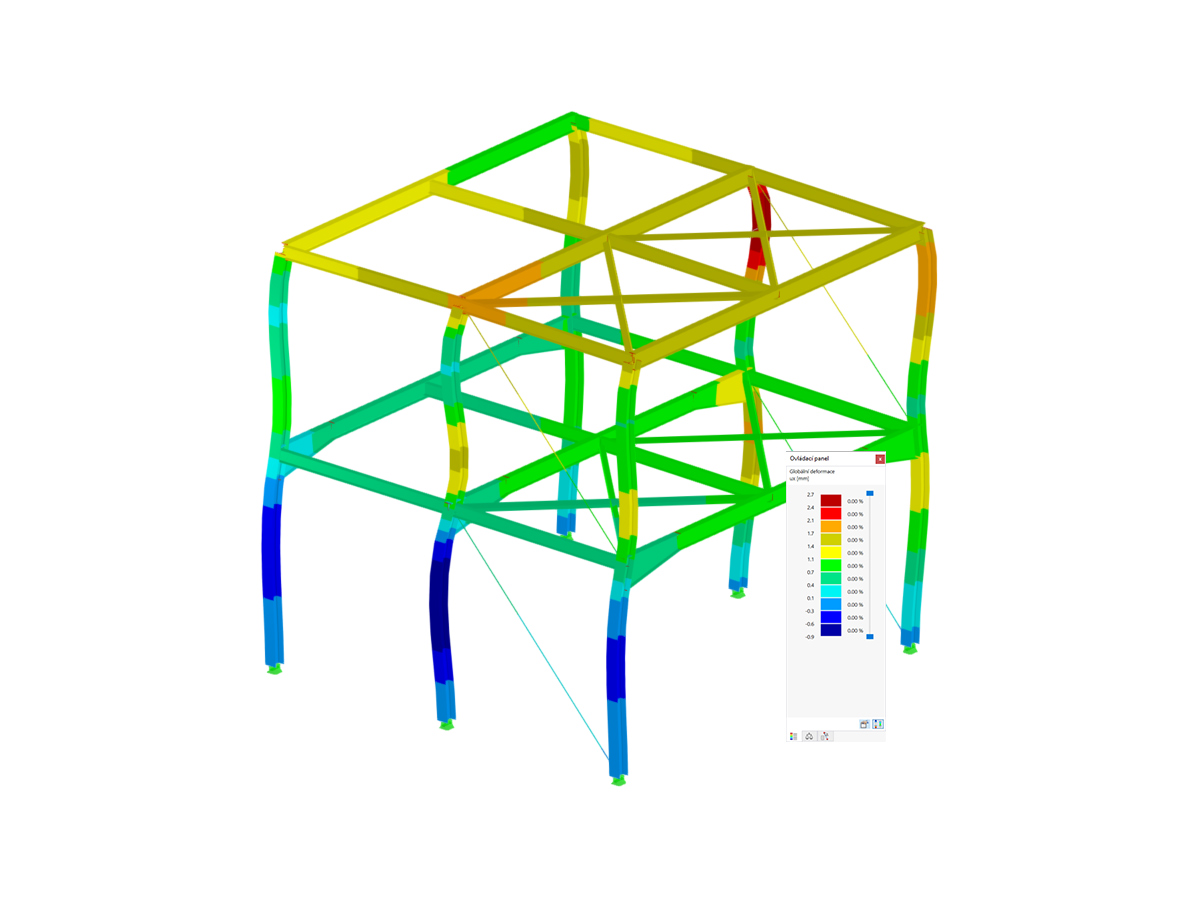
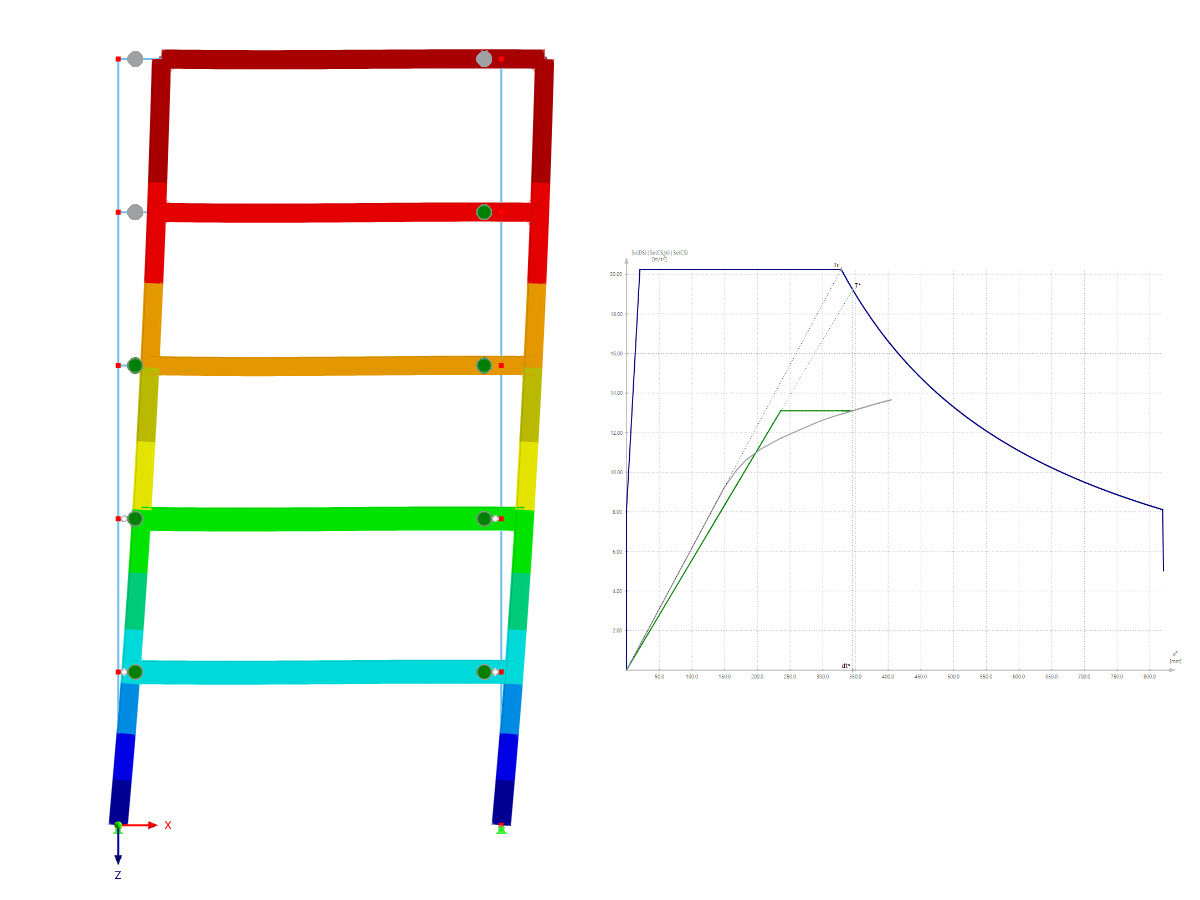
The results calculated manually can also be reproduced in RFEM (deformation) or in the steel design modules (stresses).

Result

The activation of the Bourdon effect in the global calculation parameters of RFEM is important for the deformation. If you want to consider not only the axial strain of pipes but also the expansion of pipe bends, you can use the RF-PIPING add-on module.

Literature

[1]	Franke, W.; Platzer, B.: Piping Basics - Planning - Assembly. Munich: Carl Hanser, 2014
[2]	Wikipedia: Barlow's formula

Author

Mr. Sühnel is responsible for the quality assurance of RSTAB; he also participates in product development and provides technical support for our customers.

Links

RFEM 5 Add-on Modules - Piping Systems

Downloads

RFEM Model File

2.38 MB

;