Uma configuração de análise estática ( SA ) especifica as regras de acordo com as quais os casos de carga e as combinações de carga são calculados. Estão predefinidos três tipos de análise padrão.
Geral
O separador Geral gere as configurações para os parâmetros de análise estrutural e de cálculo elementar.
Tipo de análise
Esta secção de diálogo controla a teoria de cálculo de acordo com a qual os casos de carga e as combinações de cargas são analisados. Na lista 'Tipo de análise', estão disponíveis três abordagens para seleção.
Geometricamente linear
Ao calcular de acordo com a análise geometricamente linear (Primeira ordem), o equilíbrio é analisado num sistema estrutural não deformado. É realizada uma análise linear porque as deformações dos componentes não são incluídas no cálculo.
Os casos de carga são calculados de acordo com a análise geometricamente linear.
Segunda ordem (P-Δ)
Na análise de segunda ordem "estrutural", o equilíbrio é determinado sobre um sistema estrutural deformado. As deformações são assumidas como sendo pequenas. As forças axiais no sistema têm impacto no aumento dos momentos fletores. Assim sendo, esta análise entra em vigor quando as forças axiais são significativamente maiores do que as forças de corte.
As combinações de carga são calculadas de forma não linear por defeito, de acordo com a análise de segunda ordem.
Deformações grandes
A análise de grandes deformações (de terceira ordem ou teoria das grandes deformações) considera forças longitudinais e transversais no cálculo. Após cada passo de iteração, é criada a matriz de rigidez de um sistema deformado. As cargas são movimentadas de forma diferenciada: Uma carga definida na direção global mantém a sua direção se os elementos finitos estiverem torcidos. Se a carga actua na direção de um eixo local da barra ou da superfície, muda a sua direção de acordo com a torção do elemento'.
Se o modelo inclui barras de cabo, o cálculo de acordo com a análise de grandes deformações já é predefinido.
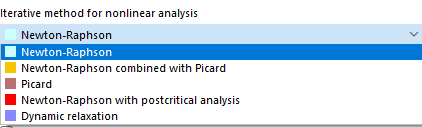
Método iterativo para análise não linear
Dependendo do tipo de análise, estão disponíveis vários métodos para resolver o sistema de equações algébrico não linear.
Newton-Raphson
A abordagem de acordo com Newton-Raphson está pré-definida para a análise das grandes deformações. O sistema de equações não linear é resolvido numericamente através de aproximações iterativas com tangentes. A matriz de rigidez tangencial é determinada como função do actual estado de deformação; é invertido em cada ciclo de iterações. Na maioria dos casos, é alcançada uma convergência rápida (quadrática).
Newton-Raphson combinado com Picard
A abordagem de acordo com Picard é aplicada primeiro. Após algumas iterações, é feita uma troca para o método Newton-Raphson. A ideia básica desta abordagem é utilizar o método de Picard, relativamente "insensível" para os primeiros passos da iteração, a fim de evitar mensagens de instabilidade. Esta aproximação inicial é seguida pelo método mais rápido de Newton-Raphson para encontrar o estado último de equilíbrio.
Picard
O método de Picard, também conhecido como método da secante, pode ser entendido como uma aproximação por diferenças finitas do método Newton-Raphson. A diferença entre a iteração atual e a original no passo de incremento de carga atual é considerada. Frequentemente, convergir é mais lento do que o método de cálculo de acordo com Newton-Raphson. No entanto, também se mostra menos sensível para problemas não lineares, o que torna o cálculo mais estável.
Newton-Raphson com análise pós-crítica
Este método é útil para resolver problemas pós-críticos onde existe um intervalo de instabilidade a ser ultrapassado. Se estiver disponível uma instabilidade e a matriz de rigidez não puder ser invertida, é utilizada a matriz de rigidez da última etapa de iteração estável. O cálculo com a matriz continua até ser alcançado novamente um intervalo de estabilidade.
Relaxação dinâmica
O método final é adequado para cálculos de acordo com a análise de grandes deformações e para resolver problemas pós-críticos. Nesta abordagem, é introduzido um parâmetro de tempo artificial. Tendo em consideração a inercia e o amortecimento, a ruptura pode ser gerida como um problema dinâmico. Esta abordagem utiliza o método da tempo-integração explicito; a matriz de rigidez não será invertida. Não é permitido que nenhuma parte do modelo tenha um peso específico de zero, quando calcula com o relaxamento dinâmico.
Este método inclui também o amortecimento de Rayleigh que pode ser definido através de constantes α e β de acordo com a seguinte equação com derivadas no tempo:
|
M |
Matriz de massa concentrada (diagonal) |
|
C |
Matriz de amortecimento diagonal C = α M + βdiag[K11 ( u ),K22 ( u ),...,Knn ( u )] |
|
K |
Matriz de rigidez |
|
f |
Vetor das forças externas |
|
u |
Vetor de deslocamento discretizado |
Controlos para análise não linear
O 'Número máximo de iterações' define quantas execuções de cálculos são realizadas para uma análise de acordo com ou análise de grandes deformações, bem como para objectos que actuam não linearmente. Quando o cálculo atinge o limite sem atingir um equilíbrio, aparece uma mensagem correspondente. Depois, pode decidir se pretende apresentar os resultados.
O 'número de incrementos de carga' é relevante para os cálculos de acordo com a segunda ordem ou análise de grandes deformações. Encontrar um equilibrio é muitas vezes dificultado quando são consideradas grandes deformações. As instabilidades podem ser evitadas aplicando um carregamento em várias etapas. Por exemplo, se especificar dois incrementos de carga, é aplicada metade da carga no primeiro passo. As iterações são realizadas até que seja encontrado um equilíbrio. Então, na segunda etapa, é aplicado o carregamento total ao sistema já deformado e são realizadas iterações novamente até que o equilíbrio seja alcançado.
Opções I
Nesta secção de diálogo, pode activar várias 'configurações especiais' para manipular os cálculos de acordo com ou análise de grandes deformações.
Modificar precisão padrão e configurações de tolerância
Quando você seleciona a caixa de seleção 'Modificar configurações de precisão e tolerância padrão', o separador Precisão e tolerância é adicionado à caixa de diálogo. Nela, pode ajustar os critérios de convergência.
Ignorar todas as não linearidades
Com a caixa de seleção 'Ignorar todas as não linearidades', pode desativar as propriedades não lineares dos elementos para o cálculo. Assim, as barras tracionadas, por exemplo, permanecem no modelo assim que ocorrem esforços de compressão. No entanto, as propriedades não lineares devem ser suprimidas apenas para fins de teste; por exemplo, para encontrar a causa de uma instabilidade. Critérios de rotura definidos incorretamente são por vezes responsáveis por interrupções de cálculo.
Opções II
Modificar o carregamento através do fator de multiplicação
Após seleccionar a caixa de seleção, pode definir um fator k pelo qual todas as cargas serão multiplicadas.
As normas mais antigas exigem a multiplicação das cargas globalmente por um determinado factor de forma a aumentar os efeitos de acordo com a análise de segunda ordem para as verificações de estabilidade. Por outro lado, o dimensionamento tem de ser realizado com as cargas caracteristicas. Ambos os requisitos podem ser satisfeitos introduzindo um fator maior que 1 e ativando a caixa de seleção 'Dividir resultados pelo fator de carga'.
Para análises de acordo com as normas em vigor, o carregamento não deve ser editado através de fatores. Em vez disso, os coeficientes de segurança parciais e de combinação devem ser considerados para a sobreposição nas situações de dimensionamento.
Considerar efeito favorável devido à tração em barras
As forças de tracção tem um efeito favorável sobre os sistemas estruturais pré-deformados. Assim, a deformação é reduzida e a estrutura é estabilizada. Geralmente, beneficiamos deste efeito em cálculos segundo a análise de segunda ordem e de grandes deformações; por exemplo, para pavilhões com contraventamentos ou estruturas gerais sujeitas a flexão. O alívio devido aos efeitos da força de tração para vigas reticuladas por baixo (vigas com tirantes ou cabos) pode resultar numa redução indesejada das deformações e dos esforços internos.
Verificação da estabilidade com base no grau de deformação
Se seleciona a caixa de seleção, o RFEM verifica a evolução das deformações ao longo das iterações durante o cálculo. Se os deslocamentos ou as rotações aumentarem muito e excederem um limite interno do programa, o cálculo é interrompido com uma mensagem de instabilidade.
Tentativa de cálculo da estrutura instável
Com esta caixa de seleção, pode tentar tornar um modelo instável calculável: No primeiro passo de cálculo, o RFEM aplica pequenas molas que estabilizam o modelo para a primeira iteração. Assim que um estado inicial estável é alcançado, as molas são removidas para as iterações subsequentes.
Deslocamentos devidos a carga de barra do tipo 'pressão interna da tubagem'
A caixa de seleção é relevante para a carga de barra denominada pressão interna da tubulação. O efeito de Bourdon descreve o esforço de um tubo curvado sob a influencia da pressão. Tanto as tensões perimetrais como as tensões axial causadas pela carga de pressão interna conduzem a uma deformação longitudinal do tubo, considerando a rigidez do material e a deformação transversal.
Consulte este artigo técnico que descreve um exemplo de cálculo da pressão interna de tubos.
Guardar os resultados de todos os incrementos de carga
Se o carregamento é aplicado de forma incremental (ver Controlos para análise não linear), pode utilizar esta caixa de seleção para forçar a saída de resultados intermédios a fim de verificar os resultados dos incrementos de carga individuais.
Solucionador não-simétrico direto
Um solucionador de equação direto não simétrico é usado para um modelo de material não linear (ver capítulo Comportamento de material não linear) com propriedades assimétricas para tração e compressão. A caixa de seleção permite-lhe utilizar este solucionador de equação também para outros modelos de material, tais como o modelo de material Isotrópico não linear elástico.
Equilíbrio para estrutura não deformada
A caixa de seleção permite-lhe analisar uma estrutura não deformada, ou seja, um sistema estrutural cujas deformações permanecem igual a zero. Esta opção de análise pode ser útil quando um sistema está sob tensão, por exemplo, devido a um caso de carga enquanto as deformações resultantes podem ser consideradas como tendo desaparecido.
Um campo de aplicação para o cálculo do equilíbrio para a estrutura não deformada é o estado de tensão primário da análise geotécnica. No âmbito de um caso ou combinação de carga, as tensões atuantes resultantes da pré-carga do solo devem ser determinadas. No entanto, as deformações de tal caso ou combinação de carga não são do interesse e, portanto, não podem ser utilizadas no futuro.
Configuração básica
O separador Configurações básicas gere as especificações básicas para o cálculo.
Relação da carga permanente
A caixa de seleção 'Determinar para combinações de cargas' oferece a possibilidade de determinar a relação de uma carga de ação permanente numa combinação de cargas. Selecione a combinação de carga na lista ou crie uma nova combinação de carga com o botão
![]() . Depois, na lista 'Comparar valor dos resultados', pode definir as relações que têm um efeito estático ou variável.
. Depois, na lista 'Comparar valor dos resultados', pode definir as relações que têm um efeito estático ou variável.
A relação da carga permanente pode ser considerada como estando em conformidade com as normas no dimensionamento.
Método para sistema de equação
Ambas as opções controlam os métodos utilizados para resolver o sistema de equação. Para prevenir uma interpretação errada: Mesmo quando o sistema de equação é resolvido diretamente, é realizado um cálculo iterativo se existem não linearidades ou se os cálculos são realizados de acordo com métodos de segunda ordem ou análise de grandes deformações. 'Directo' e 'Iterativo' referem-se à gestão de dados durante o cálculo.
Qual método de resolução de matrizes conduz mais rapidamente a resultados depende da complexidade do modelo e do tamanho da memória principal (RAM) disponível. Para sistemas de pequena e média dimensão, o método direto é mais eficiente.
Para sistemas muito grandes e complexos, o método iterativo leva a resultados mais rapidamente.
Teoria de flexão de placas
As superfícies podem ser calculadas de acordo com as teorias de flexão 'Mindlin' ou 'Kirchhoff'. No cálculo de acordo com Mindlin, as deformações da força de corte são incluídas; segundo Kirchhoff, não são considerados. A opção de cálculo Mindlin é, portanto, adequada para lajes e cascas relativamente espessas utilizadas em construções de sólidos, enquanto a opção Kirchhoff é recomendada para superfícies relativamente finas, tais como chapas de metal em estruturas em aço.
Configuração do método iterativo
As caixas de selecção nesta secção de diálogo são importantes para a análise 'Segunda ordem (P-Δ)'.
Relacionar esforços internos para a estrutura deformada
Os esforços e os momentos internos das barras são geralmente apresentados em relação à posição alterada do sistema de coordenadas de barra que surge no sistema deformado. Se pretende que a saída se refira ao sistema inicial não deformado, pode definir as forças internas e os momentos relevantes da barra desativando as caixas de seleção correspondentes.
Percentagem de iterações do Método Newton-Raphson em combinação com Picard
O método de acordo com Picard é baseado em rigidezes secantes, enquanto o método de Newton-Raphson se baseia em rigidezes tangentes. Quando a opção de cálculo Newton-Raphson combinado com Picard é selecionada, são utilizadas armaduras secantes nas primeiras iterações antes de serem aplicadas reforços tangentes para as restantes iterações. A relação das primeiras iterações com rigidezes secantes está relacionada com o número total de iterações.
Conversão de massa em carga
As cargas podem ser definidas não apenas como forças e momentos, mas também na forma de massas. No entanto, as massas não têm efeito na análise estrutural. Se pretende considerá-los, selecione a caixa de seleção 'Massa ativa'. Em seguida, introduz o 'Fator na direção' para descrever o efeito da massa. Assim, as massas são convertidas em forças antes de o cálculo iniciar e são incluídas na determinação das forças internas e dos momentos.
Utilize o botão
![]() para alternar entre a introdução do fator de massa e a introdução direta da aceleração. O nome dos campos de entrada é ajustado em conformidade.
para alternar entre a introdução do fator de massa e a introdução direta da aceleração. O nome dos campos de entrada é ajustado em conformidade.
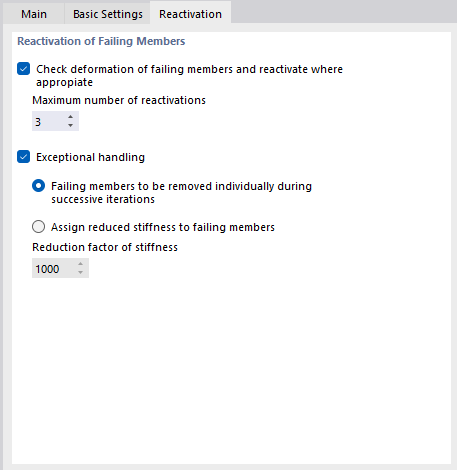
Reativação
O separador Reativação fica disponível assim que existe uma barra com propriedades não lineares no modelo. Neste separador, pode controlar como as barras em falha são tratadas na análise.
Barras com falha são frequentemente a causa de problemas de instabilidade, por exemplo, quando um modelo de barra é reforçado por barras tracionadas. Devido às contrações do pilar do pórtico devido à carga vertical, as barras tracionadas recebem pequenas forças de compressão na primeira etapa de cálculo. Estas serão eliminadas do sistema. Na segunda etapa, o modelo torna-se instável sem essas barras tracionadas. Com as opções da secção de diálogo 'Reativação de barras com falha', pode tentar realizar um cálculo sem mensagem de erro.
Verificar deformação das barras em rotura e, eventualmente, reativá-las
O RFEM analisa os deslocamentos nodais em cada iteração. Por exemplo, se as extremidades da barra de uma barra tracionada com rotura se afastam uma da outra, a barra é utilizada novamente na matriz de rigidez.
A reativação de barras pode ser problemática em alguns casos: Uma barra é removida após a primeira iteração, reativada após a segunda, removida novamente após a terceira iteração e assim por diante. O cálculo executaria esse loop até atingir o número máximo possível de iterações, sem convergir. O 'Número máximo de reativações' evita este efeito. Pode definir com que frequência um elemento de barra pode ser reinserido antes de ser finalmente removido da matriz de rigidez.
Manipulação excepcional
Se assinalar a caixa de seleção 'Manuseamento de exceções', pode selecionar entre dois métodos para lidar com barras com falha. Podem ser combinados com a reativação descrita acima.
- As barras em rotura são removidas individualmente durante as sucessivas iterações
Após a primeira iteração, o RFEM não remove, por exemplo, todas as barras tracionadas com uma força de compressão de uma só vez, mas apenas a barra tracionada com a maior força de compressão. Depois, na segunda iteração, apenas está em falta uma barra na matriz de rigidez. Posteriormente, a barra tracionada com a maior força de compressão é removida novamente. Desta forma, o sistema geralmente mostra um melhor comportamento de convergência devido aos efeitos de redistribuição.
Esta opção de cálculo requer mais tempo, porque o programa deve realizar um número maior de iterações. Além disso, é necessário garantir que é fornecido um número máximo de iterações suficiente na guia 'Main'.
- Atribuir rigidez reduzida a barras em rotura
As barras que entraram em ruptura não são removidas da matriz de rigidez. Em vez disso, o RFEM atribuí uma muito pequena rigidez às mesmas. Pode defini-lo no campo 'Fator de redução de rigidez': Um fator de 1000 significa que a rigidez da barra é reduzida para 1/1000.
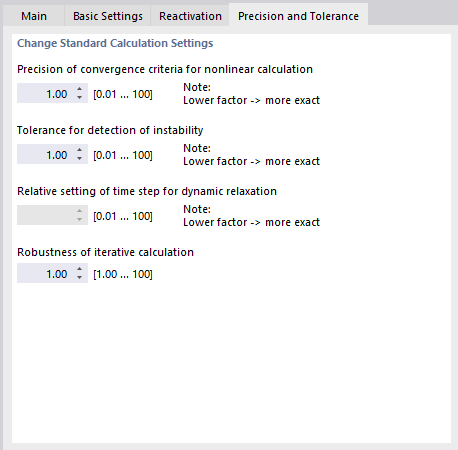
Precisão e tolerãncia
O separador Precisão e Tolerância permite-lhe influenciar os parâmetros de convergência e tolerância do cálculo. No entanto, as configurações padrão devem ser alteradas apenas em casos excepcionais.
Precisão do critério de convergência do cálculo não linear
Se efeitos não lineares estão em ação, ou se o ou é realizada uma grande análise de deformações, o cálculo pode ser influenciado por meio de critérios de convergência.
A alteração das forças axiais das duas últimas iterações é comparada barra a barra. Assim que a alteração atinge uma fracção específica da força axial máxima, o cálculo pára. No entanto, durante as iterações pode acontecer que as forças axiais oscilem entre dois valores. Pode evitar este efeito de pêndulo ajustando a "sensibilidade".
A precisão também afeta o critério de convergência para as alterações de deformação em cálculos realizados de acordo com a análise de grandes deformações, onde são consideradas não linearidades geométricas. O valor pré-definido é 1.00. O factor mínimo é de 0.01, o valor máximo é 100.0. Quanto menor o valor, mais próximo deve estar o termo de convergência do termo de comparação. A precisão dos resultados é aumentada em conformidade.
Tolerância para deteção de instabilidade
Existem diferentes abordagens para analisar o comportamento de estabilidade de um modelo. No entanto, nenhum deles é capaz de detectar matrizes de rigidez singulares com absoluta fiabilidade.
O RFEM utiliza dois procedimentos para determinar a instabilidade: Por um lado, os elementos na diagonal principal da matriz de rigidez são sempre comparados de forma absoluta com o mesmo número nas iterações. Por outro lado, cada elemento da diagonal principal é analisado em relação ao número adjacente. A tolerância pode ser ajustada no campo. Quanto menor o valor da tolerância, mais próximo o limite de instabilidade do modelo' está da localização exata da instabilidade. A precisão dos resultados é aumentada em conformidade.
Configuração relativa do incremento de tempo para o relaxamento dinâmico
O parâmetro de tempo controla o cálculo de acordo com o método de relaxação dinâmica. Quanto menor o valor, menor o passo de tempo através do qual todas as flutuações de resposta são registadas. A precisão dos resultados é aumentada em conformidade.
Robustez do cálculo iterativo
No caso de problemas de convergência com o método de Newton-Raphson, a robustez pode ser reforçada para evitar que a solução "pule". Ao reduzir o valor, o número de soluções possíveis é reduzido no caso de existir uma ramificação da solução horizontal não convergente e, assim, a possibilidade de obter um resultado válido dentro das iterações especificadas é reduzida também. Pode ser que seja necessário aumentar o número de iterações máximas.