Some of our recent Knowledge Base articles have focused on modeling members with circular hollow sections and their connections using RFEM 6 and the corresponding Steel Joints add-on. Two of these, namely KB 1887 and KB 1899, have shown you how to model some of these connections.
- KB 1887 | Modeling Simple End Plate Connection in RFEM 6
- KB 1899 | Modeling Stiffened Tubular Joints in Steel Joints Add-on
The first article showed how to model a simple end plate connection of two elements with circular hollow sections (that is, a connection with a ring flange), while the second one shows how to model the same connections, but stiffened with ribs. In Image 1, both connections are shown, the former under a) and the latter under b).
However, when modeling and designing such joints, we must consider some important aspects that could affect their performance. One of them is the prying of the fasteners due to tensile forces. This force is caused by the bending of the end plate and can lead to increased bolt stress and plastic deformations. The above-mentioned joints are examples of steel joints that are susceptible to this prying effect, as they are joints with an end plate where the bolts are outside the connected cross-section.
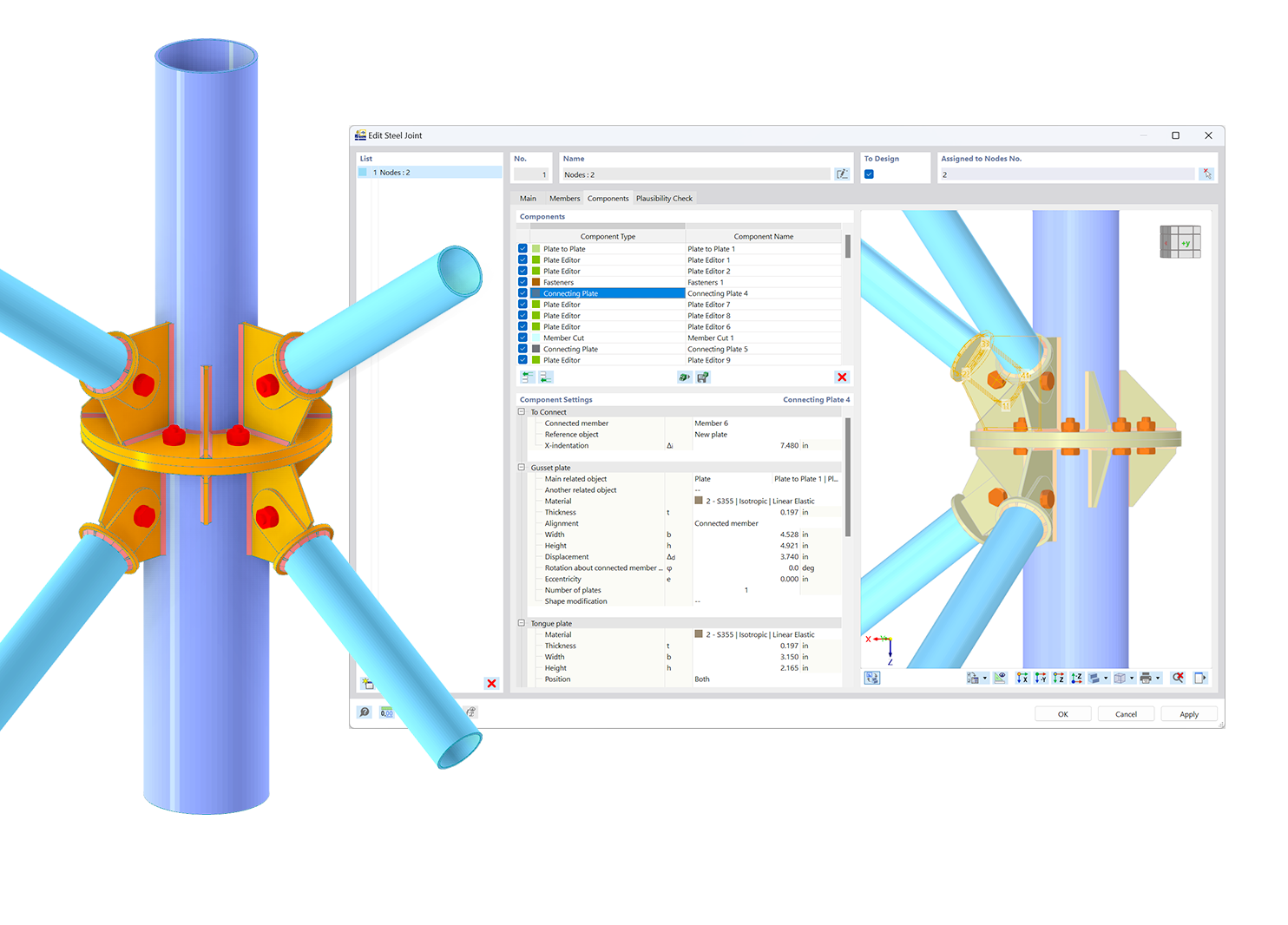
Dlubal's Steel Joints add-on can accurately capture the prying effect and include it in the results of the numerical model (that is, forces on bolts, plastic deformation of the connected plates, overall connection deformation). Therefore, it would be interesting to investigate and compare this effect in the flange joints mentioned above, as will be done in this article.
But first let us look at how this issue is addressed in the design codes; more specifically, in Eurocode 3 [1]. According to EC.3, Section 6) of 6.2.4.1, in cases where prying forces may occur, the design tensile resistance of a T-stub flange should be taken as the smallest value for the three possible failure modes:
- Mode 1: Complete yielding of the flange
- Mode 2: Bolt failure with yielding of the flange
- Mode 3: Bolt failure
Each of these modes is detailed in Table 6.2 of EC 3 [1]. A brief description of the concept is given in Image 2, where:
| Q | Prying force, that is, the contact force which may occur between the free edge and the bolt row, applied as the resultant of the surface pressure in the contact gap at the boundary point of the stub flange |
| FT,Rd | Design tension resistance of a T-stub flange |
| dw | Diameter of the washer, or the width across points of the bolt head or nut, as relevant |
| n, m | Distances as indicated in the figure |
Before we proceed, we also need to determine what factors influence the prying effect. These would be the distance of the bolt from the cross-section, the stiffness and geometry of the end plate, the bolt deformation, and the welding solution.
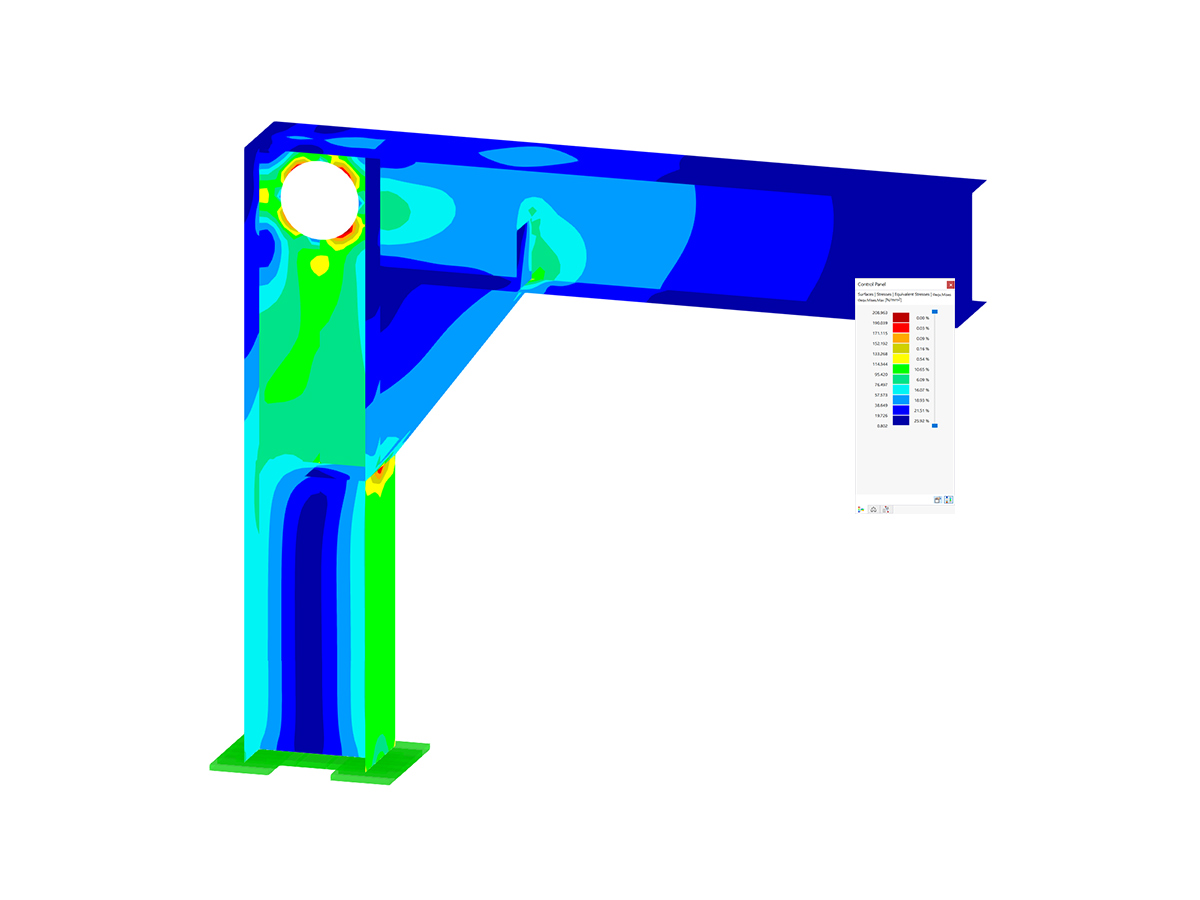
With this background, we can now consider the prying effect in the two variants of CHS profile flange connections mentioned at the beginning of this text. To broaden the consideration of the topic, we add another variant to them: namely, we will also consider the prying effect in a full end plate without an opening, as shown in Image 3.
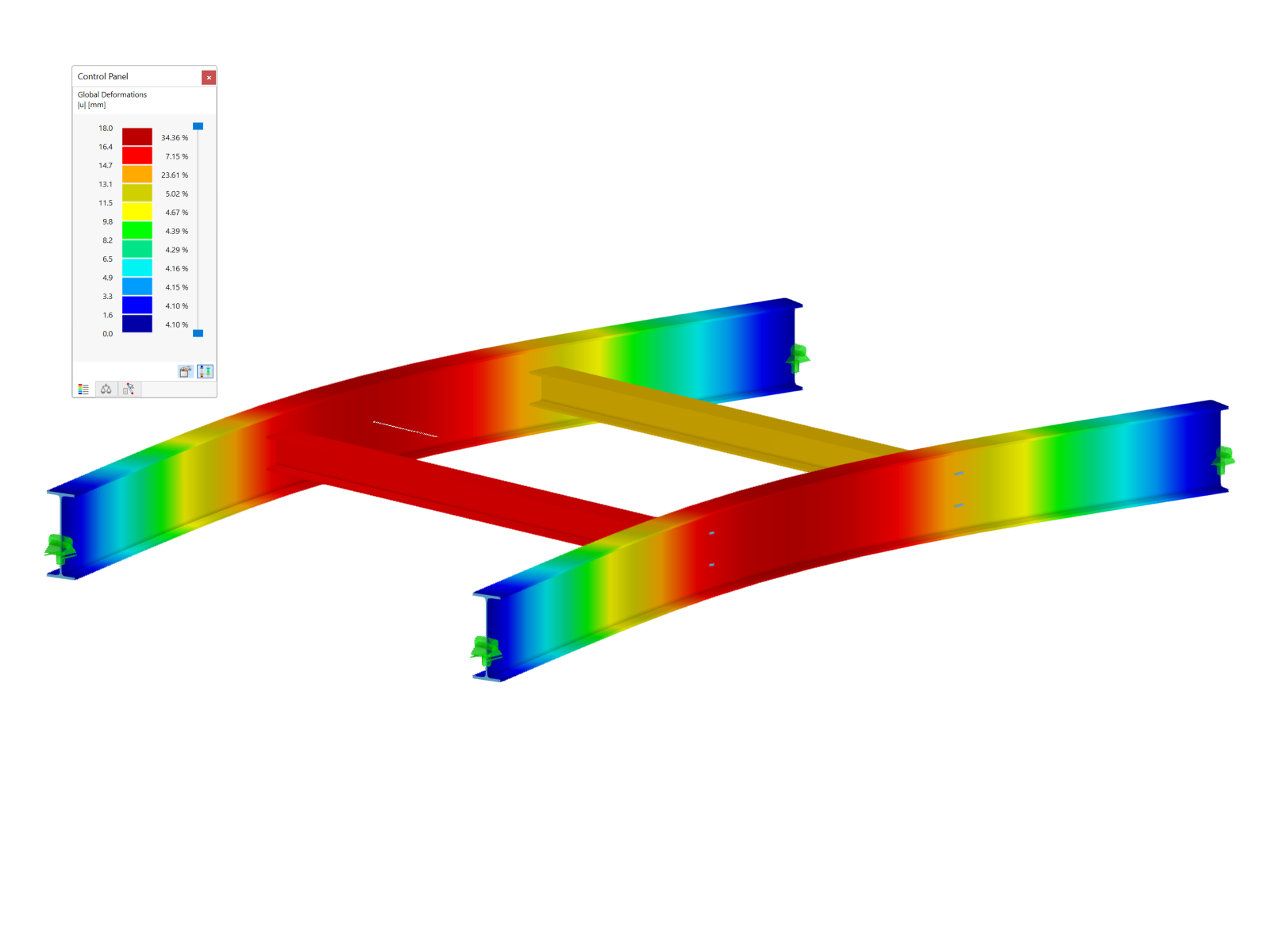
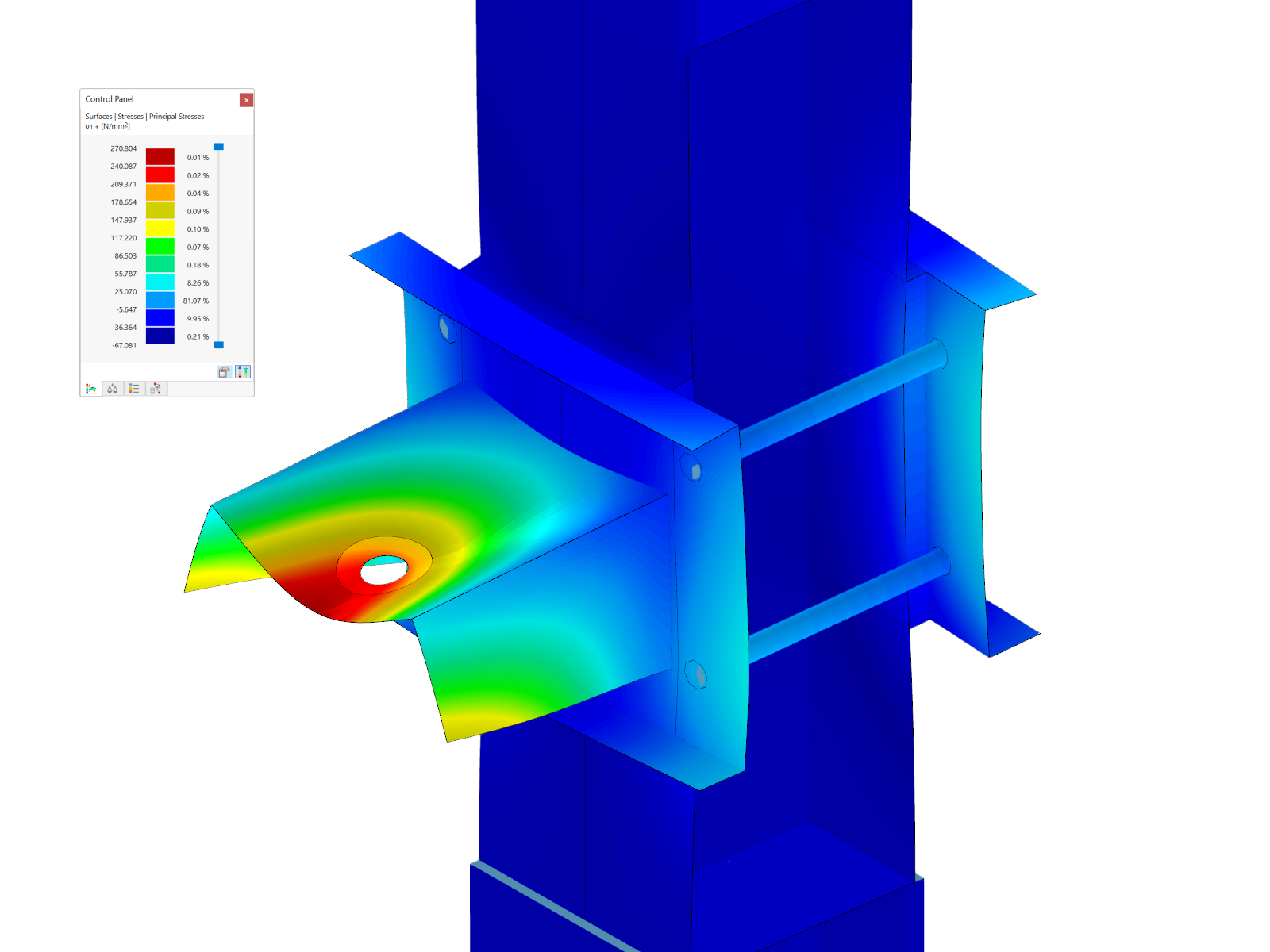
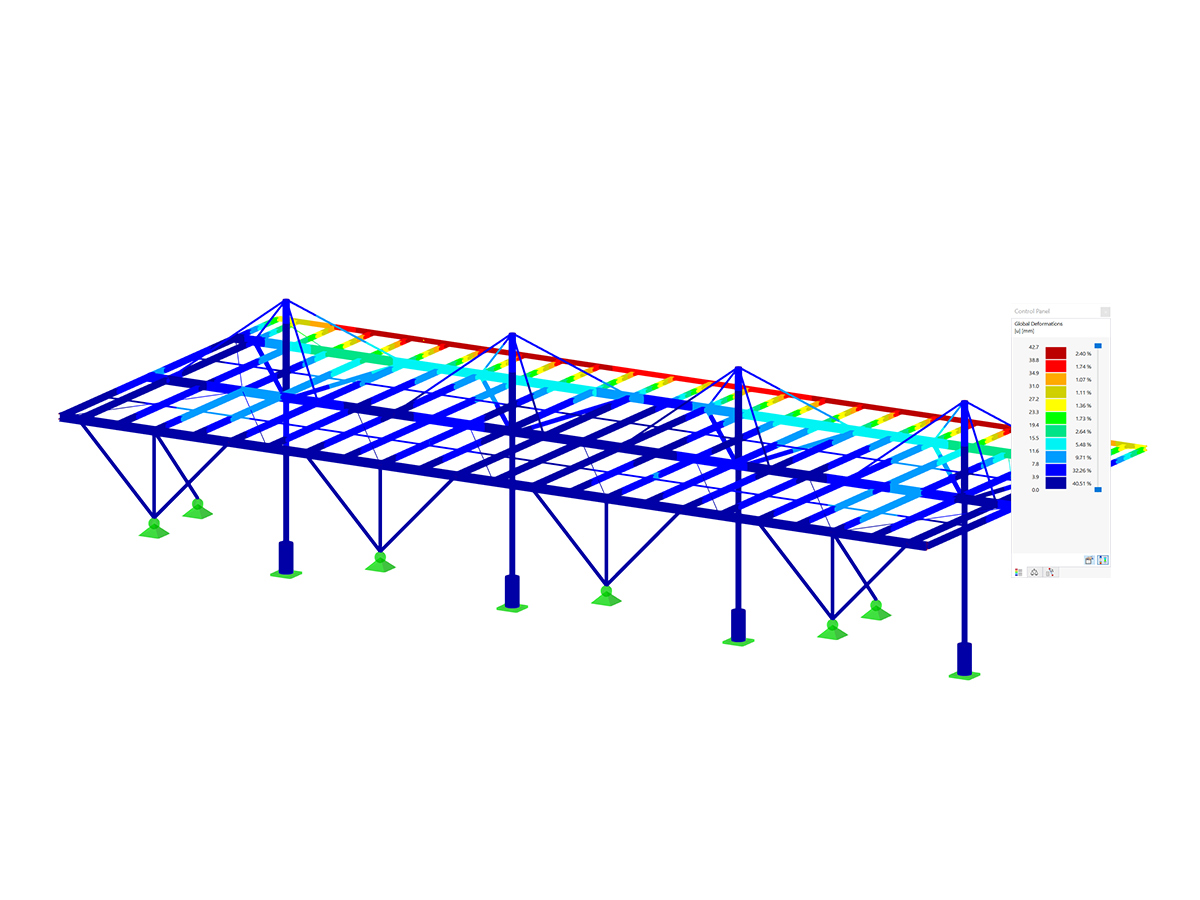
As mentioned before, Dlubal’s Steel Joints add-on can realistically capture the prying effect and include it in the results of the numerical model. Therefore, we can create these connections (Images 4, 5, and 6) in RFEM 6 and subject the model to a tensile force of 300 kN, as shown in Image 7.
Then, we can run the calculation and obtain the forces in the bolts as shown in Image 8.
To compare the behavior of the three variants, prying effect coefficients are used, which are expressed as the ratio of the total force in the bolts to the applied force. Once the former has been determined as shown in Image 8, the prying effect for each of the variants can be calculated easily, as shown in Table 1.
| Variant | Applied Tensile Force [kN] | Total Bold Force [kN] | kRFEM,1 |
|---|---|---|---|
| 1. Ring Flange | 300 | 515.3 | 1.72 |
| 2. Full End Plate | 300 | 423.8 | 1.41 |
| 3. Stiffened Ring Flange | 300 | 300 | 1 |
The prying coefficients determined in Table 1 clearly show that prying is the highest in the joint when ring flanges are used. We can also see that an end plate without an opening provides some relief, while stiffeners reliably relieve the bolts of prying forces and reduce the plastic deformation of the end plate. Since we have already determined which parameters affect prying, we can conclude that to reduce/eliminate this effect, a thick end plate and larger bolt diameters would be required for the first variant when ring flanges are used.
On the other hand, the end plate with the stiffened ring flange (that is, Variant 3) would remain thinner, but we must consider that stiffeners would have to be welded on, which increases the cost of the joint. If the prying effect is small, it may not be worth welding stiffeners. However, if this effect is significant, there may be no other option than to reinforce the joint. Since both scenarios have an impact on production costs, we must be able to choose the optimal solution to minimize production costs while maintaining the good performance of the joint.
Conclusion
The optimal design of joints plays an important role in the design of steel structures. Therefore, it is crucial to understand and carefully consider the aspects relevant to the design of the connections in these structures. Prying is one of the harmful phenomena that cannot be overlooked when designing bolted joints. In most cases, in joint types that are prone to prying, such as those discussed in this article, parameters such as plate thickness, number and diameter of bolts, an so on, are determined by this effect. This is because these parameters affect the prying and must be chosen in such a way that, on one hand, they reduce this effect, but on the other hand, they also contribute to the optimal design of the joint (for example, in terms of production cost).




















































.png?mw=350&hash=dc38fc2ddc3754a07164885d9707318b00be194d)








-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)






.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)