3046x

001548

Amy Heilig, PE

2018-12-05

2018 NDS Updates for Cross-Laminated Timber Design

The American Wood Council (AWC) has released the 2018 Edition of the National Design Specification (NDS) for Wood Construction. This is the second edition of the NDS to contain a chapter dedicated to cross-laminated timber (CLT) design. Therefore, a couple of revisions were included in the 2018 NDS when compared to the previous 2015 Edition.

Revision 1: Format Conversion Factor, K_F (LRFD only) - Section 10.3.10

The format conversion factor, K_F, is specified in Table 10.3.1 [1]. This value is taken into consideration when calculating the rolling shear strength, F_s, per LRFD only. The factor simply adjusts the reference ASD design value to the LRFD reference resistance. Previously, this factor was set to 2.88 in the 2015 NDS. In the 2018 standard, the value was updated to 2.00.

The RF-LAMINATE module has been updated to account for the new K_F factor of 2.00 when designing as per ANSI/AWC NDS-2018 and LRFD.

Format Conversion Factor, KF, when Designing per 2018 NDS and LRFD in RF-LAMINATE

Revision 2: Apparent Bending Stiffness for Deflection Calculations - Section 10.4.1

The 2018 NDS states in Section 10.4.1 [1] that the deflection of a CLT panel must include the effects of bending as well as shear deformation. The standard goes on to suggest reducing the effective bending stiffness, EI_eff, to account for shear deformation as a function of the panel loading and support conditions, geometry, span, and effective shear stiffness. The stiffness adjusted for shear deformation is referred to as the apparent bending stiffness, (EI)_app, and can be calculated as per equation 10.4-1 [1]. This equation has been slightly modified from the 2015 standard.

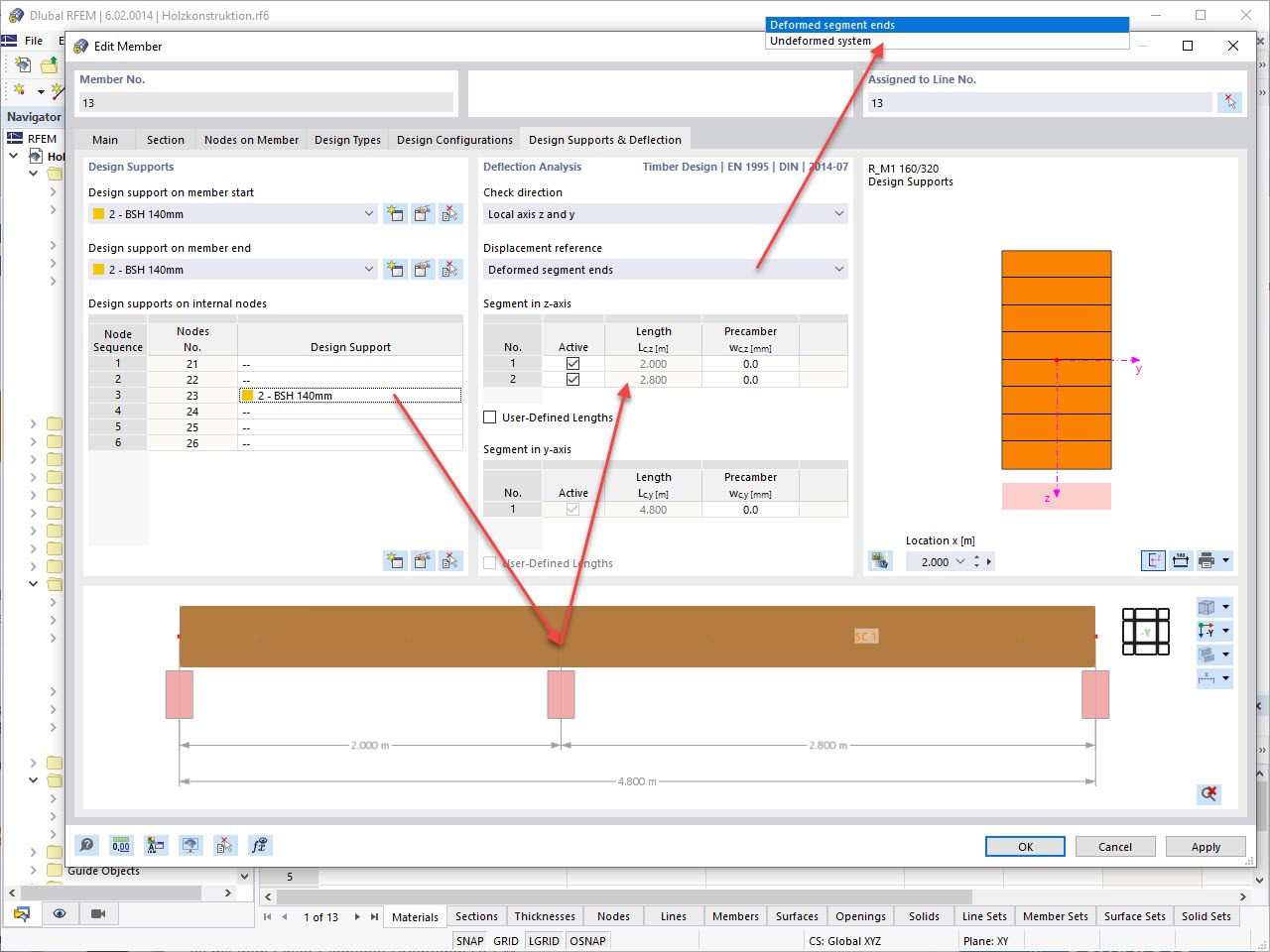
In RFEM and RF-LAMINATE, it is not possible to consider (EI)_app since the Shear Deformation Adjustment Factor, K_s, must be determined for each panel from Table 10.4.1.1 [1]. K_s depends on both the loading conditions (that is, uniformly distributed, line load at mid-span, line load at quarter points, and so on), as well as the end fixity (that is, fixed, pinned, cantilever, and so on). These variables do not necessarily fall into the defined categories defined in Table 10.4.1.1, but rather may include several different loading conditions or end fixity. Therefore, RF-LAMINATE takes on a different and more exact approach to account for the effects of shear deformation.

RF-LAMINATE applies the Laminate Theory to calculate the effective shear stiffness for a CLT panel. The overall stiffness matrix for each panel is comprised of multiple stiffness entries including bending and torsion, shear, membrane, and eccentricity with the D₄₄ and D₅₅ entries specifically related to shear stiffness.

Shear Stiffness Entries D44 and D55 in the CLT Panel Overall Stiffness Matrix:

\begin{array}{l} D = [\begin{matrix} D_{11} & D_{12} & D_{13} & 0 & 0 & D_{16} & D_{17} & D_{18} \\ D_{22} & D_{23} & 0 & 0 & sym . & D_{27} & D_{28} \\ D_{33} & 0 & 0 & sym . & sym . & D_{38} \\ D_{44} & D_{45} & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym . & D_{66} & D_{67} & D_{68} \\ D_{77} & D_{78} \\ D_{88} \end{matrix}] \\ Bending and Torsion : D_{11} D_{12} D_{13} D_{22} D_{23} D_{33} \\ Shear : D_{44} D_{45} D_{55} \\ Membrane : D_{66} D_{67} D_{68} D_{77} D_{78} D_{88} \\ Eccentricity : D_{16} D_{17} D_{18} D_{27} D_{28} D_{38} \end{array}

Formula 1

General technical regulations [2] suggest that in order to calculate the effective shear stiffness, the shear stiffness must be reduced by applying a shear correction coefficient, κ, in the panel's x and y directions. Effective Shear Stiffness = κGA
with
κ = shear correction coefficient
G = shear modulus
A = section area

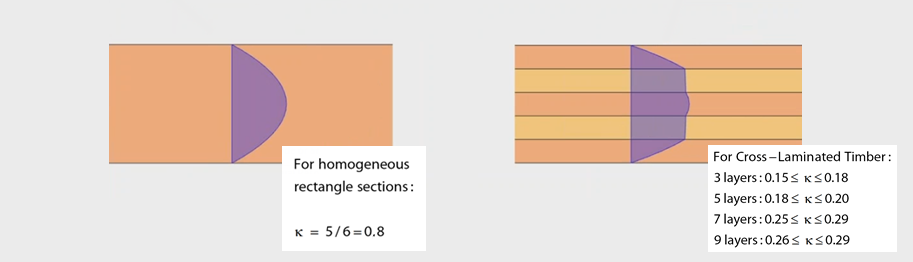
For a typical homogeneous material, the shear stress distribution when viewing the cross-section of the element represents a parabolic shape. A κ value of 5/6 or 0.8 is typically used for this homogeneous material. However, when looking at the shear stress distribution of a CLT panel, the shape is no longer parabolic and the material is not considered homogeneous, but rather isotropic. Therefore, the 0.8 factor cannot be used. There are several approximations for the shear correction coefficient for CLT panels depending on the number of cross-layers.

Estimates of Shear Stress Distribution and Shear Correction Factor

In RF-LAMINATE, the shear correction coefficient is indirectly considered when calculating the D₄₄ and D₅₅ stiffness matrix entries according to the Grashof integral formula [3].

D_{44, calc}^{''} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{1}{G_{xz}^{''} (z)} (\frac{\int_{z}^{t / 2} E_{x}^{''} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{''} (\bar{z}) (\bar{z} - z_{0, x})^{2} d \bar{z}}) d z}, z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{x}^{''} (\bar{z}) \bar{z} d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{''} (\bar{z}) d \bar{z}}

Formula 2

D_{55, calc}^{''} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{1}{G_{yz}^{''} (z)} (\frac{\int_{z}^{t / 2} E_{y}^{''} (\bar{z}) (\bar{z} - z_{0, y}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{''} (\bar{z}) (\bar{z} - z_{0, y})^{2} d \bar{z}}) d z}, z_{0, y} = \frac{\int_{- t / 2}^{t / 2} E_{y}^{''} (\bar{z}) \bar{z} d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{''} (\bar{z}) d \bar{z}}

Formula 3

The values of stiffnesses D₄₄, D₅₅ are given by the following equations where l is the mean length of the lines surrounding the surface as a "box".

D_{44}^{''} = \max (D_{44, calc}^{''}, \frac{48}{5 l^{2}} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{x, i}^{''} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{x, i}^{''} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Formula 4

D_{55}^{''} = \max (D_{55, calc}^{''}, \frac{48}{5 l^{2}} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{y, i}^{''} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{y, i}^{''} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Formula 5

The D₄₄ and D₅₅ entries automatically calculated in RF-LAMINATE will now consider the required shear stiffness reductions. The same stiffness matrix will further be used in RFEM to calculate the panel deflections. Therefore, the requirements of the 2018 NDS considering both bending and shear deformation for deflection calculations as per Section 10.4.1 are met by taking a more exact approach with the Laminate Theory, as opposed to approximating the effects of shear deformation by reducing the effective bending stiffness.

Author

Amy Heilig is the CEO of the USA Subsidiary Office in Philadelphia, PA. She is responsible for sales, technical support, and continued program development for the North American market.

Links

Structural Analysis and Design Software for Timber Structures

References

American Wood Council. (2018). National Design Specification (NDS) for Wood Construction 2018 Edition. Leesburg: AWC.
Schickhofer, G.; Bogensperger, T.; Moosbrugger, T.: BSPhandbuch - Holz-Massivbauweise in Brettsperrholz - Nachweise auf Basis des neuen europäischen Normenkonzepts, 2. Auflage. Graz: Verlag der Technischen Universität Graz, 2010
Handbuch RF-LAMINATE. Tiefenbach: Dlubal Software, September 2016.

;

2018 NDS Updates for Cross-Laminated Timber Design

Revision 1: Format Conversion Factor, KF (LRFD only) - Section 10.3.10

Revision 2: Apparent Bending Stiffness for Deflection Calculations - Section 10.4.1

Revision 1: Format Conversion Factor, K_F (LRFD only) - Section 10.3.10