2018年NDS更新交叉层压木结构设计

新规定1： 格式转换系数K_F （仅LRFD）-10.3.10节

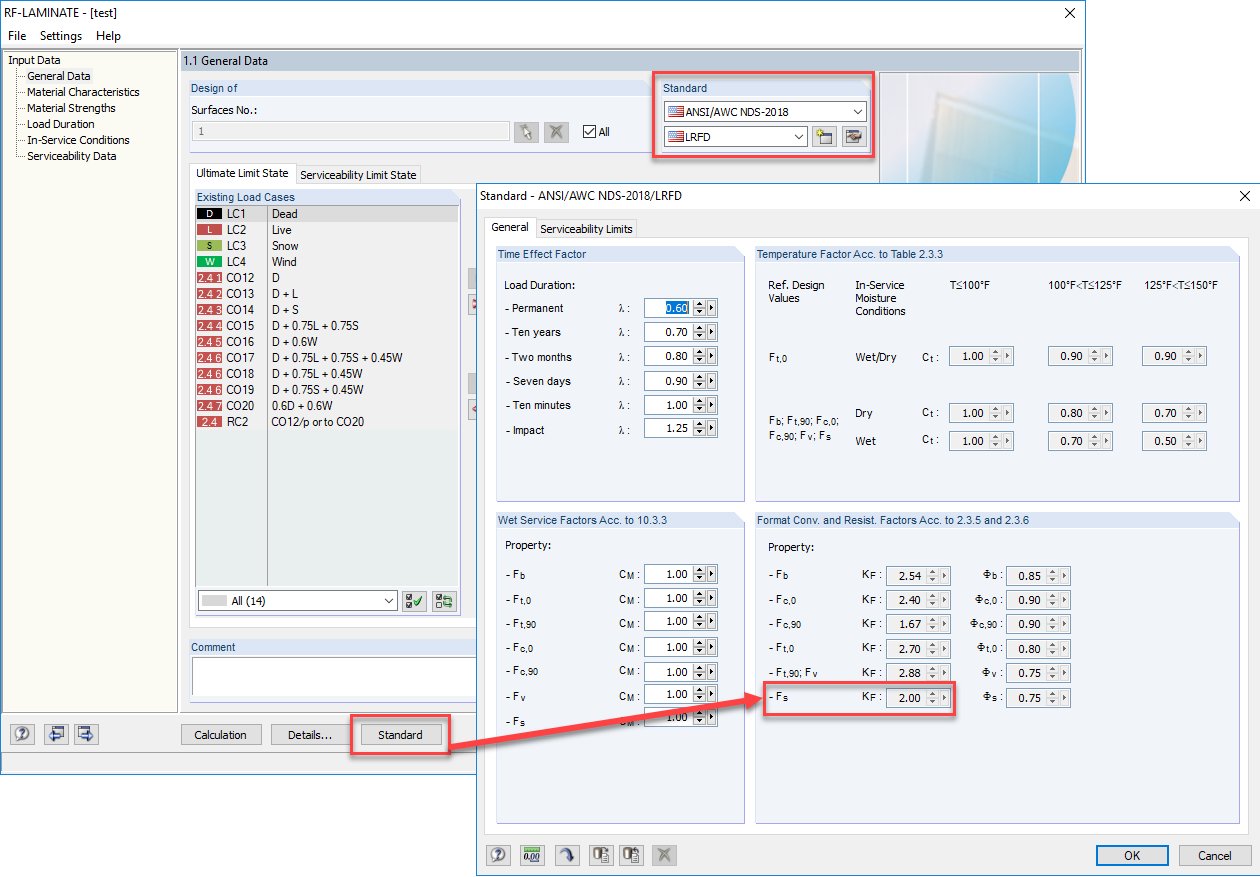
格式转换系数K_F在表10.3.1 [1]中有更详细的说明。 如果仅使用LRFD计算滚动剪力F_s，则考虑该值。 该系数将ASD参考设计值调整为LRFD参考电阻。 以前在2015年NDS中该系数设置为2.88。 在2018年版本中，该值已更正为2.00。

The RF-LAMINATE module has been updated to account for the new K_F factor of 2.00 when designing as per ANSI/AWC NDS-2018 and LRFD.

Formatkonvertierungsfaktor KF bei Bemessung nach NDS 2018 und LRFD in RF-LAMINATE

新规定2： 挠度计算中出现的抗弯刚度-第10.4.1节

The 2018 NDS states in Section 10.4.1 [1] that the deflection of a CLT panel must include the effects of bending as well as shear deformation. 该标准还建议减小有效抗弯刚度EI_eff ，以考虑剪力变形随板荷载以及支座条件，几何形状，跨度和有效抗剪刚度的变化。 The stiffness adjusted for shear deformation is referred to as the apparent bending stiffness, (EI)_app, and can be calculated as per equation 10.4-1 [1]. 该公式与2015年标准有所不同。

在RFEM和RF-LAMINATE中不能使用（EI）_app，因为每个板的剪力变形K_s的调整系数必须按照表10.4.1.1 [1]确定。 K_s depends on both the loading conditions (that is, uniformly distributed, line load at mid-span, line load at quarter points, and so on), as well as the end fixity (that is, fixed, pinned, cantilever, and so on). These variables do not necessarily fall into the defined categories defined in Table 10.4.1.1, but rather may include several different loading conditions or end fixity. 因此，RF-LAMINATE提供了一种不同且更精确的方法来考虑剪力变形的影响。

RF-LAMINATE使用层板理论计算胶合板的有效抗剪刚度。 每个板的整个刚度矩阵由多个刚度输入组成，包括弯曲和扭转，剪力，膜和偏心，以及D₄₄和D₅₅输入，特别是与剪力有关。

胶合木面板的整个刚度矩阵中的抗剪刚度输入D44和D55：

General technical regulations [2] suggest that in order to calculate the effective shear stiffness, the shear stiffness must be reduced by applying a shear correction coefficient, κ, in the panel's x and y directions. 有效抗剪刚度=κGA
这里
κ=剪力修正系数
G =剪切模量
A =截面积

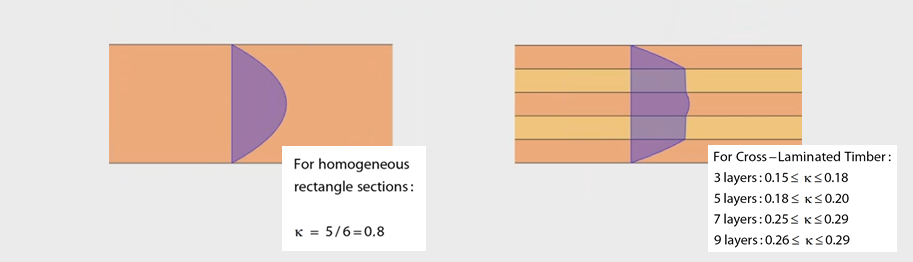
对于典型的均质材料，当考虑单元的截面时，剪应力分布为抛物线形。 对于这种均质材料，通常使用κ值为5/6或0.8。 However, when looking at the shear stress distribution of a CLT panel, the shape is no longer parabolic and the material is not considered homogeneous, but rather isotropic. 因此不能使用系数0.8。 胶合木胶合板的剪力校正系数有一些估算，这取决于横向层的数量。

Schätzungen Schubspannungsverlauf und Schubkorrekturfaktor

在RF-LAMINATE中，当按照Grashof积分公式[3]计算D₄₄和D₅₅刚度矩阵项时，间接考虑剪力系数。

刚度D₄₄ ，D₅₅的值由下面的公式给出，其中l是围绕面的线的平均长度，即“盒子”。

在RF-LAMINATE中自动计算的输入项D₄₄和D₅₅现在考虑所需的抗剪刚度折减。 在RFEM中使用相同的刚度矩阵来计算板的挠度。 Therefore, the requirements of the 2018 NDS considering both bending and shear deformation for deflection calculations as per Section 10.4.1 are met by taking a more exact approach with the Laminate Theory, as opposed to approximating the effects of shear deformation by reducing the effective bending stiffness.