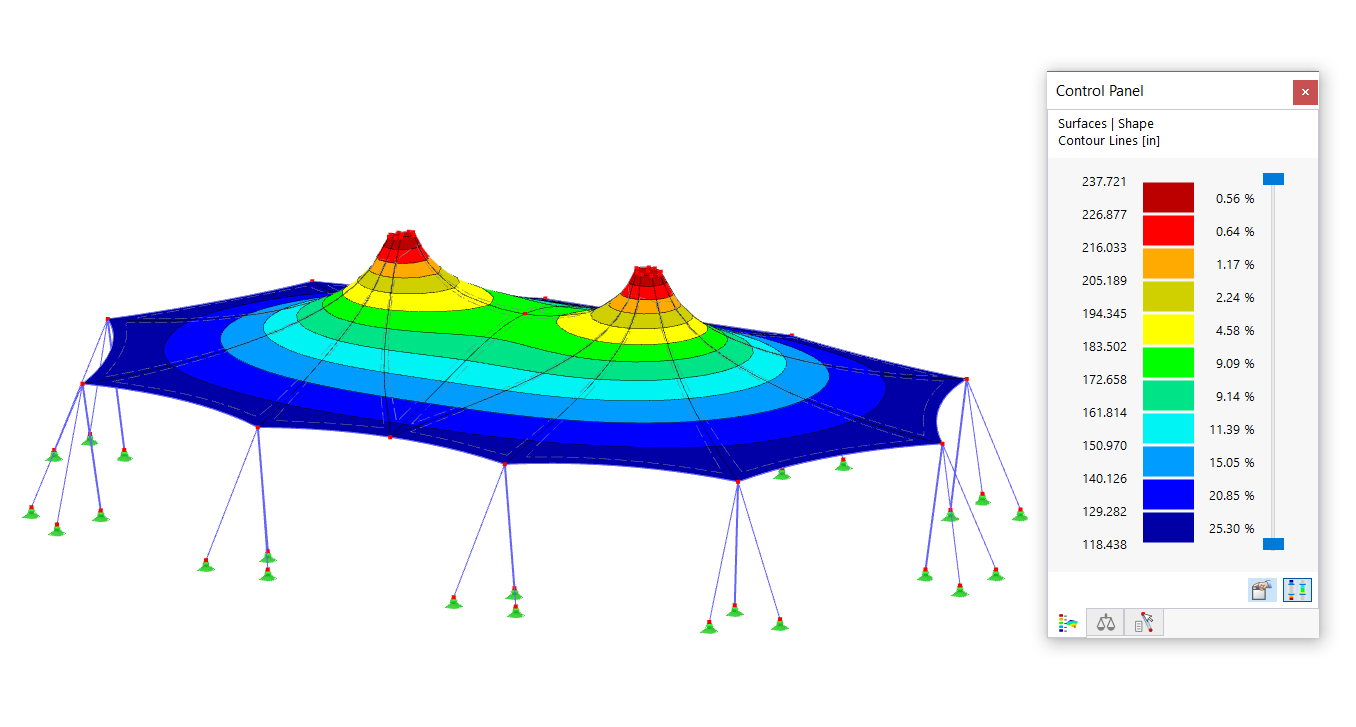
In RFEM 6 and RSTAB 9, you can perform modal analysis using the Modal Analysis add-on as one of the add-ons available for dynamic analysis. The features of this add-on were discussed in a previous Knowledge Base article titled:
Features of Modal Analysis Add-on for RFEM 6
. This article will show you a practical example of how to use this add-on for determining the natural vibration values of a reinforced concrete multi-story structure.
Practical Example
You can activate the Modal Analysis add-on in the model's Base Data. In the Standards II tab of the Base Data window, you can select the standard used for the dynamic analysis, so that the input dialog boxes of the dynamic analysis are automatically adjusted to the selected standard (Image 1).
In contrast to RFEM 5, where you are asked to provide the input data for the modal analysis in the associated add-on module, the Modal Analysis add-on in RFEM 6 is fully integrated into the program itself. Thus, the user interface is extended by new entries in the navigator, tables, and dialog boxes after activating the add-on and selecting the design standard.
This way, you can initialize the input of data for the modal analysis directly in the Load Cases & Combinations window. The first step is to create a load case with modal analysis as an analysis type (Image 2) and import masses directly from load cases or load combinations of interest.
You can create a design situation based on a selected design codes and use it for modal analysis, as in the load combination selected in Image 2, as discussed in the previous Knowledge Base article:
Features of Modal Analysis Add-on for RFEM 6
. In this example, the combinations are created according to the EN 1990 standard and the German national annex (DIN | 2012-08) shown in Image 3.
Hence, you can create a design situation with a seismic mass combination type based on which the program will automatically generate a load combination with the preset combination coefficients for the selected standard. This load combination, in fact, contains the masses to be used for the modal analysis (Image 4). When importing the masses, load components in the global Z-direction are considered by default (Image 5).
The modal analysis settings can be defined further in the Modal Analysis Settings window, where you can select the method for determining the number of mode shapes (Image 6). In this example, the number of the smallest mode shapes to be calculated is manually set as 12. Another option is to set the maximum natural frequency so that the mode shapes are automatically determined until the set natural frequency has been reached.
The method for solving the eigenvalue problem is also to be selected from the three available methods in RFEM 6: Lanczos, roots of characteristic polynomial, and subspace iteration. In RSTAB 9, on the other hand, two methods are available: subspace iteration and shifted inverse iteration. Although all of them are suitable for determining the exact eigenvalues, the choice is conditioned by the size of the support system to be considered.
In this example, the Lanczos method is employed to determine the n-lowest eigenmodes and the corresponding eigenvalues of the structure. Next, the masses are defined as acting in the global X and Y directions. You can also consider masses rotating around the global axes X, Y, and Z, but considering the structure in this example, this is not necessary.
Once the modal analysis settings have been defined, you can start the calculation and obtain the results in both graphical and tabular form. Hence, in addition to the display of masses (discussed in more detail in the Knowledge Base article titled:
Features of Modal Analysis Add-on for RFEM 6
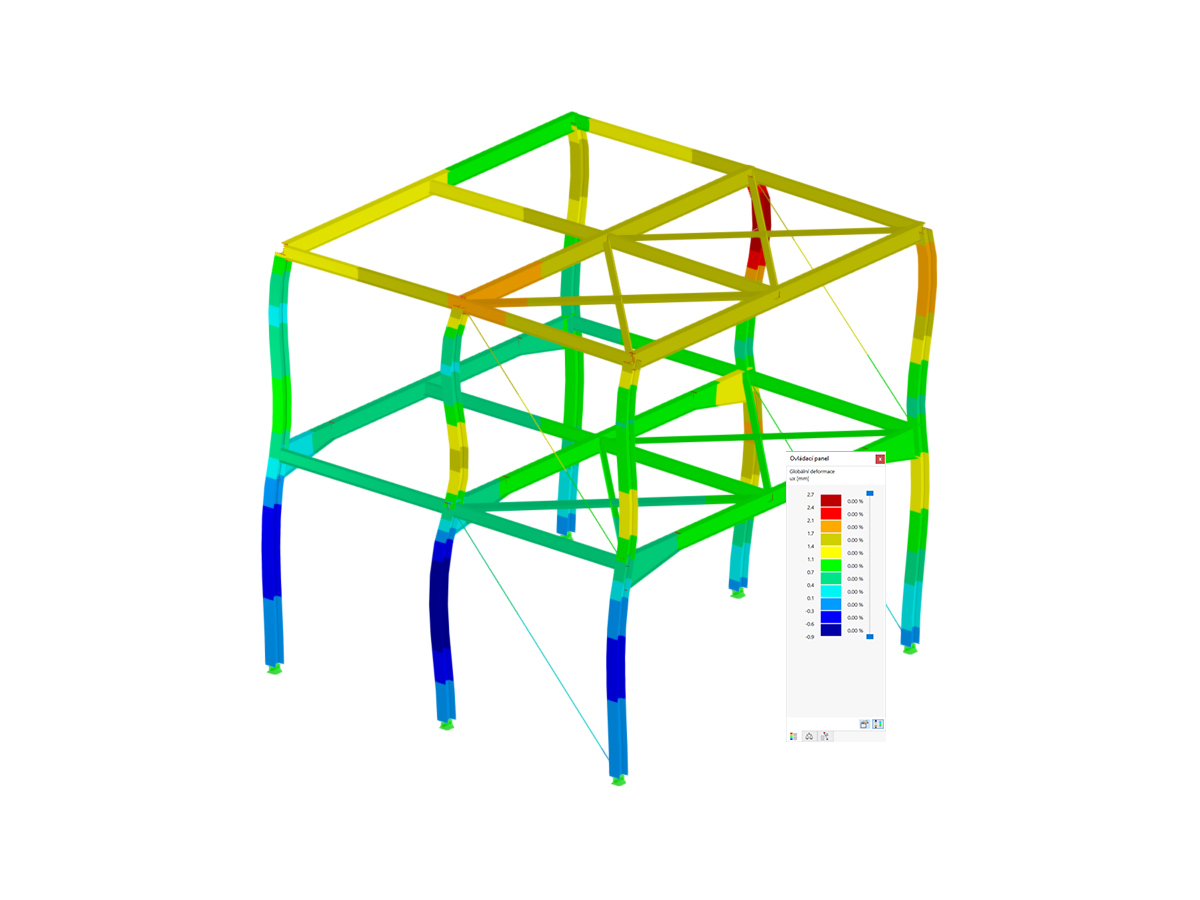
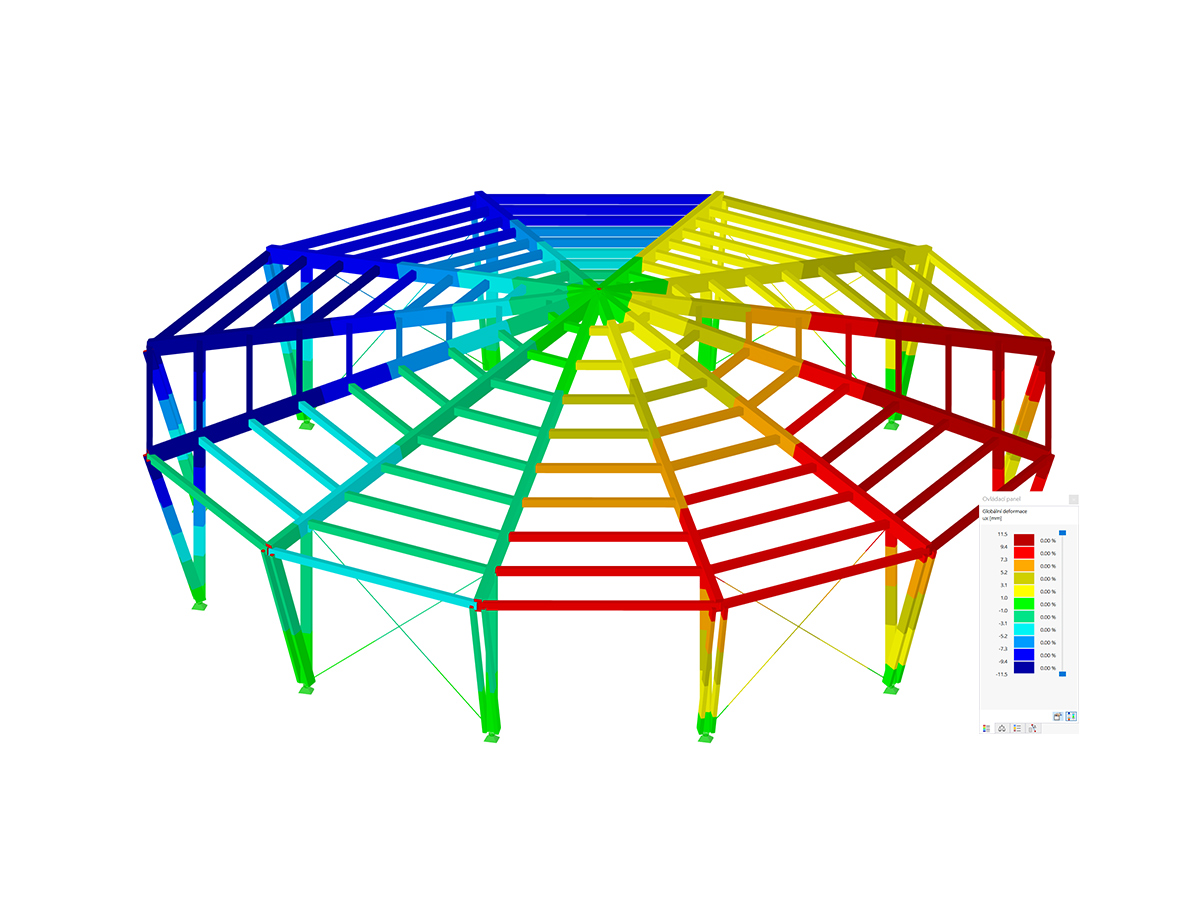
), the Results navigator allows you to see all the mode shapes of the structures, as shown in Image 7.
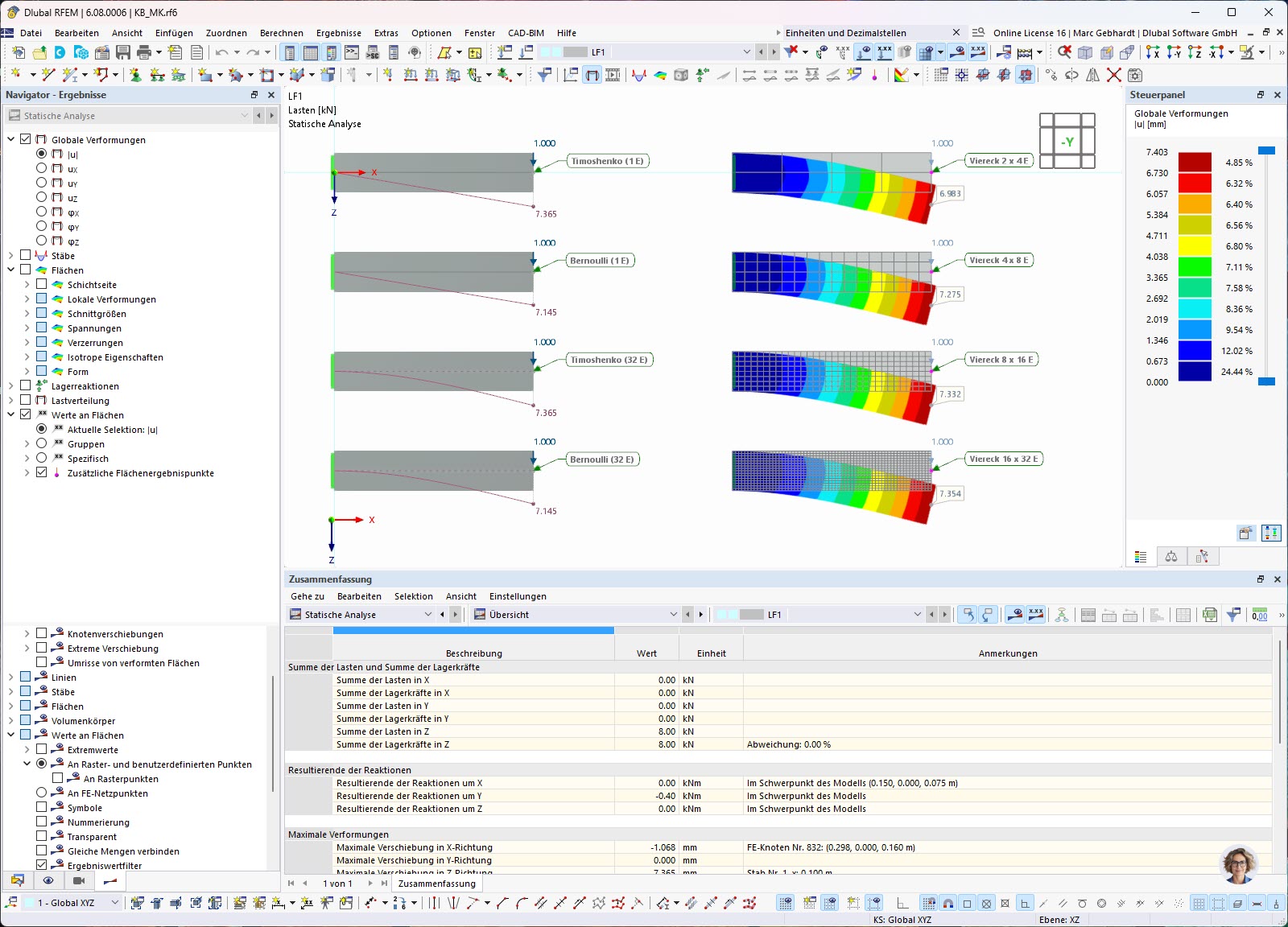
The natural frequencies of the corresponding eigenmodes can be found in the navigator, but also in the Results table as shown in Image 7. As a matter of fact, the Natural Frequency tab of the Modal Analysis results table provides you with an overview of the eigenvalues, angular frequencies, natural frequencies, and natural periods of your undamped system.
The values are obtained by calculating the equation of motion of a multiple degree of freedom system, without damping with the set eigenvalue solver. Based on the eigenvalues λ [1/s2], the angular frequencies ω [rad/s] are derived, given that they are related though the relation λi = ωi2. Next, the natural frequency f [Hz] is obtained by considering that f = ω/2π. Finally, the natural period T [s] can be calculated as the reciprocal of the frequency (that is, T = 1/f).
In the Results tables for the modal analysis, you can also display the effective modal masses (which describe how much mass is activated in each direction by each eigenmode of the system), the corresponding modal mass factors, and the participation factors. For instance, if you are interested in performing a response spectra analysis afterwards, you can check whether the effective modal mass factors of a specific shape have to be considered for the response spectrum calculation according to the requirements of the certain standard. This is shown in Image 8.
Final Remarks
You can use the Modal Analysis add-on to determine the natural vibration values of structures, such as natural frequencies, mode shapes, modal masses, and effective modal mass factors in RFEM 6. The features of the add-on are discussed in more detail in a previous Knowledge Base article titled: Features of Modal Analysis Add-on for RFEM 6 .
This article, on the other hand, shows you a summary of how to perform a modal analysis in RFEM 6. Thus, all you must do is to create a load case of a modal analysis type, import masses directly from load cases or/and load combinations of interest, and define the analysis settings.
Once you do the calculation, the results in terms of natural frequency values, effective modal masses, participation factors, and masses in mesh points are available to you. This outcome can be used for design purposes and for further dynamic analysis in the program (for example, loading by a response spectrum).

































































.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)