In addition to the normal snow load, which is applied to the roof below, another load from slipping and drifted snow has to be considered. These two additional loads are distributed in a triangular shape over the drift length Is.
Additional impact loads due to the snow sliding off the higher roof may also have to be taken into account.
| γ | Weight density of snow = 2 kN/m³ |
| h | Height of split-level slab |
| sk | Characteristic value of the snow load on the ground in kN/m² |
| sad | Design value for accidental snow loads on the soil of the location concerned |
| Cesl | Coefficient for accidental snow loads |
| ls | Drift length = |
If the length of the lower roof b2 is shorter than the drift Is, the load ordinates must be cut off at the edge of the roof.
μ1 = 0.8 (assuming that the lower roof is flat)
μ2 = μs + µw
μ s = shape coefficient for snow sliding off
α ≤ 15°: μs = 0
α > 15°: μs results from an additional load that is distributed in a triangular shape over the length ls. As an additional load, 50% of the resulting snow load is applied to the adjacent roof side of the higher roof.
| μ | Shape coefficient of the higher roof = 0.8 (regardless of the roof inclination) |
| μw | Snow load shape coefficient due to wind = |
In addition, the sum of the shape coefficients μw + μs can be limited by the National Annex (Germany) as follows.
General case (permanent, temporary situation):
0.8 ≤ μw + μs ≤ 2.4
Canopies open at the side and accessible for artificial removal (b2 ≤ 3 m):
0.8 ≤ μw + μs ≤ 2
For snow regions according to DIN EN 1991-1-3: 2010-12 and DIN EN 1991-1-3/A1: 2015-12, Figure C.2, the upper limit applies to snow loads of sk ≥ 3.0 kN/m²:
1.2 ≤ μw + μs ≤ (6.45/sk0.9 )
Exceptional actions (North German Plain) in general:
0.8 ≤ μw + μs ≤ 2.4
In the case of an accidental action, µw does not have to be set larger than
µw = ( γ ⋅ h ) / s
where
sad = Cesl ⋅ sk
When arranging snow fences or other obstructions, μs can be omitted.
Example
- b1 = 10 m
- b2 = 5 m
- h = 3 m
- Roof inclination of the higher roof = 30°
- A = 100 m
- Snow load zone 2
- μ1 = 0.8
- sk = 0.25 + 1.91 ⋅ ((A + 140)/760)² ≥ 0.85 → 0.85 kN/m²
Uniformly distributed snow load on the lower roof:
μ1 ⋅ sk = 0.8 ⋅ 0.85 kN/m² = 0.68 kN/m²
Drift length:
Shape coefficient for snow sliding off:
μs = 0.67
Snow load shape coefficient due to wind:
Limitation of shape coefficients (general case):
0.8 ≤ μw + μs ≤ 2.4
μ2 = μw + μs = 2.5 + 0.67 = 3.17 → 2.4
μ2 ⋅ sk = 2.4 ⋅ 0.85 kN/m² = 2.04 kN/m²
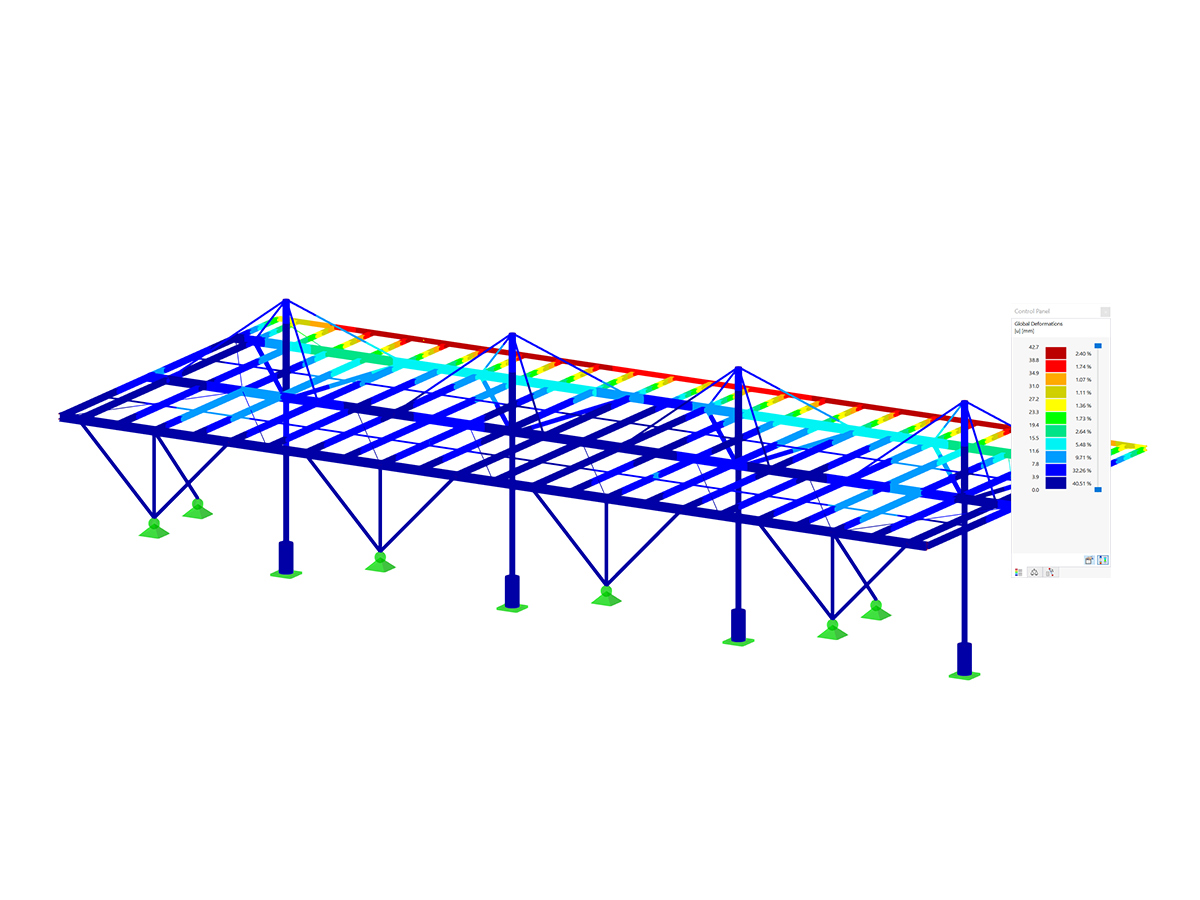
In RFEM and RSTAB, you can apply the load from snow drift and sliding snow as a linearly variable surface load. If you use frame structures, you can apply the load with the load generator.
