Essential Form-Finding Process
Practically, the materials used for membrane structures are subjected to tension resistance only. All loads are transferred solely by tension. In order to ensure a sufficient resistance and shape consistency of membrane structures, it is necessary to provide the adequate prestress.
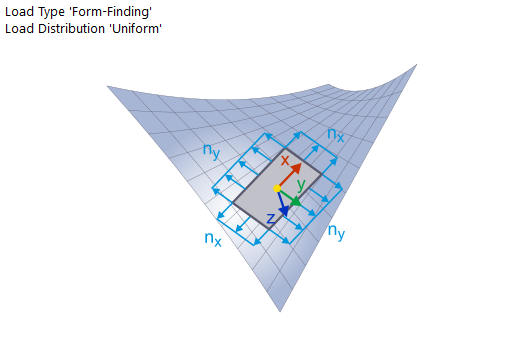
Due to the zero stiffness of the materials, it is not possible to separate the shape layout from the prestress design, because the shape is defined by the prestress. Each spatial system of force equilibrium (that is, the equilibrium of prestressing forces) clearly determines the spatial shape of a membrane structure. By defining boundary conditions and prestress forces in the equilibrium state, the actual shape of the membrane structure is specified. Searching for the shape of a membrane structure as a function of the defined prestress is called form-finding.
There are two different approaches to the form-finding process:
- Definition of boundary conditions and prestress ➝ A corresponding equilibrium shape is sought.
- Definition of boundary conditions and a shape (deformation) of the membrane ➝ An equilibrium prestress is sought.
Both methods are valid and have their advantages. However, the interaction between shape and loading prestress must never be neglected. By using the second approach, you can affect the final shape more easily, while the first one facilitates the design of the final prestress.
As the loading prestress is governing for the bearing resistance and endurance of the structures, the "Form-Finding" add-on provides this method for form-finding as well.
Key Features of Form-Finding Process
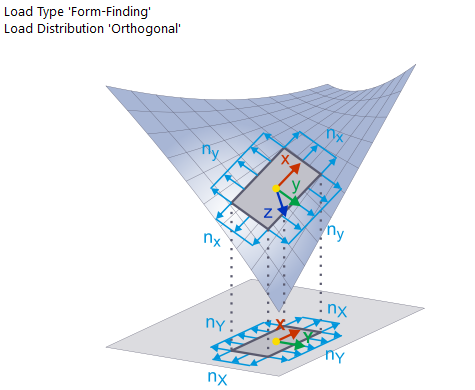
There is a direct correlation between the prestress and the shape of membrane structures. The properties of the fabrics used are irrelevant. The form-finding process is independent of the material.
In addition to boundary conditions and prestresses, the shape of a membrane structure can also be affected by loads. Thus, for pneumatically prestressed membranes, the program seeks the equilibrium shape for the defined prestress and interior pressure.
The load due to the self-weight may also affect the form-finding process. It is possible to search for a shape that corresponds to the specified prestress, the self-weight, and the interior pressure, if applicable. However, the self-weight applied in the form-finding process hardly influences the final shape and prestress, since the self-weight of the fabric is low.
Application Method for Form-Finding
The shape of a membrane structure is clearly defined by the boundary conditions and equilibrium prestress, or by the equilibrium between the prestress and load (internal pressure, self-weight), if necessary. However, it is difficult to define the equilibrium prestress, that is, the spatial equilibrium of forces.
When designing a membrane structure, isotropic prestress is usually the only equilibrium prestress that you can define in advance. However, such prestress does not always prove to be suitable – both in terms of the actual shape and the subsequent nonlinear analysis. Moreover, it may occur that a shape that conforms to the isotropic prestress is physically not possible due to specific boundary conditions.
Hence, it is necessary to specify an orthotropic prestress in the form-finding process. A constant orthotropic prestress in the equilibrium state is only possible if the Gaussian curve of the respective surface is equal to zero (for example, in the case of plane or cylindrical surfaces). Double-curved membrane structures are not characterized by this property. It would be necessary to provide the membrane with a general spatial orthotropic
prestress. However, this is unrealistic and would require a tool that is able to find, in addition to the equilibrium shape, the equilibrium prestress by specifying the prestresses in two directions (warp and weft directions).
In "Form-Finding", two calculation methods are implemented that you can use to find equilibrium shapes and prestresses – the projection method and the standard method. Both methods are based on the well-known form-finding method Updated Reference Strategy (URS) published by K. U. BLETZINGER and E. RAMM in 1999 [1].
In the case of conical shapes, the membrane structure does not constrict as much with the projection method (1) as with the standard method (2):
Although the shape of both canvases is the same, the standard method (2) approximates the applied prestress better than the projection method (1):
Projection Method
As already mentioned, it is virtually impossible to define a general equilibrium prestress in space. Nor in a plane where constant orthotropic prestress (orthogonally oriented prestress) can also be present, in addition to the isotropic prestress. Furthermore, when defining a loading prestress in the radial direction, it is also possible to determine the prestresses in the tangential direction for all adjacent points on the basis of a certain equilibrium condition.
These conditions are used by the projection method that is based on the "projection" of the prestress defined in the global XY plane into the actual position of the membrane structure. If the membrane inclination against the global XY plane is equal to zero, the prestress in the membrane corresponds to the specified values. If the membrane inclination against the global XY plane is not equal to zero, the prestress increases in the fall line direction, while the prestress decreases in the contour line direction. If the membrane inclination against the global XY plane is almost perpendicular, the prestress in the fall line direction increases significantly while the prestress in the contour line direction is close to zero.
This method allows the prestress equilibrium to be preserved in the directions of the global axes X and Y. In the form-finding process, the program then seeks the layout of the membrane structure in space that provides for an equilibrium prestress also in the direction of the global axis Z. The projection method, where the equilibrium prestress is determined in the projection, leads to the definition of the equilibrium prestress in space, and thus to finding a clear spatial shape of the membrane structure.
For finding the equilibrium state, the Updated Reference Strategy [1] method is used. Therefore, the form-finding process represents a nonlinear problem.
Standard Method
The standard method is very different from the projection method as the defined prestress is not modified (stabilized). When determining the equilibrium shape, the standard method applies the two specified values that were previously defined for the prestress in the warp and weft direction.
Usually, a prestress that is physically out of equilibrium (except isotropic prestress) is specified. Therefore, when applying the orthotropic prestress, for example, of 2.0 kN in the warp direction and of 1.0 kN in the weft direction, it is not to be expected that a shape of the membrane structure is achieved with a prestress that exactly meets these requirements. Since the requirement for a constant orthotropic prestress usually reflects no adequate solution, the shape would not converge to the equilibrium position when using this prestress repeatedly in the iteration process. For this reason, the selected prestress in the membrane structure is applied only in a certain number of iterations. Then, the stabilization is applied.
The standard method uses the fact that, when defining a presstress out of the equilibrium for a membrane structure, the deformations perpendicular to the membrane plane are more frequent than the deformations within the membrane plane. Once the specified number of iterations to use the prescribed prestress has been reached, the structure is stabilized. The resulting prestress comes usually very close to the specified values. The standard method is also based on the Updated Reference Strategy method of form-finding [1].
Form-Finding for Combined Structures (Membranes, Cables)
While the shape of membranes in "Form-Finding" is determined by means of the defined prestress values, it is possible for cables to define, in addition to prestresses, geometrical requirements, such as the final rise or length.
Membranes are often parts of a structure that contains a lot of bending-resistant elements (beams, plates, shells, and so on). During the form-finding process, an equilibrium shape of the entire structure is sought. The prestress in the membrane and cables has an active effect on the rigid elements of the structure, which have to counteract this prestress.
If you do not want to consider the influence of rigid elements in the form-finding process,
you can define temporary states by using structure modifications, or construction stages (the Construction Stages Analysis add-on). This allows you to fix the elements for the form-finding process and to show stiffnesses for these states.
Although the shape of both canvases is similar, the stiffness of the columns (2) has an influence on the shape and the distribution of internal forces, compared to the simplification with nodal supports (1):

























.png?mw=512&hash=4a84cbc5b1eacf1afb4217e8e43c5cb50ed8d827)