Un paramètre pour l’analyse statique (SA) définit les règles selon lesquelles les cas de charge et les combinaisons de charges sont calculés. Trois types d’analyse standard sont prédéfinis.
Base
L’onglet Base gère les paramètres pour l’analyse statique et les paramètres de calcul élémentaires.
Type d’analyse
Cette section contrôle selon quelle théorie de calcul les cas de charge et les combinaisons de charges sont analysés. Dans la liste « Type d’analyse », trois approches sont disponibles.
Analyse statique linéaire
Lors du calcul selon l’analyse statique linéaire, l’équilibre est étudié sur le système non déformé. Il s’agit d’une analyse linéaire, car les déformations des composants ne sont pas prises en compte dans le calcul.
Les cas de charge sont calculés par défaut de manière linéaire selon l’analyse statique linéaire.
Analyse du second ordre (P-Δ)
Dans l’analyse du second ordre « statique des structures », l’équilibre est déterminé sur le système déformé. Les déformations sont considérées comme petites. Les efforts normaux dans le système entraînent une augmentation des moments fléchissants. L’analyse du second ordre est ainsi utilisée lorsque les efforts normaux sont nettement supérieurs aux efforts tranchants.
Les combinaisons de charges sont calculées par défaut de manière non linéaire selon l’analyse du second ordre.
Analyse des grandes déformations
L’analyse des grandes déformations (« théorie des grandes déformations ») prend en compte les forces longitudinales et transversales lors du calcul. Après chaque pas d’itération, la matrice de rigidité du système déformé est formée. Les charges sont traitées de manière différenciée : une charge définie dans une direction globale conserve sa direction lorsque les éléments finis subissent une rotation. Si la charge agit dans la direction d’un axe local de barre ou de surface, elle change de direction en fonction de la rotation de l’élément.
Si le modèle contient des tirants ou des surfaces membranaires, le calcul selon l’analyse des grandes déformations est prédéfini.
Méthode itérative pour l’analyse non linéaire
Selon le type d’analyse, différentes méthodes sont disponibles pour résoudre le système d’équations algébriques non linéaires.
Newton-Raphson
Pour l’analyse des grandes déformations, la méthode de Newton-Raphson est prédéfinie. Le système d’équations non linéaires y est résolu numériquement par des approximations itératives avec des tangentes. La matrice de rigidité tangentielle est déterminée en fonction de l’état de déformation actuel ; elle est inversée à chaque cycle d’itération. Dans la plupart des cas, cette méthode permet d’atteindre une convergence rapide (quadratique).
Newton-Raphson combiné avec Picard
Cette méthode utilise d’abord la méthode de Picard. Après quelques itérations, un passage à la méthode de Newton-Raphson a lieu. L’idée principale de cette approche est d’utiliser la méthode de Picard relativement « insensible » pour les premiers pas d’itération afin d’éviter les messages d’instabilité. Avec l’approximation initiale, la méthode rapide de Newton-Raphson est ensuite utilisée pour trouver l’état d’équilibre final.
Picard
La méthode de Picard – également appelée méthode de la sécante – peut être comprise comme une approximation par différences finies de la méthode de Newton-Raphson. La différence entre le cycle d’itération actuel et le cycle d’itération initial dans le pas de charge actuel est considérée. Cette méthode converge généralement plus lentement que la méthode de calcul de Newton-Raphson. Elle s’avère cependant plus insensible aux problèmes non linéaires, ce qui rend le calcul plus stable.
Newton-Raphson avec problème de claquage
Cette méthode est adaptée à la résolution de problèmes de claquage où une zone d’instabilité doit être surmontée. Lorsqu’une instabilité est présente et que la matrice de rigidité ne peut pas être inversée, la matrice de rigidité du dernier pas d’itération stable est utilisée. Le calcul se poursuit avec cette matrice jusqu’à ce que la zone de stabilité soit à nouveau atteinte.
Relaxation dynamique
La dernière méthode est adaptée aux calculs selon l’analyse des grandes déformations et à la résolution de problèmes de claquage. Dans cette approche, un paramètre temporel artificiel est introduit. En tenant compte de l’inertie et de l’amortissement, le problème peut alors être traité comme un problème dynamique. Cette approche utilise la méthode d’intégration temporelle explicite ; la matrice de rigidité n’y est pas inversée. Pour un calcul avec relaxation dynamique, aucune partie du modèle ne doit présenter un poids spécifique nul.
Cette méthode inclut également l’amortissement de Rayleigh, qui peut être défini par les constantes α et β selon l’équation suivante avec les dérivées par rapport au temps :
|
M |
Matrice de masse concentrée (diagonale) |
|
C |
Matrice d'amortissement diagonal C = α M + βdiag[K11 ( u ),K22 ( u ),...,Knn ( u )] |
|
K |
Matrice de rigidité |
|
f |
Vecteur des forces externes |
|
u |
Vecteur de déplacement discrétisé |
Éléments de contrôle pour l’analyse non linéaire
Le « nombre maximal d’itérations » détermine combien de cycles de calcul sont au maximum effectués lors d’une analyse selon l’analyse du second ordre ou l’analyse des grandes déformations ainsi que pour les objets à comportement non linéaire. Si le calcul atteint cette limite sans qu’un équilibre ne soit atteint, un message correspondant apparaît. Vous pouvez alors décider si les résultats doivent être affichés.
Le « nombre de pas de charge » est pertinent pour les analyses selon l’analyse du second ordre ou l’analyse des grandes déformations. Lors de la prise en compte des grandes déformations, il est souvent difficile de trouver un équilibre. Les instabilités peuvent être contournées en appliquant la charge en plusieurs étapes. Si vous définissez par exemple deux pas de charge, la moitié de la charge est appliquée lors du premier pas. L’itération se poursuit jusqu’à ce que l’équilibre soit trouvé. Lors du deuxième pas, la charge complète est alors appliquée sur le système déjà déformé et l’itération se poursuit à nouveau jusqu’à l’équilibre.
Options I
Dans cette section, vous pouvez activer différents « réglages spéciaux » pour influencer le calcul selon l’analyse du second ordre ou l’analyse des grandes déformations.
Modifier les paramètres de précision et de tolérance standard
Si vous cochez la case « Modifier les paramètres de précision et de tolérance standard », l’onglet Précision et tolérance est ajouté à la boîte de dialogue. Vous pouvez y ajuster les critères de convergence.
Ignorer toutes les non-linéarités
Avec la case « Ignorer toutes les non-linéarités », vous pouvez désactiver les propriétés non linéaires des éléments pour le calcul. Les tirants, par exemple, restent alors dans le modèle dès que des forces de compression apparaissent. Vous ne devez toutefois supprimer les propriétés non linéaires qu’à des fins de test, par exemple pour trouver la cause d’une instabilité. Parfois, des critères de défaillance mal définis sont responsables de l’interruption du calcul.
Options II
Modifier la charge à l’aide d’un facteur de multiplication
Après avoir coché la case, vous pouvez définir un facteur k par lequel toutes les charges doivent être multipliées.
Dans les anciennes normes, il existe l’exigence de multiplier globalement les charges par un facteur afin d’amplifier les effets selon l’analyse du second ordre pour les analyses de stabilité. La vérification doit quant à elle être effectuée avec les charges d’exploitation. Les deux exigences peuvent être satisfaites en saisissant un facteur supérieur à 1 et en activant la case « Rediviser les résultats par le facteur de charge ».
Pour les analyses selon les normes actuelles, la charge ne doit pas être modifiée à l’aide de facteurs. Il convient plutôt de prendre en compte les facteurs partiels de sécurité et les coefficients de combinaison lors de la superposition dans les situations de projet.
Tenir compte de l’effet de décharge dû aux efforts de traction dans les barres
Les efforts de traction ont un effet de décharge sur un système pré-déformé. La déformation est ainsi réduite et le système stabilisé. Cet effet est généralement exploité lors du calcul selon l’analyse du second ordre et l’analyse des grandes déformations, par exemple pour les halls avec contreventements ou les structures porteuses sollicitées en flexion de manière générale. Pour les poutres sous-tendues, la décharge par traction peut toutefois entraîner dans certaines circonstances une réduction indésirable des déformations et des efforts internes.
Vérification de la stabilité à l’aide du taux de déformation
Si vous cochez la case, RFEM vérifie lors du calcul comment les déformations évoluent au cours des itérations. Si les déplacements ou les rotations augmentent fortement et dépassent une limite interne au programme, le calcul s’interrompt avec un message d’instabilité.
Tenter de calculer une structure instable
Cette case permet de tenter de rendre un modèle instable calculable : RFEM place lors du premier pas de calcul de petits ressorts qui stabilisent le modèle pour la première itération. Après avoir atteint un état initial stable, ces ressorts sont retirés pour les itérations suivantes.
Déplacements dus à la charge de barre de type « Pression interne de tube »
La case est pertinente pour la charge de barre de type pression interne de tube. L’effet dit de Bourdon décrit la tendance d’un tube courbé à se redresser sous l’influence de la pression. Les contraintes circonférentielles et les contraintes axiales résultant de la charge de pression interne conduisent – en tenant compte de la rigidité du matériau et de la déformation transversale – à un allongement axial longitudinal du tube.
Un article technique décrit dans un exemple comment la pression interne des tubes est calculée.
Enregistrer les résultats de tous les pas de charge
Si la charge est appliquée par étapes (voir la section Éléments de contrôle pour l’analyse non linéaire), vous pouvez forcer avec la case la sortie des résultats intermédiaires afin de vérifier les résultats des différents pas de charge.
Solveur d’équations direct asymétrique
Pour un modèle de matériau non linéaire (voir le chapitre Comportement non linéaire du matériau) avec des propriétés asymétriques en traction et en compression, un solveur d’équations direct asymétrique est utilisé. La case offre la possibilité d’utiliser ce solveur d’équations également pour d’autres modèles de matériau, comme par exemple le modèle de matériau « Isotrope non linéaire élastique ».
Équilibre pour la structure non déformée
La case permet d’analyser une structure qui ne se déforme pas – c’est-à-dire un système dont les déformations restent nulles. Cette option d’analyse peut être utile lorsqu’un système est par exemple soumis à une tension en raison d’un cas de charge, tandis que les déformations qui en résultent peuvent être considérées comme atténuées.
Un domaine d’application du calcul de l’équilibre pour la structure non déformée est l’état de contrainte primaire de l’analyse géotechnique. Il s’agit de déterminer, dans le cadre d’un cas de charge ou d’une combinaison de charges, les contraintes résultant de la précharge du sol. Les déformations de ce cas de charge ou de cette combinaison ne présentent toutefois pas d’intérêt et ne font donc pas l’objet d’une utilisation ultérieure.
Paramètres de base
L’onglet Paramètres de base gère les réglages fondamentaux pour le calcul.
Rapport de charge permanente
La case « Déterminer pour les combinaisons de charges » offre la possibilité de déterminer la part d’une charge à effet permanent dans une combinaison de charges. Sélectionnez la combinaison de charges dans la liste ou créez une nouvelle combinaison de charges avec le bouton
. Dans la liste « Comparer la valeur de résultat », vous pouvez ensuite définir quelles parts agissent de manière statique ou variable.
La part de la charge permanente peut être prise en compte conformément aux normes lors de la vérification.
Méthode pour le système d’équations
Les champs de sélection contrôlent quelle méthode est utilisée pour résoudre le système d’équations. Pour éviter tout malentendu : même avec la résolution directe du système d’équations, un calcul itératif a lieu lorsque des non-linéarités sont présentes ou lorsque le calcul est effectué selon l’analyse du second ordre ou l’analyse des grandes déformations. « Direct » et « Itératif » se réfèrent à la gestion des données pendant le calcul.
La méthode de solveur d’équations qui mène plus rapidement à des résultats dépend de la complexité du modèle ainsi que de la taille de la mémoire vive disponible (RAM). Pour les systèmes petits et moyens, la méthode directe est plus efficace.
Pour les systèmes très grands, la méthode itérative mène plus rapidement à des résultats.
Théorie de flexion des plaques
Les surfaces peuvent être calculées selon les théories de flexion de « Mindlin » ou de « Kirchhoff ». Lors du calcul selon Mindlin, les déformations dues à l’effort tranchant sont incluses, selon Kirchhoff, elles ne sont pas prises en compte. L’option de calcul Mindlin convient donc aux plaques et coques relativement épaisses de la construction massive ; l’option Kirchhoff est recommandée pour les surfaces relativement minces comme par exemple les tôles d’acier.
Paramètres pour la méthode itérative
Les cases de cette section sont importantes pour le type d’analyse « Analyse du second ordre (P-Δ) ».
Rapporter les efforts internes à la structure déformée
Les efforts internes des barres sont généralement rapportés à la position modifiée des systèmes de coordonnées de barre, qui existe dans le système déformé. Si la sortie doit être rapportée au système initial non déformé, vous pouvez définir les efforts internes de barre pertinents en désactivant les cases correspondantes.
Part en pourcentage des itérations selon Newton-Raphson combiné avec Picard
La méthode de résolution de Picard part de rigidités sécantes, la méthode de Newton-Raphson de rigidités tangentes. Pour l’option de calcul Newton-Raphson combiné avec Picard, des rigidités sécantes sont utilisées dans les premières itérations, avant que des rigidités tangentes ne soient appliquées pour les itérations restantes. La part des premières itérations avec rigidités sécantes est rapportée au nombre total d’itérations.
Conversion de masse en charge
Les charges peuvent être définies non seulement comme des forces et des moments, mais aussi sous forme de masses. Dans le calcul statique, les masses n’ont toutefois aucun effet. Si elles doivent être prises en compte, activez la case « Masse active ». Indiquez ensuite le « facteur en direction » pour décrire l’effet de la masse. Les masses sont ainsi converties en forces avant le calcul et entrent dans la détermination des efforts internes.
Avec le bouton
, vous pouvez basculer entre la saisie du facteur de masse et la saisie directe de l’accélération. L’étiquetage des champs de saisie est adapté en conséquence.
Réactivation
L’onglet Réactivation est disponible dès qu’une barre avec des propriétés non linéaires existe dans le modèle. Vous pouvez y contrôler comment les barres défaillantes sont traitées lors du calcul.
Les barres défaillantes sont souvent la cause de problèmes d’instabilité, par exemple lorsqu’un modèle de barres est raidi par des tirants. En raison du raccourcissement des montants dû à la charge verticale, les tirants reçoivent lors du premier cycle de calcul de petites forces de compression. Ils sont retirés du système. Au deuxième cycle, le modèle devient instable sans ces tirants. Avec les possibilités de la section « Réactivation des barres défaillantes », vous pouvez tenter d’obtenir un calcul sans message d’erreur.
Vérifier la déformation des barres défaillantes et les réactiver si nécessaire
RFEM analyse à chaque itération les déplacements des nœuds. Si par exemple les extrémités de barre d’un tirant défaillant s’éloignent l’une de l’autre, la barre est à nouveau utilisée dans la matrice de rigidité.
Dans certains cas, la réactivation de barres peut être problématique : une barre est retirée après la première itération, réintroduite après la deuxième itération, retirée à nouveau après la troisième, etc. Le calcul parcourrait cette boucle jusqu’à atteindre le nombre maximal d’itérations possible, sans converger. Le « nombre maximal de réactivations » empêche cet effet. Vous pouvez y définir combien de fois un élément de barre peut être réintroduit avant d’être définitivement retiré de la matrice de rigidité.
Traitement particulier
Si vous cochez la case « Traitement particulier », deux méthodes sont disponibles pour gérer les barres défaillantes. Elles sont combinables avec la réactivation décrite ci-dessus.
- Retirer les barres défaillantes une par une successivement dans les itérations
Après la première itération, par exemple, tous les tirants avec une force de compression ne sont pas retirés en une fois, mais seulement le tirant avec la plus grande force de compression. À la deuxième itération, une seule barre manque alors dans la matrice de rigidité. Ensuite, le tirant avec la plus grande force de compression est à nouveau retiré. De cette manière, le système présente souvent un meilleur comportement de convergence en raison des effets de redistribution.
Cette variante de calcul nécessite plus de temps, car un plus grand nombre d’itérations doit être parcouru. Il faut en outre s’assurer que dans l’onglet « Base », un nombre maximal d’itérations suffisant est prévu.
- Attribuer une très petite rigidité aux barres défaillantes
Les barres défaillantes ne sont pas retirées de la matrice de rigidité, mais une très petite rigidité leur est attribuée. Vous pouvez la définir dans le champ de saisie « Facteur de réduction de la rigidité » : le facteur 1000 signifie que la rigidité de barre est réduite à 1/1000.
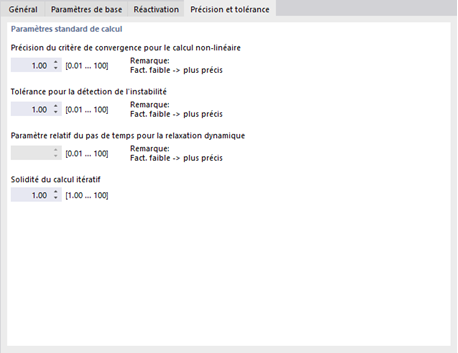
Précision et tolérance
L’onglet Précision et tolérance offre la possibilité d’influencer les paramètres de convergence et de tolérance du calcul. Vous ne devez toutefois modifier les préréglages que dans des cas exceptionnels.
Précision de la limite de convergence pour le calcul non linéaire
Lorsque des effets non linéaires agissent ou que l’analyse est effectuée selon l’analyse du second ordre ou l’analyse des grandes déformations, le calcul peut être influencé par la limite de convergence.
La variation de l’effort normal des deux dernières itérations est comparée barre par barre. Dès que cette variation atteint une certaine fraction de l’effort normal maximal, le calcul se termine. Pendant les itérations, il peut toutefois arriver que les efforts normaux oscillent entre deux valeurs. Vous pouvez empêcher cet effet de pendule en ajustant la « sensibilité ».
La précision influence également le critère de convergence pour les variations de déformation lors du calcul selon l’analyse des grandes déformations, où les non-linéarités géométriques sont prises en compte. Le facteur 1,00 est prédéfini. Le facteur minimal est 0,01, la valeur maximale est 100,00. Plus la valeur est petite, plus le terme de convergence doit être proche du terme de comparaison. La précision des résultats est augmentée en conséquence.
Tolérance pour la détermination de l’instabilité
Il existe différentes approches pour analyser le comportement stabilité d’un modèle. Aucune ne peut toutefois détecter avec une fiabilité absolue les matrices de rigidité singulières.
RFEM utilise deux procédures pour déterminer l’instabilité : d’une part, les éléments de la diagonale principale de la matrice de rigidité sont comparés dans l’absolu toujours avec le même numéro dans les itérations. D’autre part, chaque élément de la diagonale principale est analysé relativement au numéro voisin. La tolérance peut être ajustée dans le champ de saisie. Plus la valeur de tolérance est petite, plus la limite d’instabilité d’un modèle est rapprochée du point d’instabilité exact. La précision des résultats est augmentée en conséquence.
Réglage relatif du pas de temps pour la relaxation dynamique
Le paramètre temporel contrôle le calcul selon la méthode de la relaxation dynamique. Plus la valeur est petite, plus le pas de temps est petit, avec lequel toutes les fluctuations de réponse sont saisies. La précision des résultats est augmentée en conséquence.
Robustesse du calcul itératif
En cas de problèmes de convergence avec la méthode de Newton-Raphson, la robustesse peut être renforcée pour empêcher le « dépassement » de la solution. Avec une réduction de la valeur, le nombre de solutions possibles en présence d’une branche de solution horizontale non convergente et donc la possibilité d’obtenir un résultat valide dans les itérations prescrites sont réduits. Il peut alors être nécessaire d’augmenter le nombre maximal d’itérations.