Le moment d'inertie de l'aire ou moment d'inertie, est une propriété de section utilisée dans les résistances des matériaux. La rigidité d'un composant peut être définie à l'aide du moment d'inertie. Elle est déterminée par la géométrie et la taille de la section.
Le symbole de formule du second moment d'inertie est I et l'unité est mm4, cm4 ou m4 dans le système métrique, ou en4, ft4 ou yd4 dans le système impérial (également ℓ4).
Il existe trois types de moments d'inertie.
Moment quadratique
Les moments d'inertie des aires Iy et Iz décrivent les rigidités en flexion autour des axes locaux y et z. La flèche et les contraintes existantes sont plus faibles dès que le second moment de la surface augmente avec une charge constante. L'axe y est souvent appelé axe « fort », car le second moment de l'aire Iy est plus grand.
|
Iy |
Flächenträgheitsmoment um die y-Achse |
|
z |
Senkrechter Abstand der y-Achse zum Element dA |
|
Iz |
Flächenträgheitsmoment um die z-Achse |
|
y |
Senkrechter Abstand der z-Achse zum Element dA |
Moment biaxial de l'aire
Le moment biaxial de l'aire est souvent appelé moment de centrifugation de l'aire, moment de déviation, moment de déviation de l'aire ou simplement, moment centrifuge. Elle est utilisée pour calculer les déformations sur les sections asymétriques et pour déterminer les charges asymétriques sur les sections quelconques.
Moment d'inertie polaire
Un moment d'inertie, qui décrit la résistance à la torsion d'une section circulaire fermée ou des sections circulaires, est appelé moment d'inertie polaire. Le moment d'inertie polaire Ip est composé des deux moments d'aire Iy et Iz. Il doit également être égal au moment d'inertie de torsion IT pour les sections circulaires et annulaires, qui décrit la rigidité en rotation autour de l'axe longitudinal.
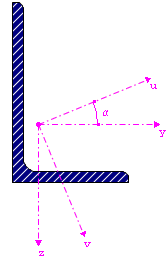
Les moments d’inertie pour les sections non symétriques sont affichés autour des axes principaux u et v de la section.
