momento d'inerzia

Il secondo momento dell'area , noto anche come momento di inerzia dell'area, è una proprietà della sezione trasversale utilizzata nelle resistenze dei materiali. La rigidezza di un componente può essere definita utilizzando il momento di inerzia. È determinato dalla geometria e dalle dimensioni di una sezione trasversale.

Il simbolo della formula del secondo momento dell'area è I e l'unità è mm⁴, cm⁴ o m⁴ nel sistema metrico, o in⁴, ft⁴ o yd⁴ nel sistema imperiale (anche ℓ4).

Esistono tre tipi di momenti secondari dell'area.

Secondo momento assiale dell'area

I secondi momenti assiali dell'area I_y e I_z descrivono le rigidezze contro la flessione attorno agli assi locali y e z. L'inflessione e le tensioni che si verificano sono minori non appena il secondo momento dell'area aumenta con un carico costante. L'asse y è spesso indicato come l'asse "forte", perché il secondo momento dell'area I_y è maggiore qui.

Momento biassiale dell'area

Il momento biassiale dell'area è spesso indicato come momento centrifugo dell'area, momento di deviazione, momento di deviazione dell'area o semplicemente come momento centrifugo. Viene utilizzato per calcolare gli spostamenti generalizzati su sezioni trasversali asimmetriche e per determinare i carichi asimmetrici su qualsiasi sezione trasversale.

Momento di inerzia polare

Un secondo momento di area, che descrive la resistenza di una sezione trasversale circolare chiusa o di sezioni trasversali circolari contro la torsione, è indicato come momento di inerzia polare. Il secondo momento polare di area I_p è composto dai due momenti di area I_y e I_z. Deve anche essere equiparato al momento di inerzia torsionale I_T per sezioni trasversali circolari e circolari, che descrive la rigidezza contro la rotazione attorno all'asse longitudinale.

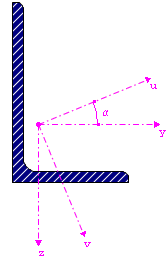
Per le sezioni trasversali asimmetriche, i secondi momenti dell'area sono visualizzati attorno agli assi principali u e v della sezione trasversale.

Figura 2